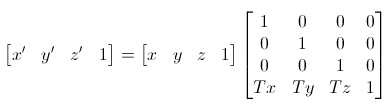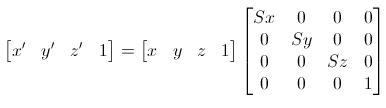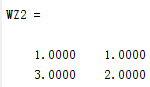十、数字图像处理之几何变换（1）

说明：
几何变换改变了图像中像素间的空间关系，比如可以放大和缩小图像，可以旋转、移动或者扩展图像。几何变换可用于创建小场景，从而适应从某个重放分辨率到另一个分辨率的数字视频，校正由观察几何变换导致的失真，以及排列有相同场景和目标的多幅图像。

前述：几何变换的数学原理

通俗来说，几何变换就是在一个参考坐标系下将物体从一个位置移动到另一个位置的变换。几何变换大致分为：平移变换（Translation），缩放变换（Scaling），旋转变换（Rotation），仿射变换（Affine），投影变换（Projective）。
平移变换

• 平移变换： 将三维空间中的一个点[x, y, z, 1]移动到另外一个点[x’, y’, z’, 1]，三个坐标轴的移动分量分别为dx=Tx, dy=Ty, dz=Tz, 即

  x' = x + Tx
  y' = y + Ty
  z' = z + Tz
  

  矩阵表示式为：
  

• 缩放变换： 将模型放大或者缩小，本质也是对模型上每个顶点进行放大和缩小（顶点坐标值变大或变小），假设变换前的点是[x, y, z, 1]，变换后的点是[x’, y’, z’, 1]，得到

x' = x × Sx
y' = y ×Sy
z' = z× Sz

矩阵表示式为：

• 旋转变换：某个点，在坐标系中的变换为旋转角度为θ，并且逆时针旋转为正；又可以分为绕X轴、Y轴、Z轴或者绕某一个点、某条线旋转，后者需要具体问题具体分析了，并不能给出统一的表达式。
  其矩阵表达式分别为：
  （绕X轴）
  
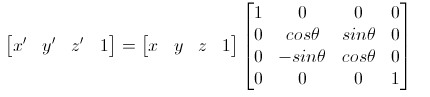
  （绕Y轴）
  
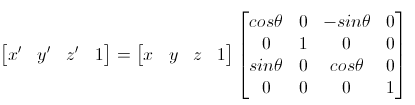
  （绕Z轴）
  

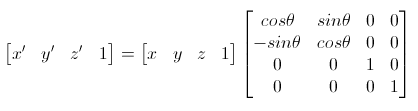
（一）点变换（坐标映射）

（1）概念

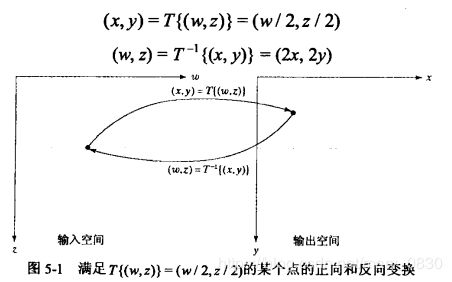
假设（w,z）和（x,y）是两个空间坐标系统，分别表示输入和输出空间。
数学公式：

表示输入空间点到输入空间点的映射。T{·}表示正向变换或正向映射。
其中T^-1{·}表示逆变换或逆映射。

下面借助书上的图更好的理解点变换。

（2）函数maketform

在matlab中我们运用tform结构来描述几何坐标变换，由函数maketform创建，基本语法为：

tform = maketform(transform_type,params,...)

其中，参数transform_type有：‘affine’,‘projective’,‘custom’,‘box’或’composite’。
在本博客中主要“传统”的类型，语法为：

tform = maketform('custom',ndims_in,ndims_out,forward_fcn,inverse_fcn,tdata)

参数forward_fcn和inverse_fcn是正向和反向空间坐标变换的函数句柄，tdata包含前面两个参数所需要的额外信息。

实验一公式及代码：

我们创建两个描述不同空间坐标变换的tform结构，第一个变换用因数3水平地放大，用因数2垂直地放大：

wz = [1 1;8 2];
xy = [2 2;3 1];
tdata = 2;
forward_fcn = @(wz,tdata) [3*wz(:,1),2*wz(:,2)];      %创建正向函数
inverse_fcn = @(xy,tdata) [xy(:,1)/3,xy(:,2)/2];     %创建反向函数
tform1 = maketform('custom',2,2,forward_fcn,inverse_fcn,[]); %创建tform结构
WZ = [1 1;3 2];
XY = tformfwd(WZ,tform1)    %计算正向变换
WZ2 =  tforminv(XY,tform1)    %计算反向变换

实验结果：

上面得到的结果是我们所定义函数所算出的结果，证明上述编写代码的正确性。

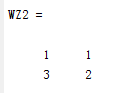
通过WZ2得到的反向变换还原了我们原始数据，证明反向变换代码编写的正确性。

实验二公式及代码：

我们以垂直坐标因子移动水平坐标，垂直坐标不变：

forward_fcn = @(wz,tdata) [wz(:,1)+0.4*wz(:,2),wz(:,2)];
inverse_fcn = @(xy,tdata) [xy(:,1) - 0.4*xy(:,2),xy(:,2)];
tform2 = maketform('custom',2,2,forward_fcn,inverse_fcn,[]);
XY = tformfwd(WZ,tform2)
WZ2 = tforminv(XY,tform2)

实验结果：

下面我自己写两个表达式并编写代码，如下：

实验三公式及代码：

forward_fcn = @(wz,tdata) [wz(:,1)-0.4*wz(:,2),wz(:,2)-0.1*wz(:,1)];
inverse_fcn = @(xy,tdata) [xy(:,1)+0.4*xy(:,2),xy(:,2)+0.1*xy(:,1)];
tform2 = maketform('custom',2,2,forward_fcn,inverse_fcn,[]);
XY = tformfwd(WZ,tform2)
WZ2 = tforminv(XY,tform2)

实验结果如下所示：

（3）函数pointgrid和函数vistform

函数pointgrid

function wz = pointgrid(corners)
[w1,z1] =meshgrid(linspace(corners(1,1),corners(2,1),46),linspace(corners(1),corners(2),10));
[w2,z2] =meshgrid(linspace(linspace(corners(1),corners(2),10),linspace(corners(1),corners(2),46));
wz = [w1(:) z1(:);w2(:) z2(:)];

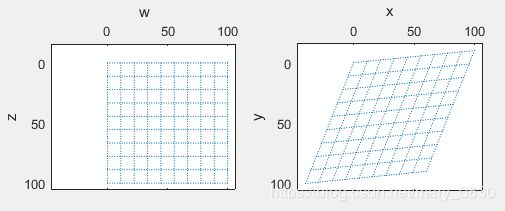
函数vistform

function vistform(tform,wz)
xy = tformfwd(tform,wz);
minlim = min([wz;xy],[],1);
maxlim = max([wz;xy],[],1);
bump = max((maxlim - minlim) * 0.05,0.1);
limits = [minlim(1)-bump(1),maxlim(1)+bump(1),minlim(2)-bump(2),maxlim(2)+bump(2)];
subplot(1,2,1)
grid_plot(wz,limits,'w','z');
subplot(1,2,2)
grid_plot(xy,limits,'x','y');

%————————————————————————————————%
function grid_plot(ab,limits,a_label,b_label)
plot(ab(:,1),ab(:,2),'.','MarkerSize',2)
axis equal,axis ij,axis(limits);
set(gca,'XAxisLocation',top)           %去掉x轴的刻度
xlabel(a_label),ylabel(b_label)

实验代码：

subplot(221),vistform(tform1,pointgrid([0 0;100 100]))
subplot(222),vistform(tform2,pointgrid([0 0;100 100]))

（二）仿射变换

（1）概念

仿射变换的功能是从二维坐标到二维坐标之间的线性变换，且保持二维图形的“平直性”和“平行性”。仿射变换可以通过一系列的原子变换的复合来实现，包括平移，缩放，翻转，旋转和剪切。 通俗来说，仿射变换就是 “线性变换”+“平移”。
对于2D空间，矩阵表达式为：

为了方便，放射变换附加第三坐标的方法写成矩阵相乘形式：

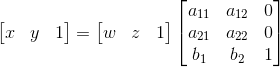
（2）代码

可以用函数maketform创建tform结构：

T = [1 0 0;0.4 1 0;0 0 1];
tform3 = maketform('affine',T);
WZ = [1 1;3 2];
XY = tformfwd(WZ,tform3)

常用的几何变换：

（1）图像剪裁

f= imread('C:\Users\Public\Pictures\Sample Pictures\fengjing3.jpeg');
J = imcrop(f,imrect);

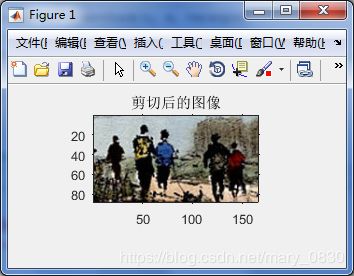
如上图矩形所框选的部分，双击方框，就已经将所选部分保存，再进行下面的显示，得到所选择的图像。

imshow(J),title('剪切后的图像')

（2）图像旋转

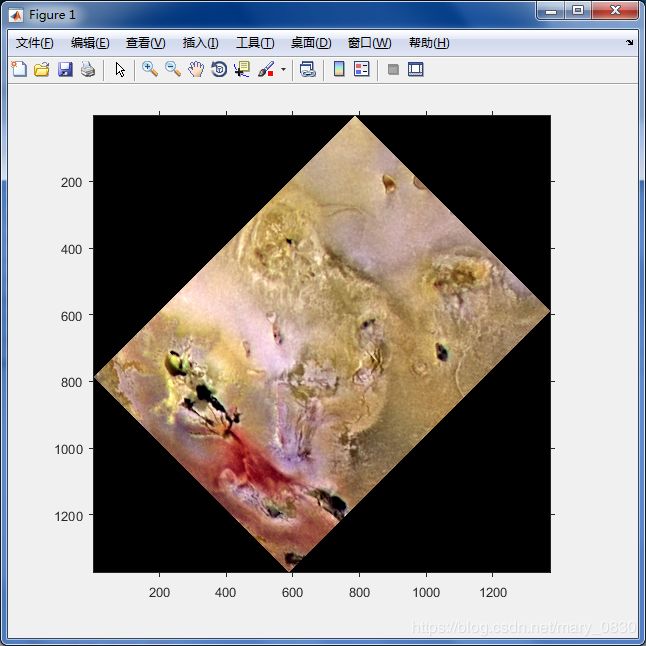
f= imread('C:\Users\Public\Pictures\Sample Pictures\Fig0630(a).tif');
B = imrotate(f,angle,method);    %angle选择45度，method选择'Nearest'（最近邻插值）
imshow(B)

其中，method可以选择’Nearest’、‘Bilinear’、‘Bicubic’，分别是最近邻插值、双线性插值、三次插值。

（3）图像平移

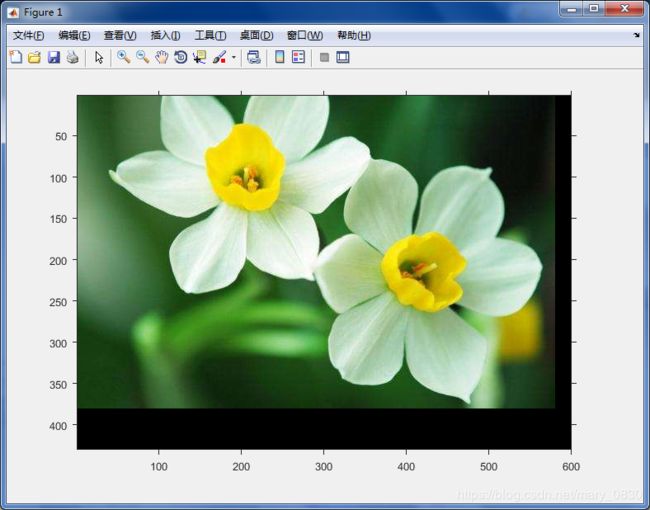
f= imread('C:\Users\Public\Pictures\Sample Pictures\flower.jpg');
C = imtranslate(f,[-20 -50]); 
imshow(C)

（4）图像金字塔缩减和扩展

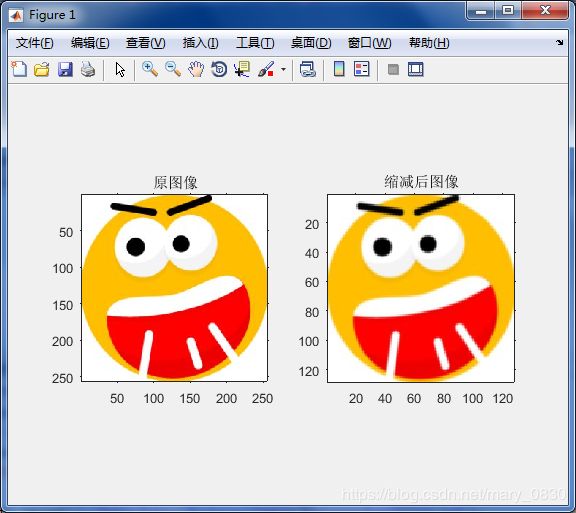
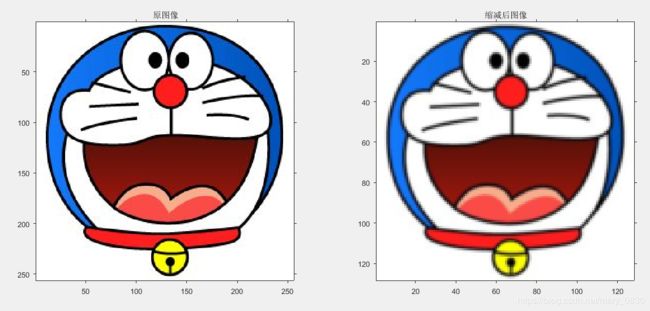
f= imread('C:\Users\Public\Pictures\Sample Pictures\dingdangmao.jpg');
subplot(121),imshow(f),title('原图像')
D = impyramid(f,'reduce');
subplot(122),imshow(D),title('缩减后图像')

其中，direction为 ‘reduce’ 和 ‘expand’ 分别对应着缩减和扩展。

f= imread('C:\Users\Public\Pictures\Sample Pictures\timg.jpg');
subplot(121),imshow(f),title('原图像')
D = impyramid(f,'expand');
subplot(122),imshow(D),title('扩展后图像')

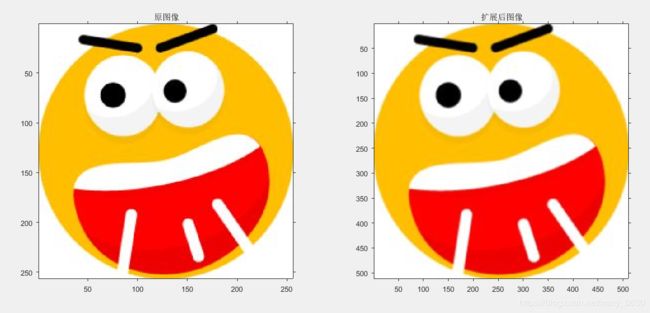
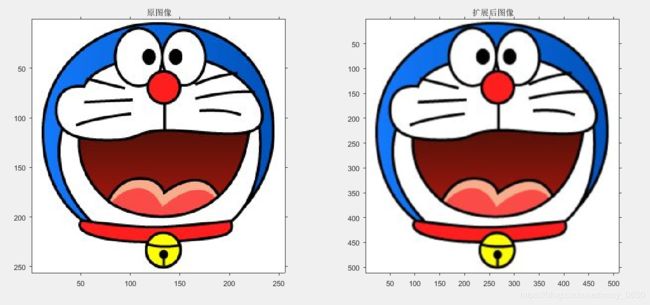实验结论：一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。从实验结果可以得出，当使用图像金字塔的缩减操作时，原始图像是清晰的，会经过操作后变得模糊、边缘产生“锯齿”；当使用扩展操作时，将原图像也变得模糊了，但不同于缩减是，它将原图像是有“锯齿”的变成平滑。

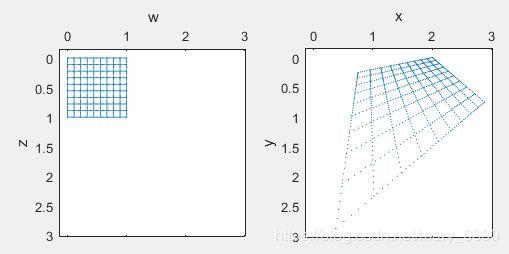
（三）投射变换

这个几何变换与上述所说的仿射投影有一些不同，其辅助坐标不是常量。

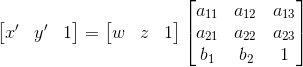
其中，x=x’/h和y=y’/h。在这个变换中，线映射为线，平行线也不再是保持平行。

实验代码如下：

T =[-2.7390 0.2929 -0.6373;0.7426 -0.7500 0.8088;2.8750 0.7500 1.0000];
tform = maketform('projective',T);
vistform(tform,pointgrid([0 0;1 1]));

（四）应用于图像的几何变换

计算公式如下：

在matlab中函数imtransform使用逆映射过程把几何变换应用于图像，基本语法为：

g = imtransform(f,tform)

实验代码：

f =checkerboard(50);
sx = 0.75;
sy = 1.25;
T =[sx 0 0;0 sy 0;0 0 1];
t1 = maketform('affine',T);
g1 = imtransform(f,t1);
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(g1),title('仿射缩放图像');

theta = pi/6;
T2 = [cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0;0 0 1];
t2 = maketform('affine',T2);
g2 = imtransform(f,t2);
imshow(g2),title('旋转后的图像');

T3 = [0.4788 0.0135 -0.0009;0.0135 0.4788 -0.0009;0.5059 0.05059 1.000];
tform3 = maketform('projective',T3);
g3 = imtransform(f,tform3);
imshow(g3),title('投影后的图像');

f= imread('C:\Users\Public\Pictures\Sample Pictures\horse.jpg ');
sx = 0.75;     %设置缩放图像的长
sy = 1.25;    %设置缩放图像的宽
T =[sx 0 0;0 sy 0;0 0 1];      %缩放模板
t1 = maketform('affine',T);
g1 = imtransform(f,t1);
subplot(221),imshow(f),title('原始图像');
subplot(222),imshow(g1),title('仿射缩放图像');
theta = pi/6;     %设置旋转角度
T2 = [cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0;0 0 1];     %旋转模板
t2 = maketform('affine',T2);
g2 = imtransform(f,t2);
subplot(223),imshow(g2),title('旋转后的图像');
T3 = [0.4788 0.0135 -0.0009;0.0135 0.4788 -0.0009;0.5059 0.05059 1.000];
tform3 = maketform('projective',T3);
g3 = imtransform(f,tform3);
subplot(224),imshow(g3),title('投影后的图像');

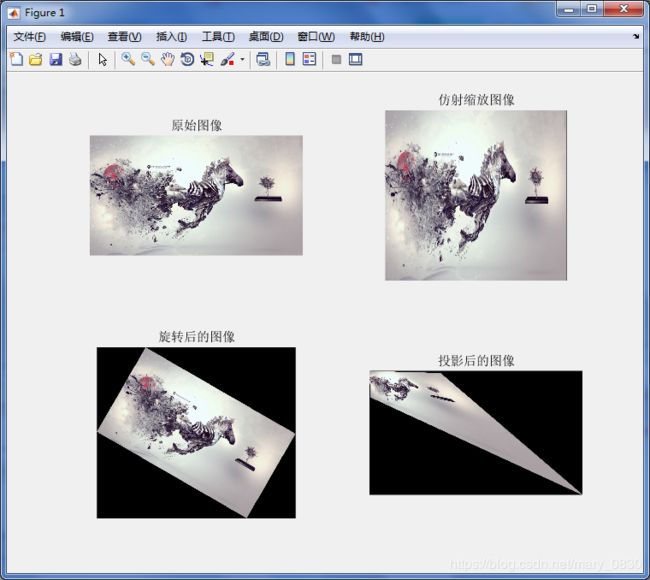
结论： 从上面得到的效果可知，仿射变换从几何直观上说：变换前是直线的，变换后仍然是直线；直线比例保持不变；变换前是原点的，变换后依然是原点。仿射变换就是在原图像的基础上进行缩放、旋转和平移。在图像处理中，当需要进行图像的简单变换时可以采用仿射变换进行处理，以此得到需要得到的效果。