Guava RateLimiter代码梳理（2）预热限流器算法分析

前言

上文针对RateLimiter的基本实现做了一个代码分析，本文将对Guava中另一个RateLimiter实现：带预热功能的SmoothWarmingUp RateLimiter算法和代码做一个简单的分析。使用带预热的限流器的需求是很明显的，如果突发的大量流量到来，在没有预热的情况下，大量请求会打到后台的服务，如果后台服务的缓存陈旧，db和io操作耗时，就有可能会拖垮后台服务，如果有一个预热阶段的话就能够将流量比较平滑的过渡，从而降低后台服务down掉的风险。

变量关系

（这里基本上是翻译的Guava RateLimiter的注释）
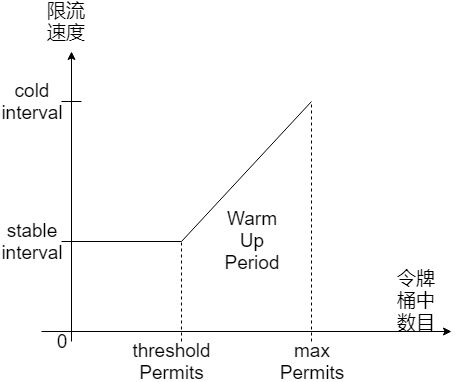
我们首先来看一张图：

算法示意图

有几个变量需要说明：

stableInterval 这个跟之前的文章描述的有点不同，这里考虑是放行令牌桶令牌的速率，类似于漏桶算法
coldInterval 这个是在冷却情况下发放令牌的速率，目前取值为：coldInterval = coldFactor * stableInterval
thresholdPermits 当令牌桶中存储的令牌数目到达阈值时，发放令牌的速率到达稳定
maxPermits 令牌桶中存放令牌的最大数目
warmUpPeriod 预热的时间长度，在这段预热期内令牌桶的存放数目从maxPermits减少到了thresholdPermits

首先我们来明确几个基本点：

限流器的状态（storedPermits）可以视为图中的水平线
当限流器没有流量进来，限流器的状态向右变化（最大到maxPermits）
当限流器发挥功能，它的状态向左变化（最少到0），因为我们本身令牌桶中有storedPermits，我们首先会通过它来获取令牌
如果限流器空闲，那么它将会以一个恒定速率向右变化，变化的速率是maxPermits/warmupPeriod，这样保证了限流器令牌数目从0到maxPermits一共用了warmupPeriod的时长，这里也就隐含了stableInterval * maxPermits = warmupPeriod这一层关系
如果限流器使用中，取得K个令牌的耗时，等于我们上图所示的函数在X个令牌到X-K个令牌之间积分（不要害怕）。举个例子，我们从maxPermits到了thresholdPermits用的时间就是这两个横坐标之间的积分，也就是上图中的梯形区域，这块区域本身就等于warmupPeriod
从thresholdPermits到0所需要的时间是warmupPeriod/2，这里信息量有点大，我们可以算一下：

coldFactor目前写死的3
梯形区域 = 上面的三角形加上下面的矩形
三角形 = （coldInterval - stableInterval）* (maxPermits - thresholdPermits) / 2 = stableInterval * (maxPermits - thresholdPermits)
矩形 = stableInterval * (maxPermits - thresholdPermits) = 三角形区域
由梯形区域 = warmupPeriod 得到 stableInterval * (maxPermits - thresholdPermits ) = warmupPeriod / 2
又由stableInterval * maxPermits = warmupPermits 得到：
stableInterval * thresholdPermits = stableInterval * maxPermits - warmupPeriod / 2 = warmupPeriod / 2
（其实这里已经可以推送出thresholdPermits = maxPermits / 2 了，之前版本的注释其实thresholdPermits 就写的halfPermits，我也不太清楚这里为啥要这么改）

在上面几点的基础上，我们就可以建立各个变量之间的关系了：

已知量：我们创建限流器时预设stableInterval 和warmupPeriod
由thresholdPermits * stableInterval = warmupPeriod / 2推出：thresholdPermits = 0.5 * warmupPeriod / stableInterval
由warmupPeriod = (stableInterval + coldInterval) * (maxPermits - thresholdPermits) / 2 推出（这里就是通过上底加下底乘高除2来得到梯形面积）：maxPermits = thresholdPermits + 2 * warmupPeriod / (stableInterval + coldInterval)

其实你这里把coldInterval = 3 * stableInterval带进去算，你就会发现 2 * thresholdPermits = maxPermits

代码分析

说了这么多，我们再看代码：

     //  初始化设置限流器
    @Override
    void doSetRate(double permitsPerSecond, double stableIntervalMicros) {
      double oldMaxPermits = maxPermits;
      //跟之前部分描述的计算一致
      double coldIntervalMicros = stableIntervalMicros * coldFactor;
      thresholdPermits = 0.5 * warmupPeriodMicros / stableIntervalMicros;
      maxPermits =
          thresholdPermits + 2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros);
      //slop可以看作是梯形斜边的斜率，用于计算threshold到maxPermits之间的限流速率
      slope = (coldIntervalMicros - stableIntervalMicros) / (maxPermits - thresholdPermits);
      if (oldMaxPermits == Double.POSITIVE_INFINITY) {
        // if we don't special-case this, we would get storedPermits == NaN, below
        storedPermits = 0.0;
      } else {
        storedPermits =
            (oldMaxPermits == 0.0)
                ? maxPermits // initial state is cold
                : storedPermits * maxPermits / oldMaxPermits;
      }
    }

初始化的代码跟之前我们描述的计算基本一致。
我们记得之前的文章说过，再调用acquire之后会先调用resync方法去更新桶中的令牌数量：

  void resync(long nowMicros) {
    // if nextFreeTicket is in the past, resync to now
    if (nowMicros > nextFreeTicketMicros) {
      storedPermits = min(maxPermits,
          storedPermits
            + (nowMicros - nextFreeTicketMicros) / coolDownIntervalMicros());
      nextFreeTicketMicros = nowMicros;
    }
  }

在不预热的版本中，coolDownIntervalMicros函数稳定返回stableInterval:

    double coolDownIntervalMicros() {
      return stableIntervalMicros;
    }

而在预热版本中，根据我们之前分析，限流器状态往右运动到maxPermits的速率恒定为maxPermits/warmupPeriod，因此这里
coolDownIntervalMicros函数的实现就应该是：

    double coolDownIntervalMicros() {
      return warmupPeriodMicros / maxPermits;
    }

其实我这里大致算了一下，也就等于stableIntervalMicros了
maxPermits
= thresholdPermits + 2.0 * warmupPeriodMicros / (stableIntervalMicros + coldIntervalMicros);
= 0.5 * warmupPeriod/stableInterval + 2 * warmupPeriod/(stableInterval + 3*stableInterval)
= warmupPeriod/stableInterval
然后再除，就完事儿了

然后我们再来看看计算等待时间的函数：

final long reserveEarliestAvailable(int requiredPermits, long nowMicros) {
    resync(nowMicros);
    long returnValue = nextFreeTicketMicros;
    double storedPermitsToSpend = min(requiredPermits, this.storedPermits);
    double freshPermits = requiredPermits - storedPermitsToSpend;
    long waitMicros = storedPermitsToWaitTime(this.storedPermits, storedPermitsToSpend)
        + (long) (freshPermits * stableIntervalMicros);

    try {
      this.nextFreeTicketMicros = LongMath.checkedAdd(nextFreeTicketMicros, waitMicros);
    } catch (ArithmeticException e) {
      this.nextFreeTicketMicros = Long.MAX_VALUE;
    }
    this.storedPermits -= storedPermitsToSpend;
    return returnValue;
  }

这里基本的功能流程和描述我在之前的文章也已经说明了，这里也不再赘述，大家可以看到真正有变化的就是在这一行

long waitMicros = storedPermitsToWaitTime(this.storedPermits, storedPermitsToSpend)

这一行计算了消费令牌桶中storedPermits需要的时间，我们知道再不预热的版本中这里是直接返回了0，那么在预热的版本中应该是怎样的呢？

    long storedPermitsToWaitTime(double storedPermits, double permitsToTake) {
      //在阈值以上可用的令牌数目
      double availablePermitsAboveThreshold = storedPermits - thresholdPermits;
      long micros = 0;
      // measuring the integral on the right part of the function (the climbing line)
      //计算右边梯形区域的积分（面积）
      if (availablePermitsAboveThreshold > 0.0) {
        //计算在阈值以上能拿的令牌数目
        double permitsAboveThresholdToTake = min(availablePermitsAboveThreshold, permitsToTake);
        //梯形高:permitsAboveThresholdToTake
        //梯形下底:permitsToTime(availablePermitsAboveThreshold)
        //梯形上帝:permitsToTime(availablePermitsAboveThreshold - permitsAboveThresholdToTake)
        micros = (long) (permitsAboveThresholdToTake
            * (permitsToTime(availablePermitsAboveThreshold)
            + permitsToTime(availablePermitsAboveThreshold - permitsAboveThresholdToTake)) / 2.0);
        permitsToTake -= permitsAboveThresholdToTake;
      }
      // measuring the integral on the left part of the function (the horizontal line)
      // 加上示意图左边的矩形区域，即放行速率稳定在stableInterval
      micros += (stableIntervalMicros * permitsToTake);
      return micros;
    }
    //根据slop和stableIntervalMicros计算放行的时间
    //可以想象计算出的结果为梯形斜边上的某个点
    private double permitsToTime(double permits) {
      return stableIntervalMicros + permits * slope;
    }

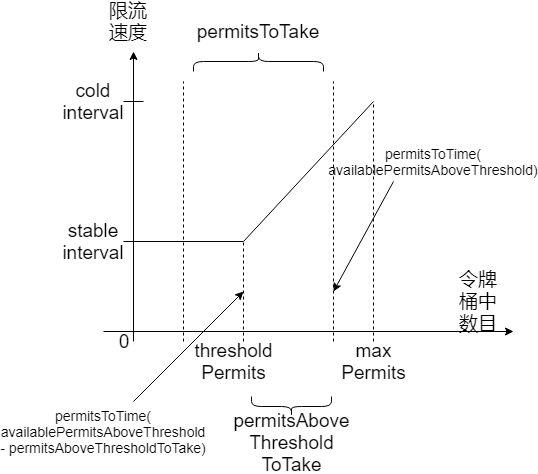
上面代码计算出了获取storedPermits需要的时间长度。可能代码和注释大家看起来比较模糊，我这里也用图来说明:

storedPermits获取时间计算

测试

测试代码如下：

/**
 * @author: Yuanqing Luo
 * @date: 2018/11/13
 **/
public class GuavaWarmupDemo {

    public static void main(String[] args){
        RateLimiter limiter = RateLimiter.create(5, 2, TimeUnit.SECONDS);
        ExecutorService executorService = Executors.newFixedThreadPool(2);
        final long start = System.currentTimeMillis();
        for(int i=2;i>0;i--){
            executorService.submit(() -> {
                int round = 5;
                while(round-- > 0){
                    limiter.acquire();
                    try {
                        Thread.sleep(300);
                    } catch (InterruptedException e) {
                        e.printStackTrace();
                    }
                    System.out.println("time:" + (System.currentTimeMillis() - start));
                }

            });
        }

    }
}

得到的结果

time:411
time:964
time:1454
time:1841
time:2162
time:2399
time:2615
time:2801
time:3000
time:3200

可以看到，最开始获取令牌的时间在450ms左右，此时属于预热阶段，到第5次之后慢慢稳定到了200ms，这与我们在之前设置的QPS=5是一致的。证实了这个算法的有效性

结语

这篇文章作为之前Guava RateLimiter的补充，解释了Guava中预热的限流器的算法与工作方式。最后发现，还是要学好数学呀。

Guava RateLimiter代码梳理（2）预热限流器算法分析

前言

变量关系

代码分析

测试

结语

你可能感兴趣的:(Guava RateLimiter代码梳理（2）预热限流器算法分析)