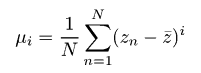扫描探针显微镜AFM，MFM，STM，SNOM / NSOM数据可视化和分析软件

Gwyddion

http://gwyddion.net/

Gwyddion是用于SPM（扫描探针显微镜）数据可视化和分析的模块化程序。主要用于分析通过扫描探针显微镜技术（AFM，MFM，STM，SNOM / NSOM）获得的高度场，并且它支持 许多SPM数据格式。然而，它可以用于一般高度场和（灰度）图像处理，例如用于分析轮廓测量数据或来自成像分光光度法的厚度图。

Gwyddion提供大量 数据处理功能，包括所有标准统计表征，调平和数据校正，过滤或纹理标记功能。由于开发人员是活跃的SPM用户，该程序还包含许多他们认为有用的特定，不常见，奇数和实验数据处理方法 - 您可能会发现它们也很有用。

Gwyddion是免费和开源软件，由GNU通用公共许可证涵盖 。它旨在提供用于2D数据处理和分析的模块化程序，可以通过第三方模块和脚本轻松扩展。此外，由于它是免费软件，它为开发人员和用户提供源代码，这使得更容易验证其数据处理算法和进一步的程序改进。

Gwyddion在常见架构上运行GNU / Linux，Microsoft Windows，Mac OS X和FreeBSD操作系统。所有系统也可用于开发。它具有基于广泛可移植的Gtk +工具包的现代图形用户界面，在所有支持的系统中保持一致。

 

统计分析

在分析随机粗糙表面时，我们通常需要统计方法来确定一组代表性数值。在Gwyddion中，有几种方法可以做到这一点。在本节中，我们将解释Gwyddion中提供的各种统计工具和模块，并介绍用于开发它们所使用的算法的基本方程式。

扫描探针显微镜数据通常表示为大小为N×M的二维数据字段，其中 N和M 分别是数据字段的行数和列数。该场的实际区域表示为 L x × L y ，其中L x和L y 是沿各自轴的尺寸。采样间隔（扫描内两个相邻点之间的距离）表示为 Δ。我们假设x和 y的采样间隔相同，给定点（x，  y）处的表面高度可以通过给出统计特性的随机函数ξ（x，  y）来描述。

注意，AFM数据通常被收集为沿x轴的线扫描 ，它们被连接在一起以形成二维图像。因此， x方向上的扫描速度显着高于y方向上的扫描速度。结果，AFM数据的统计特性通常沿x轮廓收集，因为它们受样品的低频噪声和热漂移的影响较小。

统计数量工具 

统计量包括高度值分布的基本属性，例如方差，偏度和峰度。通过统计数量工具在Gwyddion中可访问的数值分为几组。

基于矩

基于力矩的量使用具有一些高度幂的高度分布函数的积分来表示。它们包括熟悉的数量：

• 平均值。
• 均方粗糙度或高度不规则的RMS S q：该数量是从数据值的第二中心矩计算的。
• 只有在使用掩蔽时，Grain-wise粒度RMS值才与普通RMS不同。然后分别为每个颗粒（掩模或倒置掩模的连续部分，取决于掩蔽类型）确定平均值，然后从这些每颗粒平均值计算方差。
• 平均粗糙度或S a高度不规则的值。
• 根据数据值的第3个中心矩计算出的高度分布偏度。
• 高度分布峰度从数据值的第4个中心矩计算。

更精确地，RMS（σ），偏度（γ 1）和峰度（γ 2）从的中心矩计算i个顺序 μ i

其中z̄表示平均值。由以下公式表示：

请注意，Gwyddion计算过度峰度，高斯数据分布为零。添加3以获得区域纹理参数Sku。

平均粗糙度S a类似于RMS值，差异在于它是根据与平均值的数据差异的绝对值之和而不是它们的平方来计算的。

 

统计函数工具 

可以使用统计函数工具访问一维统计函数 。在工具窗口中，您可以使用左侧标记为“ 输出类型”的选择框选择要评估的函数。图表预览将自动更新。您可以选择评估的方向（水平或垂直），但如上所述，我们建议使用快速扫描轴方向。您还可以选择 要使用的插值方法。完成后，单击“ 应用”关闭工具窗口并输出包含统计数据的新图形窗口。

提示

与统计数量 工具类似 ，默认情况下，此工具会评估整个图像，但您可以根据需要选择要分析的子区域。

自相关函数

自相关函数由下式给出

其中z 1和 z 2是点（x 1，y 1）， （x 2，y 2）处的高度值 ; 此外， τ X  =  X 1  -  X 2和 τ ÿ  =  ý 1  -  ý 2。函数w（z 1， z 2， τ X， τ ÿ） 表示随机函数的二维概率密度 ξ（X，  ÿ）对应于点 （X 1，ÿ 1）， （X 2，ÿ 2），并且这些点之间的距离τ。

从离散的AFM数据可以将此函数评估为

其中m =  τ X /Δ X， Ñ  =  τ ý /Δ ÿ。该函数可以因此一组离散的值来评价 τ X和 τ ÿ由采样间隔分隔 Δ X和 Δ ÿ分别。

对于AFM测量，我们通常仅基于沿快扫描轴的轮廓来评估一维自相关函数。因此，可以从离散AFM数据值评估为

 

通常假设一维自相关函数具有高斯的形式，即它可以由以下关系给出

其中σ表示高度的均方根偏差，T 表示自相关长度。

对于指数自相关函数，我们有以下关系

 

与模拟的高斯随机粗糙表面而获得（即，具有高斯自相关函数）的自相关函数σ  ≈20纳米和 Ť  ≈300纳米。

我们还可以引入径向ACF G r（τ），即角度平均的二维ACF，其当然包含与各向同性表面的一维ACF相同的信息：