Ternary Search Trees 三分树

Efficient auto-complete with a ternary search tree

分类： 算法和数据结构学习 2012-04-18 18:03  125人阅读  评论(0)  收藏  举报

search tree pointers structure character string

目录(?)[+]

Over the past couple of years, auto-complete has popped up all over the web. Facebook, YouTube, Google, Bing, MSDN, LinkedIn and lots of other websites all try to complete your phrase as soon as you start typing.

Auto-complete definitely makes for a nice user experience, but it can be a challenge to implement efficiently. In many cases, an efficient implementation requires the use of interesting algorithms and data structures. In this blog post, I will describe one simple data structure that can be used to implement auto-complete: a ternary search tree.

Trie: simple but space-inefficient

Before discussing ternary search trees, let’s take a look at a simple data structure that supports a fast auto-complete lookup but needs too much memory: a trie. A trie is a tree-like data structure in which each node contains an array of pointers, one pointer for each character in the alphabet. Starting at the root node, we can trace a word by following pointers corresponding to the letters in the target word.

Each node could be implemented like this in C#:

class TrieNode
{
    public const int ALPHABET_SIZE = 26;
    public TrieNode[] m_pointers = new TrieNode[ALPHABET_SIZE];
    public bool m_endsString = false;
}

Here is a trie that stores words AB, ABBA, ABCD, and BCD. Nodes that terminate words are marked yellow:

 

 

Implementing auto complete using a trie is easy. We simply trace pointers to get to a node that represents the string the user entered. By exploring the trie from that node down, we can enumerate all strings that complete user’s input.

But, a trie has a major problem that you can see in the diagram above. The diagram only fits on the page because the trie only supports four letters {A,B,C,D}. If we needed to support all 26 English letters, each node would have to store 26 pointers. And, if we need to support international characters, punctuation, or distinguish between lowercase and uppercase characters, the memory usage grows becomes untenable.

Our problem has to do with the memory taken up by all the null pointers stored in the node arrays. We could consider using a different data structure in each node, such as a hash map. However, managing thousands and thousands of hash maps is generally not a good idea, so let’s take a look at a better solution.

Ternary search tree to the rescue

A ternary tree is a data structure that solves the memory problem of tries in a more clever way. To avoid the memory occupied by unnecessary pointers, each trie node is represented as a tree-within-a-tree rather than as an array. Each non-null pointer in the trie node gets its own node in a ternary search tree.

For example, the trie from the example above would be represented in the following way as a ternary search tree:

The ternary search tree contains three types of arrows. First, there are arrows that correspond to arrows in the corresponding trie, shown as dashed down-arrows. Traversing a down-arrow corresponds to “matching” the character from which the arrow starts. The left- and right- arrow are traversed when the current character does not match the desired character at the current position. We take the left-arrow if the character we are looking for is alphabetically before the character in the current node, and the right-arrow in the opposite case.

For example, green arrows show how we’d confirm that the ternary tree contains string ABBA:

 

And this is how we’d find that the ternary string does not contain string ABD:

 

Ternary search tree on a server

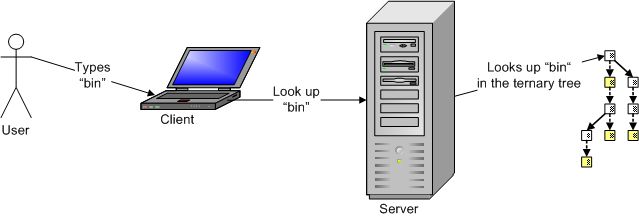
On the web, a significant chunk of the auto-complete work has to be done by the server. Often, the set of possible completions is large, so it is usually not a good idea to download all of it to the client. Instead, the ternary tree is stored on the server, and the client will send prefix queries to the server.

The client will send a query for words starting with “bin” to the server:

  

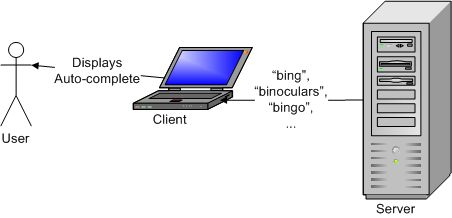
And the server responds with a list of possible words:

 

Implementation

Here is a simple ternary search tree implementation in C#:

public class TernaryTree
{
    private Node m_root = null;

    private void Add(string s, int pos, ref Node node)
    {
        if (node == null) { node = new Node(s[pos], false); }

        if (s[pos] < node.m_char) { Add(s, pos, ref node.m_left); }
        else if (s[pos] > node.m_char) { Add(s, pos, ref node.m_right); }
        else
        {
            if (pos + 1 == s.Length) { node.m_wordEnd = true; }
            else { Add(s, pos + 1, ref node.m_center); }
        }
    }

    public void Add(string s)
    {
        if (s == null || s == "") throw new ArgumentException();

        Add(s, 0, ref m_root);
    }

    public bool Contains(string s)
    {
        if (s == null || s == "") throw new ArgumentException();

        int pos = 0;
        Node node = m_root;
        while (node != null)
        {
            int cmp = s[pos] - node.m_char;
            if (s[pos] < node.m_char) { node = node.m_left; }
            else if (s[pos] > node.m_char) { node = node.m_right; }
            else
            {
                if (++pos == s.Length) return node.m_wordEnd;
                node = node.m_center;
            }
        }

        return false;
    }
}

And here is the Node class:

class Node
{
    internal char m_char;
    internal Node m_left, m_center, m_right;
    internal bool m_wordEnd;

    public Node(char ch, bool wordEnd)
    {
        m_char = ch;
        m_wordEnd = wordEnd;
    }
}

Remarks

For best performance, strings should be inserted into the ternary tree in a random order. In particular, do not insert strings in the alphabetical order. Each mini-tree that corresponds to a single trie node would degenerate into a linked list, significantly increasing the cost of lookups. Of course, more complex self-balancing ternary trees can be implemented as well.

And, don’t use a fancier data structure than you have to. If you only have a relatively small set of candidate words (say on the order of hundreds) a brute-force search should be fast enough.

Further reading

Another article on tries is available on DDJ (careful, their implementation assumes that no word is a prefix of another):

http://www.ddj.com/windows/184410528

If you like this article, also check out these posts on my blog:

• Skip lists are fascinating!
• Numbers that cannot be computed
• Quicksort killer

Ternary Search Trees 三分树

By admin|algorithm, c|Be the first to comment!

经常碰到要存一堆的string, 这个时候可以用hash tables, 虽然hash tables 查找很快,但是hash tables不能表现出字符串之间的联系.可以用binary search tree, 但是查询速度不是很理想. 可以用trie, 不过trie会浪费很多空间(当然你也可以用二个数组实现也比较省空间). 所以这里Ternary Search trees 有trie的查询速度快的优点,以及binary search tree省空间的优点.

实现一个12个单词的查找

这个是用二分查找树实现,n是单词个数,len是长度,复杂度是O(logn * n),空间是n*len

这个是用trie实现,复杂度O(n), 空间是 这里是18 * 26(假设只有26个小写字符),随着单词长度的增长等,需要的空间就更多

这个是Ternary search tree, 可以看出空间复杂度和binary search tree 一样, 复杂度近似O(n),常数上会比trie差点.

介绍

Ternary search tree 有binary search tree 省空间和trie 查询快的优点.
Ternary search tree 有三个只节点,在查找的时候,比较当前字符,如果查找的字符比较小,那么就跳到左节点.如果查找的字符比较大,那么就跳转到友节点.如果这个字符正好相等,那么就走向中间节点.这个时候比较下一个字符.
比如上面的例子,要查找”ax”, 先比较”a” 和 “i”, “a” < "i",跳转到"i"的左节点, 比较 "a" < "b", 跳转到"b"的左节点, "a" = "a", 跳转到 "a"的中间节点,并且比较下一个字符"x". "x" > “s” , 跳转到”s” 的右节点, 比较 “x” > “t” 发现”t” 没有右节点了.找出结果,不存在”ax”这个字符

构造方法

这里用c语言来实现
节点定义:

typedef  struct tnode  *Tptr ;
typedef  struct tnode  {
     char s ;
    Tptr lokid , eqkid , hikid ;
} Tnode ;

先介绍查找的方法:

int search ( char  *s )  // s是想要查找的字符串
{
    Tptr p ;
    p  = t ;  //t 是已经构造好的Ternary search tree 的root 节点.
     while  (p )  {
         if  ( *s  < p ->s )  {  // 如果*s 比 p->s 小, 那么节点跳到p->lokid
            p  = p ->lokid ;
         }  else  if  ( *s  > p ->s )  {
            p  = p ->hikid ;
         }  else  {
             if  ( * (s )  ==  '\0' )  {  //当*s 是'\0'时候,则查找成功
                 return  1 ;
             }  //如果*s == p->s,走向中间节点,并且s++
            s ++;
            p  = p ->eqkid ;
         }
     }
     return  0 ;
}

插入某一个字符串:

Tptr insert (Tptr p ,  char  *s )
{
     if  (p  == NULL )  {
        p  =  (Tptr ) malloc ( sizeof (Tnode ) ) ;
        p ->s  =  *s ;
        p ->lokid  = p ->eqkid  = p ->hikid  = NULL ;
     }
     if  ( *s  < p ->s )  {
        p ->lokid  = insert (p ->lokid , s ) ;
     }  else  if  ( *s  > p ->s )  {
        p ->hikid  = insert (p ->hikid , s ) ;
     }  else  {
         if  ( *s  !=  '\0' )  {
            p ->eqkid  = insert (p ->eqkid ,  ++s ) ;
         }  else  {
            p ->eqkid  =  (Tptr ) insertstr ;  //insertstr 是要插入的字符串,方便遍历所有字符串等操作
         }
     }
     return p ;
}

同binary search tree 一样,插入的顺序也是讲究的,binary search tree 在最坏情况下顺序插入字符串会退化成一个链表.不过Ternary search Tree 最坏情况会比 binary search tree 好很多.

肯定得有一个遍历某一个树的操作

//这里以字典序输出所有的字符串
void traverse (Tptr p )  //这里遍历某一个节点以下的所有节点,如果是非根节点,则是有同一个前缀的字符串
{ 
     if  ( !p )  return ; 
    traverse (p ->lokid ) ; 
     if  (p ->s  !=  '\0' )  { 
        traverse (p ->eqkid ) ; 
     }  else  { 
         printf ( "%s\n" ,  ( char  * )p ->eqkid ) ; 
     } 
    traverse (p ->hikid ) ; 
}

应用

这里先介绍两个应用,一个是模糊查询,一个是找出包含公共前缀的字符串, 一个是相邻查询(哈密顿距离小于某个范围)
模糊查询
psearch(“root”, “.a.a.a”) 应该能匹配出baxaca, cadakd 等字符串

void psearch1 (Tptr p ,  char  *s )
{
     if  (p  == NULL )  {
         return  ;
     }
     if  ( *s  ==  '.'  ||  *s  < p ->s )  {  //如果*s 是'.' 或者 *s < p->s 就查找左子树
        psearch1 (p ->lokid , s ) ; 
     }
     if  ( *s  ==  '.'  ||  *s  > p ->s )  {  //同上
        psearch1 (p ->hikid , s ) ; 
     }
     if  ( *s  ==  '.'  ||  *s  == p ->s )  {  // *s = '.' 或者 *s == p->s 则去查找下一个字符
         if  ( *s  && p ->s  && p ->eqkid  != NULL )  { 
            psearch1 (p ->eqkid , s  +  1 ) ;
         }
     }
     if  ( *s  ==  '\0'  && p ->s  ==  '\0' )  {
         printf ( "%s\n" ,  ( char  * ) p ->eqkid ) ;
     }
}

解决在哈密顿距离内的匹配问题,比如hobby和dobbd,hocbe的哈密顿距离都是2

void nearsearch (Tptr p ,  char  *s ,  int d )  //s 是要查找的字符串, d是哈密顿距离
{
     if  (p  == NULL  || d  <  0 )
         return  ;
     if  (d  >  0  ||  *s  < p ->s )  {
            nearsearch (p ->lokid , s , d ) ;
     }
     if  (d  >  0  ||  *s  > p ->s )  {
            nearsearch (p ->hikid , s , d ) ;
     }
     if  (p ->s  ==  '\0' )  {
         if  ( ( int ) strlen (s )  <= d )  {
             printf ( "%s\n" ,  ( char  * ) p ->eqkid ) ;
         }
     }  else  {
        nearsearch (p ->eqkid ,  *s  ? s  +  1  : s ,  ( *s  == p ->s )  ? d  : d  -  1 ) ;
     }   
}

搜索引擎输入bin, 然后相应的找出所有以bin开头的前缀匹配这样类似的结果.比如bing,binha,binb 就是找出所有前缀匹配的结果.

void presearch (Tptr p ,  char  *s )  //s 是想要找的前缀
{
     if  (p  == NULL )
         return ;
     if  ( *s  < p ->s )  {
        presearch (p ->lokid , s ) ;
     }  else  if  ( *s  > p ->s )  {
        presearch (p ->hikid , s ) ;
     }  else  {
         if  ( * (s  +  1 )  ==  '\0' )  {
            traverse (p ->eqkid ) ;  // 遍历这个节点,也就是找出包含这个节点的所有字符
             return  ;
         }  else  {
            presearch (p ->eqkid , s  +  1 ) ;
         }
     }
}

总结

1.Ternary search tree 效率高而且容易实现
2.Ternary search tree 大体上效率比hash来的快,因为当数据量大的时候hash出现碰撞的几率也会大,而Ternary search tree 是指数增长
3.Ternary search tree 增长和收缩很方便,而 hash改变大小的话则需要拷贝内存重新hash等操作
4.Ternary search tree 支持模糊匹配,哈密顿距离查找,前缀查找等操作
5.Ternary search tree 支持许多其他操作,比如字典序输出所有字符串等,trie也能做,不过很费时.

参考:http://drdobbs.com/database/184410528?pgno=1