LeetCode Weekly Contest 127
第一次参加 LeetCode 的每周编程赛,排在 178 / 4682 ,还是可以接受的。(第一题交了次错答案罚时 5分钟真的伤不起啊不然都可以挺进前100了)
1、1005. Maximize Sum Of Array After K Negations
Given an array A of integers, we must modify the array in the following way: we choose an i and replace A[i] with -A[i], and we repeat this process K times in total. (We may choose the same index i multiple times.)
Return the largest possible sum of the array after modifying it in this way.
Example 1:
Input: A = [4,2,3], K = 1
Output: 5
Explanation: Choose indices (1,) and A becomes [4,-2,3].
题意
一个数组,进行 K 次操作(一次操作是对某个数正负取反,可以对同一个数进行操作),求操作后数组和的最大值。
解题思路
贪心法,对数组排序,先只对负数操作,从最小的开始。全操作完之后,如果K不剩,直接返回和;如果K还剩,说明此时已经全部转化为正数,那么对最小的正数操作。判断一下 K 是否是2的倍数来决定是否操作。
class Solution:
def largestSumAfterKNegations(self, A: List[int], K: int) -> int:
A.sort() # 排序
target = -1
for i, ele in enumerate(A):
if K and ele < 0:
A[i] = -A[i]
target = i
K -= 1
else:
break
K = K % 2
if K > 0: # 需要对最小的正数取反,找到最小的正数
if target+1<len(A) and A[target]>A[target+1]:
A[target+1] = -A[target+1]
else:
A[target] = -A[target]
return sum(A)
2、1006. Clumsy Factorial
Normally, the factorial of a positive integer n is the product of all positive integers less than or equal to n. For example, factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1.
We instead make a clumsy factorial: using the integers in decreasing order, we swap out the multiply operations for a fixed rotation of operations: multiply (*), divide (/), add (+) and subtract (-) in this order.
For example, clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1. However, these operations are still applied using the usual order of operations of arithmetic: we do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that 10 * 9 / 8 equals 11. This guarantees the result is an integer.
Implement the clumsy function as defined above: given an integer N, it returns the clumsy factorial of N.
Example 1:
Input: 4
Output: 7
Explanation: 7 = 4 * 3 / 2 + 1
题意
定义一个新的阶乘运算,依次使用 + - * / 几个符号,求最后结果。
解题思路
直接模拟这个运算,除了遇到减法要考虑到后面三个数字县做运算,其余符号直接按从左到右的顺序来计算即可。
class Solution:
import math
def clumsy(self, N: int) -> int:
oper = 0
ret = N
N -= 1
while N >= 1: # N是当前要处理的数
if oper == 0: # *
ret *= N
oper = (oper+1)%4
N -= 1
elif oper == 1: # /
ret = math.floor(ret/N)
oper = (oper+1)%4
N -= 1
elif oper == 2: # +
ret += N
oper = (oper+1)%4
N -= 1
else: # -
if N >= 3:
ret -= (math.floor(N*(N-1)/(N-2)))
N -= 3
oper = 2 # 运算符变成 +
elif N == 2:
ret -= 2
return ret
elif N == 1:
ret -= 1
return ret
return ret
3、1007. Minimum Domino Rotations For Equal Row
In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the i-th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the i-th domino, so that A[i] and B[i] swap values.
Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.
If it cannot be done, return -1.
Example 1:
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
题意
两行数组,至少交换多少次,可以使得上面一行数组或下面的数组一行内内元素全相等。
解题思路
直接暴力枚举。假设最后调整之后一行内元素全为 K,枚举数组A的每个元素作为这个K的可能值,判断AB对应位置是否等于K来判断是否要进行交换操作。加入visit数组去重,加快查找速度。
class Solution:
def minDominoRotations(self, A: List[int], B: List[int]) -> int:
def tryswap(A, B):
visit = []
n = len(A)
minSwapNum = 99999
for i,ele in enumerate(A):
if ele in visit:
continue
visit.append(ele) # 假设它是最后转化的结果
swapNum = 0
for j in range(n):
if A[j] == ele:
continue
elif B[j] == ele:
swapNum += 1
else:
swapNum = 99999
break
minSwapNum = min(minSwapNum, swapNum)
return minSwapNum
swapNum = min(tryswap(A, B), tryswap(B, A))
if swapNum == 99999:
return -1
return swapNum
4、1008. Construct Binary Search Tree from Preorder Traversal
Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traversesnode.left, then traverses node.right.)
Example 1:
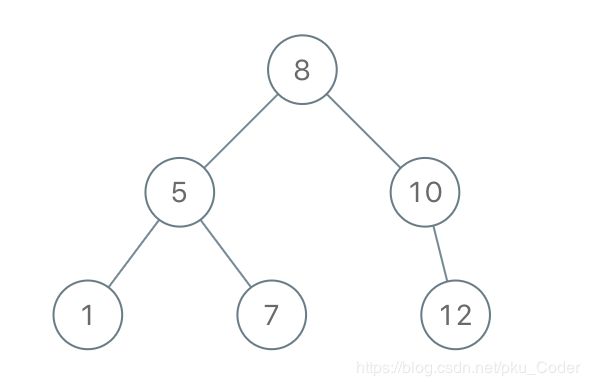
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
题意
根据先序序列重建二叉搜索树。
解题思路
先序序列第一个元素肯定是根节点。然后向后找到第一个大于它的元素的位置为K,那么list[1:K]是它的左子树,list[K:]是它的右子树,递归建树。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
if len(preorder)==0:
return None
root = TreeNode(preorder[0])
target = len(preorder)
for i,ele in enumerate(preorder):
if ele > preorder[0]:
target = i
break
root.left = self.bstFromPreorder(preorder[1:target])
root.right = self.bstFromPreorder(preorder[target:])
return root