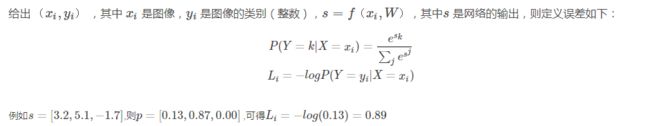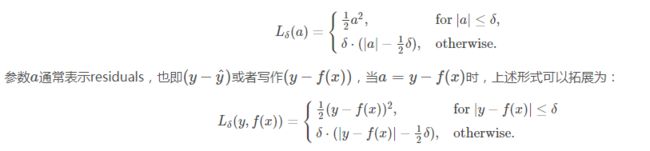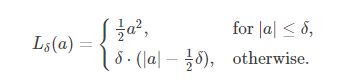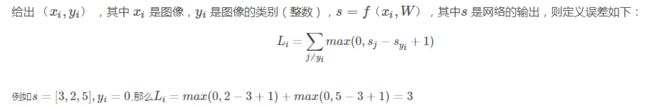深度学习论文中常见loss函数汇总（tensorflow代码实现）

 

1、Softmax交叉熵损失函数（多分类）

参考

（1）定义

def get_softmax_loss(features,one_hot_labels):
    prob = tf.nn.softmax(features + 1e-5)
    cross_entropy = tf.multiply(one_hot_labels,tf.log(tf.clip_by_value(prob,1e-5,1.0)))
    #tf.clip_by_value(A, min, max)：输入一个张量A，把A中的每一个元素的值都压缩在min和max之间。小
    #于min的让它等于min，大于max的元素的值等于max。
    loss = -tf.reduce_mean(cross_entropy)
    return loss

（2）多分类问题的 softmax loss 和二分类问题的 logistic 回归的 loss
         二分类问题的logistic回归的loss函数是：

        
        可以看出，二类别的分类是多分类的一个特殊情况，因此也可以用softmax的方式来处理。但是二分类又是一个特例，因为它的类别不用写成one-hot vector，而是直接用0到1之间的一个数字就可以表示，接近1就是正例，接近0就是反例。所以符合上面的这个公式。这个公式可以看出，y=0，即真实标签为0的时候，第一项就没有了，loss变成-(1-y)ln(1-a)，也就是-ln(1-a)，a越接近0，loss越小；y=1时反之，这样就使得a越来越趋近于真实答案。

2、Center loss

参考

def get_center_loss(features, labels, alpha, num_classes):
    # alpha:中心的更新比例
    # 获取特征长度
    len_features = features.get_shape()[1]
    # 建立一个变量，存储每一类的中心，不训练
    centers = tf.get_variable('centers', [num_classes, len_features], dtype=tf.float32,
        initializer=tf.constant_initializer(0), trainable=False)
    # 将label reshape成一维
    labels = tf.reshape(labels, [-1])
 
    # 获取当前batch每个样本对应的中心
    centers_batch = tf.gather(centers, labels)
    # 计算center loss的数值
    loss = tf.nn.l2_loss(features - centers_batch)
 
    # 以下为更新中心的步骤
    diff = centers_batch - features
 
    # 获取一个batch中同一样本出现的次数，这里需要理解论文中的更新公式
    unique_label, unique_idx, unique_count = tf.unique_with_counts(labels)
    appear_times = tf.gather(unique_count, unique_idx)
    appear_times = tf.reshape(appear_times, [-1, 1])
 
    diff = diff / tf.cast((1 + appear_times), tf.float32)
    diff = alpha * diff
    # 更新中心
    centers = tf.scatter_sub(centers, labels, diff)
 
    return loss, centers

3、Focal loss

参考

def get_focal_loss(features,one_hot_labels,n):
    prob = tf.nn.softmax(features + 1e-5)
    cross_entropy = tf.multiply(one_hot_labels,tf.log(tf.clip_by_value(prob,1e-5,1.0)))
    weight = tf.pow(tf.subtract(1.0,prob),n)
    loss = -tf.reduce_mean(tf.multiply(weight,cross_entropy))
    return loss

Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

（1） 总述

       Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

（2）损失函数形式

       Focal loss是在交叉熵损失函数基础上进行的修改，首先回顾二分类交叉熵损失：

是经过激活函数的输出，所以在0-1之间。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。那么Focal loss是怎么改进的呢？

         首先在原有的基础上加了一个因子，其中γ>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。例如γ为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的γ次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

此外，加入平衡因子α，用来平衡正负样本本身的比例不均：

 

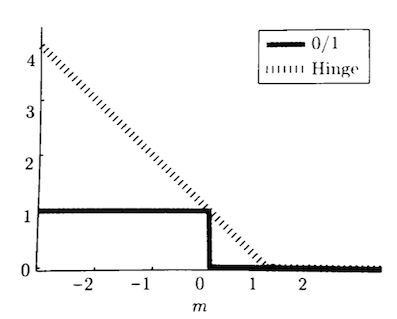
y=1的损失函数曲线对比如图所示：

      只添加α虽然可以平衡正负样本的重要性，但是无法解决简单与困难样本的问题。

     γ调节简单样本权重降低的速率，当γ为0时即为交叉熵损失函数，当γ增加时，调整因子的影响也在增加。实验发现γ为2是最优。

（3）总结

       作者认为one-stage和two-stage的表现差异主要原因是大量前景背景类别不平衡导致。作者设计了一个简单密集型网络RetinaNet来训练在保证速度的同时达到了精度最优。在双阶段算法中，在候选框阶段，通过得分和nms筛选过滤掉了大量的负样本，然后在分类回归阶段又固定了正负样本比例，或者通过OHEM在线困难挖掘使得前景和背景相对平衡。而one-stage阶段需要产生约100k的候选位置，虽然有类似的采样，但是训练仍然被大量负样本所主导。/4Triplet loss

参考

def compute_triplet_loss(anchor_feature, positive_feature, negative_feature, margin):

    """
    Compute the contrastive loss as in
    L = || f_a - f_p ||^2 - || f_a - f_n ||^2 + m
    **Parameters**
     anchor_feature:
     positive_feature:
     negative_feature:
     margin: Triplet margin
    **Returns**
     Return the loss operation
    """
	
    def compute_euclidean_distance(x, y):
        """
        Computes the euclidean distance between two tensorflow variables
        """
        d = tf.square(tf.sub(x, y))
        d = tf.sqrt(tf.reduce_sum(d)) # What about the axis ???
        return d

	
    with tf.name_scope("triplet_loss"):
        d_p_squared = tf.square(compute_euclidean_distance(anchor_feature, positive_feature))
        d_n_squared = tf.square(compute_euclidean_distance(anchor_feature, negative_feature))

        loss = tf.maximum(0., d_p_squared - d_n_squared + margin)
        #loss = d_p_squared - d_n_squared + margin

        return tf.reduce_mean(loss), tf.reduce_mean(d_p_squared), tf.reduce_mean(d_n_squared)

4、Huber loss

def huber_loss(labels, predictions, delta=1.0):
    residual = tf.abs(predictions - labels)
    condition = tf.less(residual, delta)
    small_res = 0.5 * tf.square(residual)
    large_res = delta * residual - 0.5 * tf.square(delta)
    return tf.where(condition, small_res, large_res)

    （1）定义

 

      

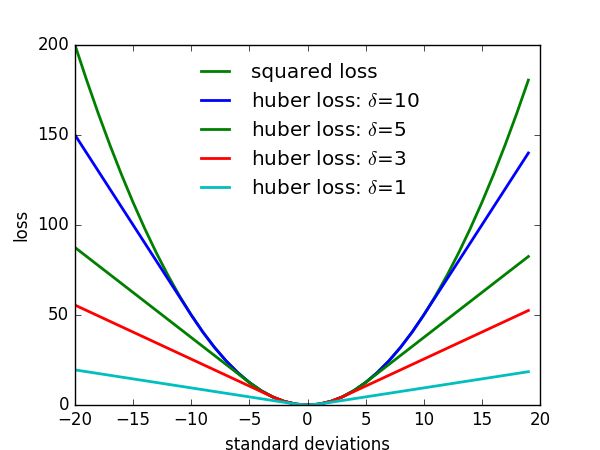
       （2）曲线

 

5、 SVM损失

包括：Hinge loss（二分类） Multiclass SVM Loss（多分类）

（1）Hinge loss

            注意：正样本标签为：，负样本标签为：

             Hinge Loss 是机器学习领域中的一种损失函数，可用于“最大间隔(max-margin)”分类，其最著名的应用是作为SVM的目标函数。 

           以为例。当时，loss为0，否则loss线性增大，函数图像如下所示： 

（2） Multiclass SVM Loss

参考

 

    附录：CS231n笔记

 

       对于当前的一组分数，对应于不同的类别，我们希望属于真实类别的那个分数比其他的类别的分数要高，并且最好要高出一个margin，这样才是安全的。反映在这个函数中，就是0的那一项的取值范围，Syi表示的是xi样本的真实类别所得到的分数，而Sj指的是其他的类别的分数，如果真实类别的分数是最大的，且大一个margin 1，那么就表示满意，也就是说不惩罚，这一项的loss为0。如果不满足这一条件，我们用下面的一段，也就是Sj - Syi + 1, 1在这里是一个常数，可以使得函数连续起来，这个Sj - Syi表示，Syi，也就是真实样本的分数比别的少的越多，我们越不满意，具体计算方式有下面这个例子：

  计算损失函数步骤：

  （1） 我们先来根据上面的流程计算“cat”类的损失值Li为：

损失函数的输出值大于零，意味着我们的预测结果不正确。

  （2）同样的，我们对第二张图像采取相同的做法，这张图片包含了一辆车：

请注意“car”的损失值为啥等于零 —— 意思是正确地预测了car的类别。

（3）最后，计算”frog”这一类的损失值：

损失函数的输出值大于零，且比较大，说明我们对frog的预测结果不正确。

（4）因此，整体损失值是：