复杂网络在信用风险中的实践

1. 传统方法

在信贷领域主要有两种风险：

欺诈风险： 借款人的目的就是骗贷。

信用风险： 又称违约风险，是借款人因各种原因，不愿或无力履行合同条件而构成违约，致使平台遭受损失。

---

​ 针对信用风险，需要对借款人的财务状况、还款意愿、履约能力等各方面因素综合量化评估，并根据风险等级制定不同的差异化定价（不同额度利率）和策略。

白话一点的解释就是：

业务： 需要训练一个模型，去预测借款人违约概率，并根据违约概率高低表示信用好坏，信用好的给予更高的额度和更低的贷款利率，针对信用较差的制定更严格的审核，更高的利率。

模型： 传统是使用评分卡，可解释性比较好。但现在越来越多会使用机器学习（如XGBoost），快速出结果且效果更好。

特征： 上图针对各个维度设计，并保证可解释性。

样本： 历史上是否违约的人群作为训练样本（都是钱啊）。

2. 复杂网络

如何将借款人所处的系统抽象成复杂网络？下面介绍基础层次和业务层次的抽象，最终得到什么样的复杂网络，以及为什么要这样做。

2.1 基础层次抽象

从原始数据中提取节点及关系抽象成复杂网络：

节点：用户、商户、公司、设备、LBS、IP/WIFI

关系：社交、消费、就职、使用、位置、上网

2.2 业务层次抽象

物以类聚，人以群分，一个人周围邻居的信用资质可以反应其自身信用资质。

基于上述业务假设对网络进一步抽象：

节点：用户

关系：社交、同位置、同设备、同公司、同商户、同WIFI…

我们为每个节点附上信用资质，最终可以得到一个复杂网络。

为什么要这么做？

1. 基础层次的抽象可以供多个不同的业务使用。

2. 基于业务经验对数据进一步精炼 garbage in garbage out。

3. 适用同类型节点的算法较多，计算复杂度低。

4. 压缩图，减少降低噪声以及缓解数据稀疏性。

目标

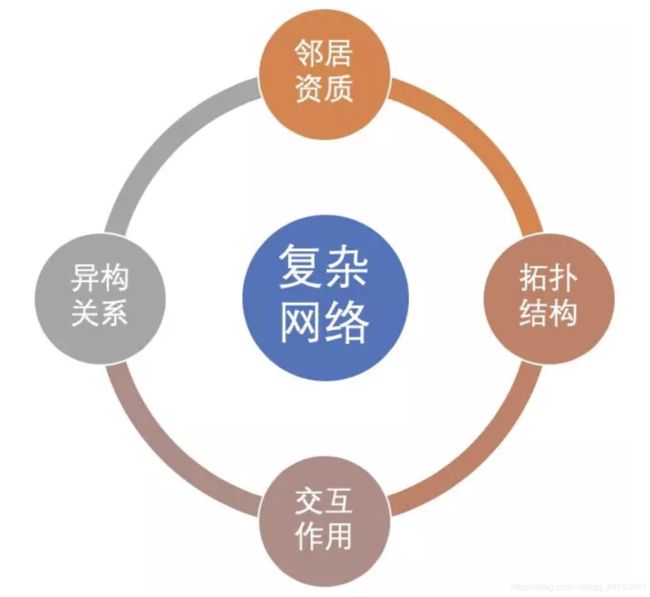
我们可以从复杂网络中抽取什么信息呢？

邻居属性： 邻居信用资质。

异构关系： 不同关系的邻居的信息。

拓扑结构： 周围邻居的拓扑结构信息

实体交互： 节点资质和邻居资质是如何交互的？

2.3 挖掘

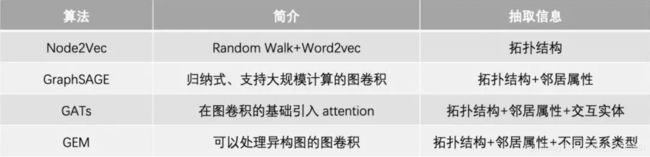
如何提取以上的信息？

上面的模型都可以是解决方案，但是也存在着一定的局限：

1. 首先GNN是黑箱，解释性不够，对于和钱直接相关的业务，对解释性的要求非常高。

2. 稳定性：金融模型上线会运行很久，对稳定性要求较高。

3. 性价比，虽然对图经过了压缩，但是也有亿级别规模，落地成本比较大，包括训练架构、算法优化等等。

如何解决这些局限性呢？

拆解上面算法，提取关键模块，用数理统计方法解题：

1. 聚合直接相连邻居特征：参考单层卷积的aggregator操作，其实也就是对邻居特征不带参数求mean、max、加权平均；
2. 获得k跳邻居特征及拓扑：可以尝试多层递归卷积 / 社区发现；
3. 与邻居特征做交互：拼接、比较、平均；
4. 如何融合异构关系：每种关系网络都通过上述方法衍生特征，不同业务通过模型来学习权重。

2.4 工程落地

某场景：借款人提交完认证资料后，触发信用评估并返回额度和利率，对时效性要求较高。

离线+实时 实现t跳邻居特征计算

离线：T+1计算好所有节点(t-1跳)特征，存储在HBASE上。

实时：借款人提交完资料后，实时查找其一跳邻居(如mysql)，调用HBASE查找每一个邻居特征，并聚合和交互生成特征。(一跳计算实时可以满足，如果谁说二跳计算实时也可以支持那就牛逼了)。

复杂网络在风控中更多是“找黑的”，比如反欺诈规则关联 N 个黑名单，N 个中介，以及团伙挖掘等。

本文是从“找白的”角度下介绍复杂网络在信用资质上的应用，方法具有普适性，在找黑的上验证效果也不错：）。

如果精力/资源有限，建议优先选择某类关系和某些节点特征进行实验：

关系选择： 优选覆盖度较高、噪声低、符合业务直觉的关系，如社交、支付，像LBS虽然覆盖度高，但是噪声也是比较大，在使用时需要谨慎。

节点特征选择：优先选择已被验证效果不错的特征，如收入、信用额度等。

另外值得注意的是，比较容易数据穿越，有多个时间需要考虑，如”申请时间“、“建立关系时间”、“特征时间”等。

2.5 具体实践

2.5.1 聚合一跳邻居特征

一跳邻居即直接相连的邻居，我们需要设计一个聚合函数，在考虑关系权重的基础上，如何表示一跳邻居特征分布。

如下图所示，假设是关系为亲密度、节点特征为收入，如何聚合借款人不同亲密度的邻居收入特征？
我们可以设计这样的聚合函数来加工信息（不考虑未知）：

简单平均：
$$\frac{5k+20k+30k}{3}=18.3k$$
假设不同亲密度的朋友对借款人信用风险的影响是相同的（假设收入一样）。

加权平均：
$$\frac{0.1\times 5k+0.2\times 20k+0.2\times 30k}{0.1+0.2+0.3}=21k$$
假设亲密好友收入高低对借款人信用风险影响较大。

最大值：
$$\max \{5k,20k,30k\}=30k$$
假设亲密好友收入高低对借款人信用风险影响较大。

哪个聚合函数效果比较好？不同聚合函数的业务假设是不同的，建议都使用。特征工程即把可能有用的特征都加工出来，再通过 y 做特征选择。

特征取值“未知”，怎么处理？因为未知其实也可能包含信息，建议聚合计算分考虑未知和不考虑未知进行计算。

邻居特征是离散的，怎么聚合？转换成one-hot编码，计算在属于某个类别邻居比例。

2.5.2 聚合多跳邻居特征

问题：邻居数量随着“跳数”增加而指数增长，直接获得借款人多跳邻居比较困难。假设平均节点度为100，那么每个借款人一跳邻居数量为100，二跳邻居100^{2，三跳邻居100}3。

下面介绍“多跳递归传播”和”社区发现“这两种方法

2.5.2.1 多跳递归传播

以计算二跳邻居特征为例，该方法大概的思路是：将当前节点的二跳邻居特征传播到一跳邻居上，然后将一跳邻居新特征再传播到当前节点。

细节：

1. 因为每次传播只会涉及直接相连的邻居，故计算复杂度大为降低。

2. 原文前向传播计算是带参数W的，这里简化为将所有参数相等（因为是特征工程，不是学习，故会损失一些信息）

3. 对邻居节点进行固定数量抽样，而不是取全部（避免数据倾斜），采样方法使用计算复杂度为O(1)的Alias Method。

4. 递归实现，每轮对所有节点聚合其邻居（隐）特征及交互，并更新节点特征，作为下一轮输入。

5. 第一轮得到所有节点一跳邻居特征，第二轮得到二跳邻居特征，以此类推。

2.5.2.2 社区发现

大致思路：通过社区发现算法将graph分成一个个社区，然后计算每个节点所属社区的特征，如社区中黑名单比例、社区中平均收入。

这种方法相当于对多跳邻居根据拓扑结构进行了分类（社区），故额外提取了网络中拓扑结构信息。

工业界graph规模比较大，一般会用Louvain，速度快，效果也不错，下面是spark版本实现：

https://link.zhihu.com/?target=https%3A//github.com/Sotera/spark-distributed-louvain-modularity

2.5.3 实体间特征交互

聚合邻居特征h1后，如何与自身特征h2做交互？

拼接：直接将h1拼接作为其一个新的特征

比较：h1-h2 或者 h1/h2 。例如求邻居平均收入与借款人自身收入差距较大，是否有异常？

平均：(h1+h2)/2。

最大值：max(h1,h2)，金融是重召回的，若特征表示风险程度，这样即取最大风险。

2.5.4 处理不同异构关系

将异构关系拆成多个单一关系，每个关系都经过上述方法生成特征，供下游不同场景使用。

这样做的好处是：不同关系权重在不同场景是不同的，应该是通过这些场景的y去学习。

形式化描述：

有$|D|$种类型关系，则可以拆解为$|D|$个graph: $\{g^{\{d\}}=(V,E^{(d)},d\in |D|)\}$

将上面提取graph特征方法记为 $f$

对每个$g^{\{d\}}$，都可以通过方法$f$ 提取特征$X^{\{d\}}=f(g^{\{d\}})$

将不同的$X^{\{d\}}$作为下游任务的输入特征，根据任务目标来赋予权重。

借鉴蚂蚁处理异构网络的思路：

https://zhuanlan.zhihu.com/p/59666737

3. 附录

3.1 不同社区发现算法比较

在实际小规模graph上对比了主流的社区发现算法，Louvain在划分社区质量和划分稳定性上均表现不错的，且能分布式实现。

3.1.1 社区发现算法

• Walktrap：基于随机游走的社区发现算法 《Computing communities in large networks using random walks》

• Leading Eigenvector：基于特征矩阵求模块度，自底而上定层次聚类《Finding community structure in networks using the eigenvectors of matrices》

• Fast-Greedy：自底而上的层次聚类《Finding community structure in very large networks》

• Louvain：基于模块度最大化的算法《Fast unfolding of communities in large networks》

• LPA：基于标签传播多社区发现算法 《Near linear time algorithm to detect community structures in large-scale networks.》

3.1.2 实验graph

下面是脱敏后的实验网络的规模：

3.1.3 划分质量：模块度指标

3.1.4 划分数量合理性

3.1.5 可视化

这是louvain划分的某个graph的可视化效果（绘制工具：gephi）

感谢
参考原文：https://zhuanlan.zhihu.com/p/90813791