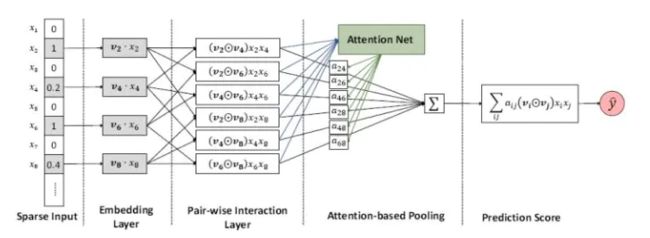
1.AFM模型pytorch实现。
$\hat{y}_{AFM}=w_{0} + \sum_{i=1}^{n}w_{i}x_{i}+p^{T}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}a_{ij}(v_{i}v_{j})x_{i}x_{j}$
$a_{ij}^{'}=h^{T}Relu(W(v_{i}v_{j})x_{i}x_{j}+b)$
$a_{ij}=\frac{exp(a_{ij}^{'})}{\sum_{i,j}exp(a_{ij}^{'})}$
(实际数据使用的是Dataloader,需要设置batch_size等参数。)
设原来的数据有num_fields =3个特征,one-hot编码过后对应有30维度,嵌入维度设为ebd_size=4。所以嵌入层定义为
ebd_size = 4
ebd = nn.Embedding(30,ebd_size)
自定义一个batch_size的数据
x_ = [[1, 13, 22], [0, 18,29],[2, 13,27], [0, 11,22],[1, 14,26]] #shape=batch_size*num_fields
x_ = Variable(torch.LongTensor([[1, 13, 22], [0, 18,29],[2, 13,27], [0, 11,22],[1, 14,26]]))
得到对应的嵌入向量
x=ebd(x_)
计算交叉特征:
$(v_{i}v_{j})x_{i}x_{j}$
交叉特征数目=num_fields*(num_fields - 1)/2
inner_product的shape为batch_size*交叉特征数目*嵌入维度
num_fields = x.shape[1] row, col = list(), list() for i in range(num_fields - 1): for j in range(i + 1, num_fields): row.append(i), col.append(j) p, q = x[:, row], x[:, col] inner_product = p * q
接下来求得
$Relu(W(v_{i}v_{j})x_{i}x_{j}+b)$
用一个nn.Linear层,在经过一个Relu激活函数可以完成
attention(inner_product))结果的shape为 batch_size*交叉特征*嵌入维度
attention = torch.nn.Linear(ebd_size, ebd_size) print(attention(inner_product)) # batch_size*交叉特征*嵌入维度 attn_scores = F.relu(attention(inner_product)) print("attn_scores", attn_scores) # batch_size*交叉特征*嵌入维度
接下来在经过一个linear得到$a_{ij}^{'}$
$a_{ij}^{'}=h^{T}Relu(W(v_{i}v_{j})x_{i}x_{j}+b)$
projection = torch.nn.Linear(ebd_size, 1) print("projection(attn_scores)", projection(attn_scores)) # batch_size*交叉特征*1
在经过一个softmax得到
$a_{ij}=\frac{exp(a_{ij}^{'})}{\sum_{i,j}exp(a_{ij}^{'})}$
attn_scores = F.softmax(projection(attn_scores), dim=1) print("attn_scores", attn_scores) # batch_size*交叉特征*1
接下来把交叉特征$(v_{i}v_{j})x_{i}x_{j}$与注意力权重$a_{ij}$相乘
print("attn_scores * inner_product", attn_scores * inner_product) # batch_size*交叉特征*嵌入维度 attn_output = torch.sum(attn_scores * inner_product, dim=1) print("attn_output", attn_output) # batch_size*嵌入维度
最后经过一个输出大小为1的全连接层
fc = torch.nn.Linear(ebd_size, 1) fc_out = fc(attn_output) print("fc_out", fc_out) # batch_size*1
这样就把$p^{T}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}a_{ij}(v_{i}v_{j})x_{i}x_{j}$求出来了,前面一阶部分使用一个Linear层就可以求得到
参考代码:
import torch import numpy as np from torch.autograd import Variable import torch.nn.functional as F import torch.nn as nn ebd_size = 4 ebd = nn.Embedding(30,ebd_size) x_ = Variable(torch.LongTensor([[1, 13, 22], [0, 18,29],[2, 13,27], [0, 11,22],[1, 14,26]])) x=ebd(x_) num_fields = x.shape[1] row, col = list(), list() for i in range(num_fields - 1): for j in range(i + 1, num_fields): row.append(i), col.append(j) p, q = x[:, row], x[:, col] inner_product = p * q print("inner_product", inner_product) # batch_size*交叉特征*嵌入维度 attention = torch.nn.Linear(ebd_size, ebd_size) print(attention(inner_product)) # batch_size*交叉特征*嵌入维度 attn_scores = F.relu(attention(inner_product)) print("attn_scores", attn_scores) # batch_size*交叉特征*嵌入维度 projection = torch.nn.Linear(ebd_size, 1) print("projection(attn_scores)", projection(attn_scores)) # batch_size*交叉特征*1 attn_scores = F.softmax(projection(attn_scores), dim=1) print("attn_scores", attn_scores) # batch_size*交叉特征*1 print("attn_scores * inner_product", attn_scores * inner_product) # batch_size*交叉特征*嵌入维度 attn_output = torch.sum(attn_scores * inner_product, dim=1) print("attn_output", attn_output) # batch_size*嵌入维度 fc = torch.nn.Linear(ebd_size, 1) fc_out = fc(attn_output) print("fc_out", fc_out) # batch_size*1 exit()