深度学习笔记（3） 向量化逻辑回归

---

1. 向量化运算的优势

python的向量化运算速度快，是非常基础的去除代码中for循环的艺术

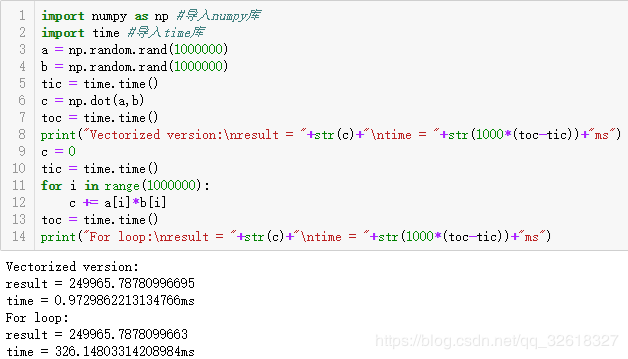
可以看出相同的运算，时间相差接近335倍

---

2. 向量化编程

训练输入一个 (n_x × m)的矩阵 X
首先计算Z：[z⁽¹⁾ z⁽²⁾…z^(m) )]=[w^T x⁽¹⁾, w^T x⁽²⁾…w^T x^(m)] + [b b…b]
[b b…b] 是一个 1×m矩阵或者是一个 m 维的行向量
W^T X是一个 m 维的行向量
w 转置乘以 x⁽¹⁾ ， x⁽²⁾ 一直到 x^(m)
所以 w 转置是一个1×n行向量，w是一个 n 维的列向量

最终得到了另一个 1×m 的向量：
[z⁽¹⁾ z⁽²⁾… z^(m)] = w^T X + [b b…b] = [w^T x⁽¹⁾+b,w^T x⁽²⁾+b … w^T x^(m)+b]

Numpy 表示Z：Z = np.dot(w.T, X) + b
Python广播（broadcasting）功能自动把实数 b 扩展成 1×m 的行向量

A = [a⁽¹⁾ a⁽²⁾…a^(m)] = $\sigma$(Z)，一次性计算所有 a
即同一时间内完成m个训练样本的前向传播向量化计算

目标是一次迭代实现一次梯度下降并且不使用for循环，而是向量，可以这么做：

过程中可以用维持 assert(Z.shape == (1,m)) 或者重组 Z. reshape(1,m) 来确保的矩阵或向量所需要的维数

---

3. 举例

输入x是3个数值(a,b,c)，如果a+c>b，则输出 y = 1，否则 y = 0
利用逻辑回归中的梯度下降，构建一个简单的神经网络
此处使用标准化和正则化，有助于优化机器学习，在后续文章再作详细介绍

首先，定义激活函数：

import numpy as np
import matplotlib.pyplot as plt


def sigmoid(z):  # 激活函数
    a = 1 / (1 + np.exp(-z))
    return a

接下来，定义激活函数的导数：

def d_sigmoid(a):  # 激活函数的导数
    return a * (1 - a)

导入数据：

X = np.array(
    [[0.1, 1.1, 0.5], [1.1, 0.1, 1.5], [0.3, 1.4, 0.7], [1.4, 0.1, 1.1], [0.5, 1.8, 0.9], [1.0, 0.6, 1.8],
     [0.7, 1.9, 0.1], [1.1, 0.2, 1.3], [0.9, 2.1, 0.8], [1.5, 0.1, 1.8], [0.1, 1.8, 0.6], [1.5, 0.3, 1.9],
     [0.3, 1.7, 0.2], [1.7, 0.4, 1.5], [0.5, 1.1, 0.3], [1.6, 0.6, 1.8], [0.7, 1.5, 0.2], [1.5, 0.8, 1.2],
     [0.9, 1.9, 0.5], [1.9, 1, 2.6]])
X = X.T  # 转置X

y = np.array(
    [[0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1]])

m = X.shape[1]
X = (X - np.mean(X)) / np.linalg.norm(X, ord=2, axis=1, keepdims=True)  # 标准化输入

初始化权重和超参数

w1 = np.random.randn(3, 4) * np.sqrt(1 / 3)  # 权重初始化
b1 = np.random.randn(4, 1)
w2 = np.random.randn(4, 1) * np.sqrt(1 / 4)
b2 = np.random.randn(1, 1)
alpha = 1  # 学习效率
lambd = 0.03  # 正则化参数
cost = np.zeros(500)  # 初始化记录代价的列表

迭代：

for i in range(0, 500):  # 迭代500次
    # 向前传播
    Z1 = np.dot(w1.T, X) + b1
    A1 = sigmoid(Z1)
    Z2 = np.dot(w2.T, A1) + b2
    A2 = sigmoid(Z2)
    # 反向传播
    dz2 = (A2 - y)
    dw2 = np.dot(A1, dz2.T) / m + lambd * w2 / m
    db2 = np.sum(dz2, axis=1, keepdims=True) / m
    dz1 = np.dot(w2, dz2) * d_sigmoid(A1)
    dw1 = np.dot(X, dz1.T) / m + lambd * w1 / m
    db1 = np.sum(dz1, axis=1, keepdims=True) / m
    # 更新权重
    w2 = w2 - alpha * dw2
    b2 = b2 - alpha * db2
    w1 = w1 - alpha * dw1
    b1 = b1 - alpha * db1
    # 记录代价（损失、误差）
    cost[i] = -1 / m * np.sum(y * np.log(A2) + (1 - y) * np.log(1 - A2))

运行上面的一个简单的神经网络，得到在学习过程中的代价记录图：

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置正常显示中文
plt.plot(cost, "b", label='代价')  # 设置曲线数值
plt.xlabel("迭代次数")  # 设置X轴的名字
plt.ylabel("代价")  # 设置Y轴的名字
plt.title("代价变化图")  # 设置标题
plt.legend()  # 设置图例
plt.show()  # 显示图表

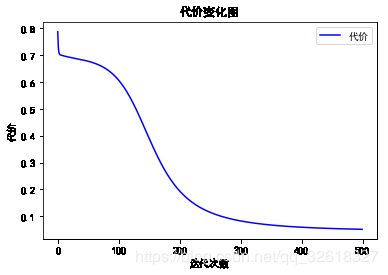
可以看出，代价在迭代500次后已经逐渐接近于0，说明预测的准确度很接近100%

显示所求的权重w和b

print("w1:" + str(w1) + "\nw2:" + str(w1))  # 显示权重
print("b1:" + str(b1) + "\nb2:" + str(b2))

w1:[[ 3.53485299  2.41501319 -1.69594659 -0.46506595]
    [-3.95670511 -2.90826621  2.73447831  1.24344382]
    [ 3.1645732   2.29206756 -2.2545134  -0.80372522]]
w2:[[ 3.53485299  2.41501319 -1.69594659 -0.46506595]
    [-3.95670511 -2.90826621  2.73447831  1.24344382]
    [ 3.1645732   2.29206756 -2.2545134  -0.80372522]]
b1:[[ 0.01965446]
    [-0.02949129]
    [ 0.05821271]
    [-1.00424847]]
b2:[[-2.5647781]]

再利用求出的w和b进行预测验证：

def predict(x):  # 预测函数
    x = np.array([x])
    x = (x.T - np.mean(x)) / np.linalg.norm(x, ord=2, axis=1, keepdims=True)
    z1_test = np.dot(w1.T, x) + b1
    a1_test = sigmoid(z1_test)
    z2_test = np.dot(w2.T, a1_test) + b2
    a2_test = sigmoid(z2_test)
    return a2_test


print("predict 0 rate:%f%%" % ((1 - predict([0.1, 0.7, 0.5])) * 100))
print("predict 0 rate:%f%%" % ((1 - predict([0.9, 1.8, 0.5])) * 100))
print("predict 1 rate:%f%%" % (predict([1.2, 1.0, 1.5]) * 100))
print("predict 1 rate:%f%%" % (predict([1.8, 0.1, 1.9]) * 100))

predict 0 rate:99.518280%
predict 0 rate:99.713837%
predict 1 rate:92.412660%
predict 1 rate:99.882484%

可以看出，预测的准确率还是挺高的。

[1] python的代码地址:
https://github.com/JoveH-H/A-simple-explanation/blob/master/easyBPNN.py
[2] jupyter notebook的代码地址:
https://github.com/JoveH-H/A-simple-explanation/blob/master/ipynb/easyBPNN.ipynb

---

参考：

《神经网络和深度学习》视频课程

---

相关推荐：

深度学习笔记（2） 神经网络基础
深度学习笔记（1） 深度学习简介

---

谢谢！