最短路径之迪杰斯特拉(Dijkstra)算法

定义

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

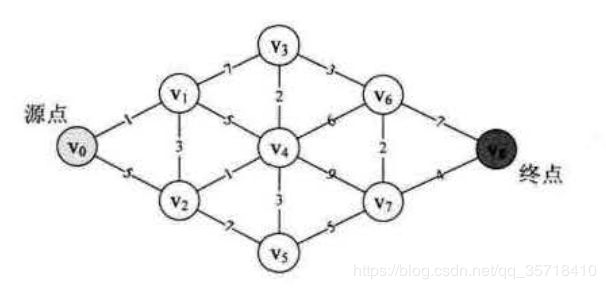
如图所示，我们要求解V0到V8的最小权值及最短路径，这是我们经常碰到的求最小路径问题之一。通过一步就将最短权值和路径求出是不现实的，不过我们可以通过迪杰斯特拉算法，将所有点及个点之间的权值转换为矩阵，也就是二维数组，然后逐步求出最短路径即可。
二维矩阵数组如下图：

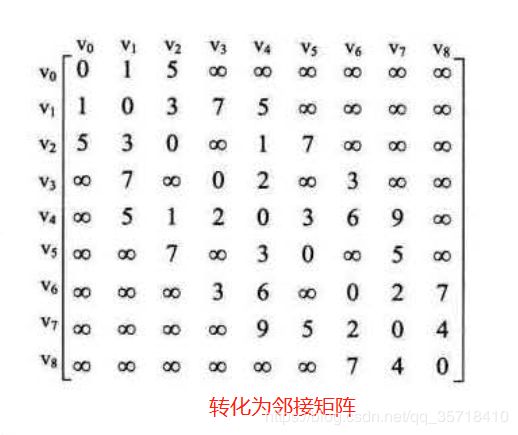
TS代码如下：

class Dikastra{
  private arc:Array<any> = [];
  private numVertexes = 0; //顶点数
  private vexs:Array<string> = []; //顶点表
  private pathmatirx:Array<number> = []; // 用于存储最短路径下标的数组，下标为各个顶点，值为下标顶点的前驱顶点
  private shortPathTable:Array<number> = []; //用于存储到各点最短路径的权值和
  private final:Array<any> = []; //用于标记V0到V8每个点是否找到了最短路径

  /**
   * 生成V0 到 V8 顶点
   */
  private createVertexs(){
    for(let i=0;i<this.numVertexes;i++){
      this.vexs.push('V' + i);
    }
  }

  /**
   * 初始化状态标记及最短路径表
   */
  private initTables(){
    this.final.length = this.pathmatirx.length = this.shortPathTable.length = 0;
    for (let v = 0; v < this.numVertexes; v++) {
      this.final[v] = v === 0 ? 1 : 0; //V0默认是已找到最短路径状态
      this.shortPathTable[v] = v === 0 ? 0 : this.arc[0][v]; //V0自己到自己是0
      this.pathmatirx[v] = 0;
    }
  }

  /**
   * 执行迪杰斯特拉算法
   */
  private dijkstra(){
    let k:number;    //当前找到的最近路线上的最后一个顶点，通过此顶点去找最近路线上的下一个顶点
    let min:number;  //到当前顶点的最小权值，65535意味着相距无穷大（不挨着初始时距离权值是无穷大）
    for (let v = 1; v < this.numVertexes; v++) {
      //初始化数据
      min = 65535;
      for (let w = 0; w < this.numVertexes; w++) {
        //寻找离V0最近的顶点
        if (!this.final[w] && this.shortPathTable[w] < min) {
          k = w;
          min = this.shortPathTable[w]; //w 顶点离V0顶点更近
        }
      }
      this.final[k] = 1; //将目前找到的最近的顶点置位1
      for (let w = 0; w < this.numVertexes; w++) {
        const curPathVal = min + this.arc[k][w];
        //修正当前最短路径及距离
        if (!this.final[w] && curPathVal < this.shortPathTable[w]) {
          //说明找到了更短的路径，修改Pathmatirx[w]和ShortPathTable[w]
          this.shortPathTable[w] = curPathVal;
          this.pathmatirx[w] = k;
        }
      }
    }
  }

  /**
   * 获取最短距离权值
   * @param Vn 终点
   * @returns 到终点的距离权值
   */
  public getShortPath(Vn:number){
    //打印V0-Vn最短路径
    console.log(
      "%s-%s 最小权值和: %d",
      this.vexs[0],
      this.vexs[Vn],
      this.shortPathTable[Vn]
    );
    let temp = Vn,
    str = "";
    while (temp != 0) {
      str = "->" + this.vexs[temp] + str;
      temp = this.pathmatirx[temp];
    }
    str = "V0" + str;
    console.log("最短路线：" + str);
    return this.shortPathTable[Vn];
  }

  /**
   * 设置arc矩阵，重新计算矩阵最短距离权值
   */
  public setArc(arc:Array<any>){
    this.arc = arc;
    this.numVertexes = arc[0].length;
    //生成顶点
    this.createVertexs();
    //初始化最短路径表及是否已找到最短路径关联数组
    this.initTables();
    //执行迪杰斯特拉算法寻找最短路径
    this.dijkstra();
  }
}

js版本代码如下：

var Dikastra = /** @class */ (function () {
    function Dikastra() {
        this.arc = [];
        this.numVertexes = 0; //顶点数
        this.vexs = []; //顶点表
        this.pathmatirx = []; // 用于存储最短路径下标的数组，下标为各个顶点，值为下标顶点的前驱顶点
        this.shortPathTable = []; //用于存储到各点最短路径的权值和
        this.final = []; //用于标记V0到V8每个点是否找到了最短路径
    }
    /**
     * 生成V0 到 V8 顶点
     */
    Dikastra.prototype.createVertexs = function () {
        for (var i = 0; i < this.numVertexes; i++) {
            this.vexs.push('V' + i);
        }
    };
    /**
     * 初始化状态标记及最短路径表
     */
    Dikastra.prototype.initTables = function () {
        this.final.length = this.pathmatirx.length = this.shortPathTable.length = 0;
        for (var v = 0; v < this.numVertexes; v++) {
            this.final[v] = v === 0 ? 1 : 0; //V0默认是已找到最短路径状态
            this.shortPathTable[v] = v === 0 ? 0 : this.arc[0][v]; //V0自己到自己是0
            this.pathmatirx[v] = 0;
        }
    };
    /**
     * 执行迪杰斯特拉算法
     */
    Dikastra.prototype.dijkstra = function () {
        var k; //当前找到的最近路线上的最后一个顶点，通过此顶点去找最近路线上的下一个顶点
        var min; //到当前顶点的最小权值，65535意味着相距无穷大（不挨着初始时距离权值是无穷大）
        for (var v = 1; v < this.numVertexes; v++) {
            //初始化数据
            min = 65535;
            for (var w = 0; w < this.numVertexes; w++) {
                //寻找离V0最近的顶点
                if (!this.final[w] && this.shortPathTable[w] < min) {
                    k = w;
                    min = this.shortPathTable[w]; //w 顶点离V0顶点更近
                }
            }
            this.final[k] = 1; //将目前找到的最近的顶点置位1
            for (var w = 0; w < this.numVertexes; w++) {
                var curPathVal = min + this.arc[k][w];
                //修正当前最短路径及距离
                if (!this.final[w] && curPathVal < this.shortPathTable[w]) {
                    //说明找到了更短的路径，修改Pathmatirx[w]和ShortPathTable[w]
                    this.shortPathTable[w] = curPathVal;
                    this.pathmatirx[w] = k;
                }
            }
        }
    };
    /**
     * 获取最短距离权值
     * @param Vn 终点
     * @returns 到终点的距离权值
     */
    Dikastra.prototype.getShortPath = function (Vn) {
        //打印V0-Vn最短路径
        console.log("%s-%s 最小权值和: %d", this.vexs[0], this.vexs[Vn], this.shortPathTable[Vn]);
        var temp = Vn, str = "";
        while (temp != 0) {
            str = "->" + this.vexs[temp] + str;
            temp = this.pathmatirx[temp];
        }
        str = "V0" + str;
        console.log("最短路线：" + str);
        return this.shortPathTable[Vn];
    };
    /**
     * 设置arc矩阵，重新计算矩阵最短距离权值
     */
    Dikastra.prototype.setArc = function (arc) {
        this.arc = arc;
        this.numVertexes = arc[0].length;
        //生成顶点
        this.createVertexs();
        //初始化最短路径表及是否已找到最短路径关联数组
        this.initTables();
        //执行迪杰斯特拉算法寻找最短路径
        this.dijkstra();
    };
    return Dikastra;
}());

引入js，然后console打印出测试结果：

<!DOCTYPE html>
<html lang="en">
  <head>
    <meta charset="UTF-8" />
    <meta name="viewport" content="width=device-width, initial-scale=1.0" />
    <meta http-equiv="X-UA-Compatible" content="ie=edge" />
    <title>Document</title>
  </head>
  <body></body>
  <script src="./dikastra.js"></script>
  <script>
    const dikastra = new Dikastra();
    //定义图的二维矩阵
    const arc1 = [
      [0, 1, 5, 65535, 65535, 65535, 65535, 65535, 65535],
      [1, 0, 3, 7, 5, 65535, 65535, 65535, 65535],
      [5, 3, 0, 65535, 1, 7, 65535, 65535, 65535],
      [65535, 7, 65535, 0, 2, 65535, 3, 65535, 65535],
      [65535, 5, 1, 2, 0, 3, 6, 9, 65535],
      [65535, 65535, 7, 65535, 3, 0, 65535, 5, 65535],
      [65535, 65535, 65535, 3, 6, 65535, 0, 2, 7],
      [65535, 65535, 65535, 65535, 9, 5, 2, 0, 4],
      [65535, 65535, 65535, 65535, 65535, 65535, 7, 4, 0]
    ];
    
    dikastra.setArc(arc1);
    console.log(dikastra.getShortPath(8));

    //如果想获取V5到V8的最短权值路径，重新构建V5到V8的矩阵即可
    const arc2 = [
      [0,65535,5,65535],
      [65535,0,2,7],
      [5,2,0,4],
      [65535,7,4,0]
    ];
    dikastra.setArc(arc2);
    console.log(dikastra.getShortPath(3));
  </script>
</html>

打印结果如下：

如果想要获取V5到V8的最短路径，只需要构建V5到V8的二维矩阵，然后重新setArc，调用getShortPath方法获取结果即可。