台大李宏毅教授机器学习HW2 作业二 赢家还是输家
首先数据文件https://pan.baidu.com/s/1BPCNWVSFUG_zryJuk4CiXA
好像在网上只能搜到这一个文件,是一个4000*58的表格,其中最后一列表示标签,如果是0的话表示工资小于50k,如果是1表工资大于50k,前57列是一个人的不同属性,我们需要用这57个属性来预测一个人的工资是否会大于50k
由于只有一个文件,所以将文件的80%用作训练,其余部分用作测试。
import numpy as np
import pandas as pd
def read2train():
path = 'F:\\python_book\\machine_learning\\spam_train.csv'
t = pd.read_csv(path)
t = t.iloc[:, 1:]
data = np.array(t, float)
index = int(data.shape[0]*0.8)
train_x = data[:index, :-1]
train_y = data[:index, -1]
# 由于文件中的标签只有一列,但是这是一个二分类问题,所以我在这里进行了处理
# 已知1表示大于50k 0表示小于50k,那么1-train_y的值若是1就表示小于50k的概率为1
# 若是0就表示小于50k的概率为0,这样做是为了与sigmoid的结果求误差
a = 1 - train_y
train_y = np.vstack((train_y, a)).reshape(train_x.shape[0], -1)
test_x = data[index:, :-1]
test_y = data[index:, -1].reshape(test_x.shape[0], -1)
a = 1 - test_y
test_y = np.vstack((test_y, a)).reshape(test_x.shape[0], -1)
return train_x, train_y, test_x, test_y
import numpy as np
def softmax(x):
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
'''
由于one-hot表示中t为0的元素的交叉熵也为0,因此针对这些元素的计算可以忽略。
只需要获得网络中在正确解标签处的输出即可计算交叉熵误差,1e-7 是为了防止出现负无穷大的结果
'''
def cross_entry_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = int(y.shape[0])
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# 动量法更新参数
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key]**2
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 乘法层的实现,用来进行w*x+b的前向和后向传播
class Affine:
def __init__(self, w, b):
self.w = w
self.b = b
self.x = None
self.dw = None
self.db = None
def forward(self, x):
self.x = x
return np.dot(x, self.w) + self.b
def backward(self, dout):
self.dw = np.dot(self.x.T, dout)
dx = np.dot(dout, self.w.T)
self.db = np.sum(dout, axis=0)
return dx
# Sigmoid用来实现Sigmoid函数的前向和后向传播
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
self.out = 1 / (1 + np.exp(-x))
return self.out
def backward(self, dout):
dx = dout * (1 - self.out) * self.out
return dx
# 对进过进行softmax计算出概率之后,求出交叉熵误差,这层反向传播的结果是y-t
# 最后面除以batch_size,则传给前面层的是单个数据的误差
# 我试了一下不写这句,好像收敛的幅度更大,但这种写法是我在参考书上看的,所以就照做了
class SoftMaxWithLoss:
def __init__(self):
self.loss = None # 交叉熵误差
self.y = None # softmax的输出
self.t = None # 监督数据
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entry_error(self.y, self.t)
return self.loss
def backward(self):
batch_size = self.y.shape[0]
dx = (self.y - self.t) / batch_size
return dx
from util import *
from collections import OrderedDict
class Net:
def __init__(self, input_size, output_size):
self.params = {}
self.params['w1'] = np.random.randn(input_size, output_size)
self.params['b1'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['w1'], self.params['b1'])
self.layers['Sigmoid1'] = Sigmoid()
self.lastLayer = SoftMaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def gradient(self, x, t):
loss = self.loss(x, t)
dout = self.lastLayer.backward()
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['w1'] = self.layers['Affine1'].dw
grads['b1'] = self.layers['Affine1'].db
return grads
def accuracy(self, x, t):
y = self.predict(x)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
from read_Data import *
from logistic_regression import *
train_x, train_y, test_x, test_y = read2train()
network = Net(train_x.shape[1], 2)
Ada = AdaGrad(lr=0.001)
Mom = Momentum()
for i in range(100000):
grads = network.gradient(train_x, train_y)
# Mom.update(network.params, grads)
Ada.update(network.params, grads)
if i % 1000 == 0:
acc = network.accuracy(test_x, test_y)
print(i, acc)
最后准确率能达到90以上
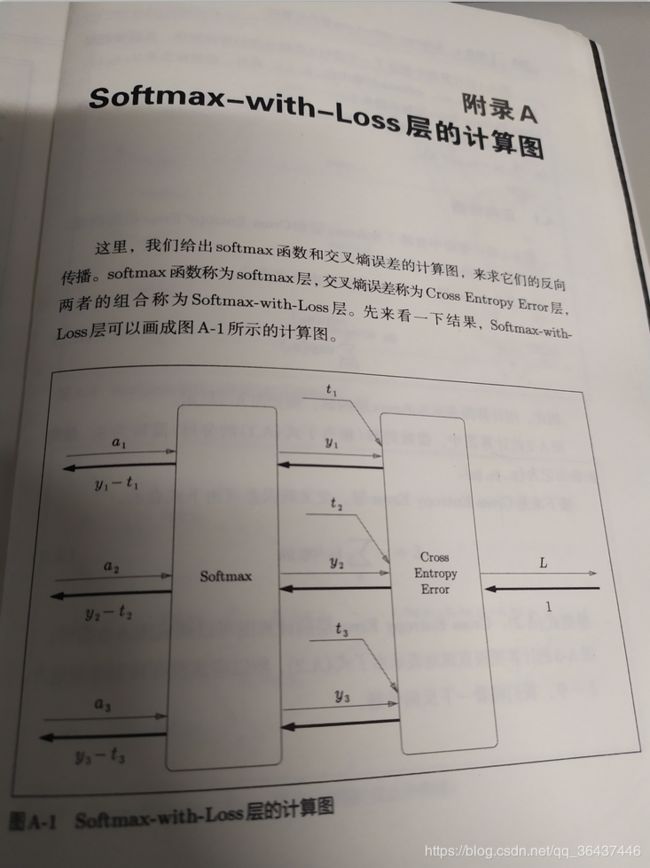
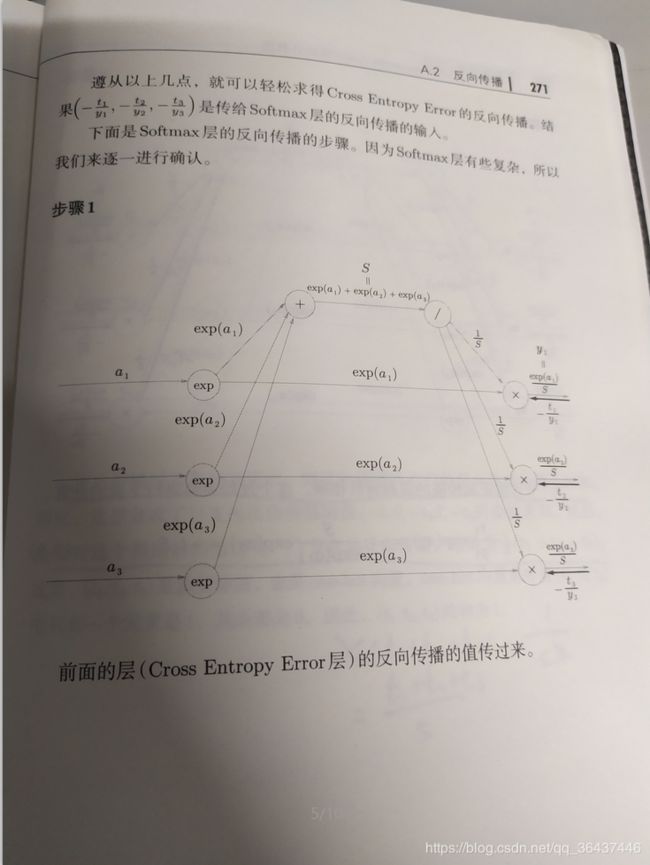
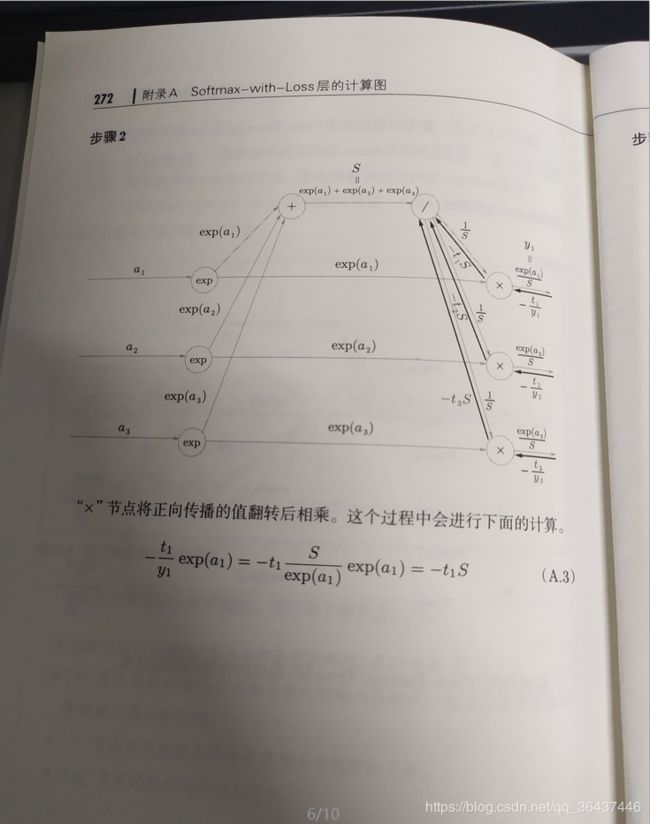
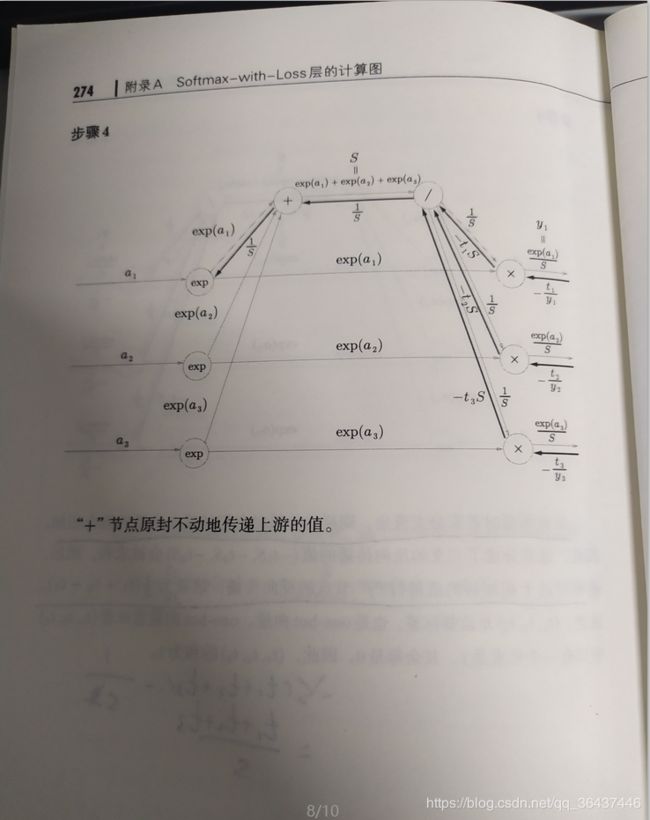
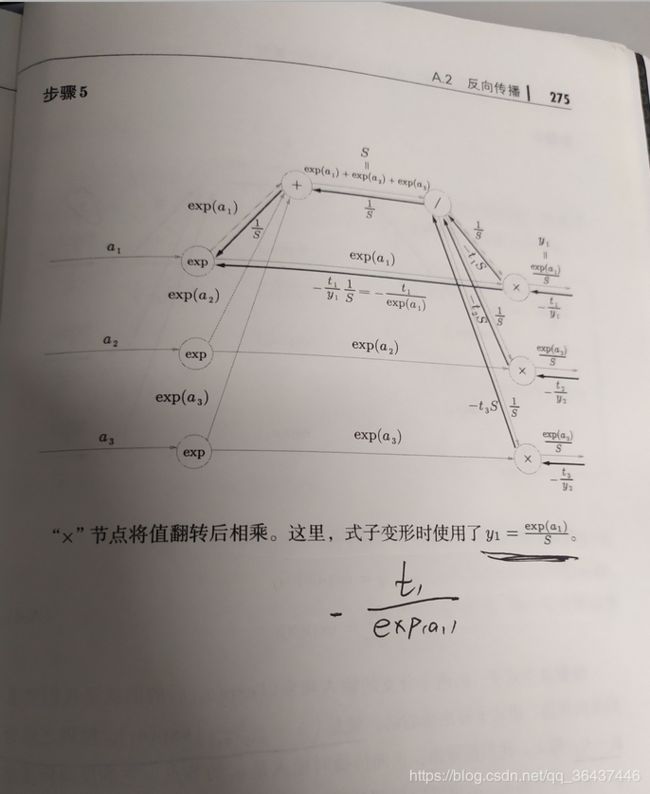
下面这些图片来帮助大家理解相关公式的来由
补充:由于本人是新手,且网上关于李宏毅教授的作业二的资料较少,我就写了一个发出来,不管是代码的深度还是规范程度上来讲都得往后稍一稍,但我还是希望能帮助到在入门的各位同行们!冲就完事儿了
欢迎大家在下面评论讨论共同进步!