doolittle分解法解线性方程

doolittle分解法解线性方程

相比于gauss分解法解线性方程组，doolittle分解法虽然复杂点，但是对于高阶线性方程，处理起来更明了，简洁，目的性更强。A =(a(i,j)),n×n矩阵，进行doolittle分解为单位下三角矩阵L = (l(i,j)),上三角矩阵U = (u(i,j));矩阵A中第r列主对角元右边(含主对角元)的对应元素，得a(r,i) = l(r,k)×u(k,i)的求和(kc从1到r，r从1到n )，再对比等式两边主对角元以下(不含主对角元)的对应元素，得：a(i,r) = l(i,k)×u(k,r)的求和,(i从r+1到n，r从1到n-1)；由此我们可以得到公式如图一：

题目：A = {{ 5,7,9,10}，{6,8,10,9}，{7,10,8,9}，{5,7,6,5}}，b = {26,18,22,9};Ax = b;求线性方程的解x;

图一

doolittle分解又称为LU分解，即把矩阵A分解成两个同阶的单位下三角矩阵L和上三角矩阵U，Ly = b,Ux = y;

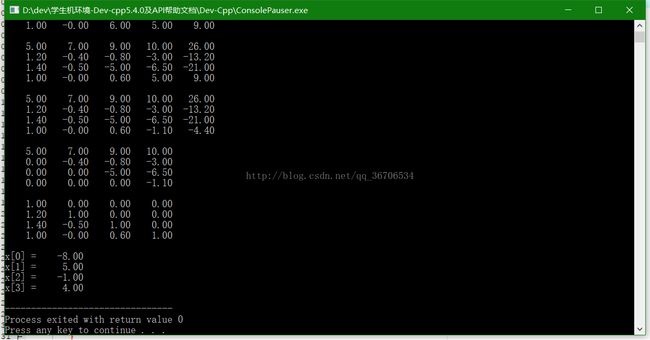
结果：x[4] = {-8,5,-1,4}

#include
#define N 4

int main(){
	int Doolittle(double *a,double b[],double *c,double *d,double x[]);
	double a[N][N] = {{5,7,9,10},{6,8,10,9},{7,10,8,9},{5,7,6,5}};
	double b[N] = {26,18,22,9};
	double c[N][N] = {0};
	double d[N][N] = {{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}};
	double x[N];
	int i;
	if(Doolittle(&a[0][0],b,&c[0][0],&d[0][0],x) != 0){
		for( i = 0;iN)break;//需要注意的是当r=2,i=3时，此时会发生覆盖，所以必须要这个条件 
	 				count = count + 1;
	 				temp = temp + a[(count-1)*N + i + r - 1]*a[r*N + count-1];//1行 
	 			}
	 			a[r*N + i + r - 1] = a[r*N + i + r - 1] - temp;
				temp = 0;
	 			count = 0; 
	 			
	 			for( k=0; k= i)
			c[i*N + j] = a[i*N + j]; 
			else
			c[i*N + j] = 0;
			printf("%8.2lf",c[i*N + j]);
		}
		printf("\n");
	}
	printf("\n");
	for(i=0; i=0; i--){
	 	sum = 0;
	 	for(j=i+1; j

程序运行结果：如图二：

图二