实验5 遗传算法求解tsp问题

传送门（所有的实验都使用python实现）

实验1 BP神经网络实验

实验2 som网实验

实验3 hopfield实现八皇后问题

实验4 模糊搜索算法预测薄冰厚度

实验5 遗传算法求解tsp问题

实验6 蚁群算法求解tsp问题

实验7 粒子群优化算法求解tsp问题

实验8 分布估计算法求解背包问题

实验9 模拟退火算法求解背包问题

实验10 禁忌搜索算法求解tsp问题

 

 

一、实验目的

理解并使用遗传算法

二、实验内容

实现基于遗传算法的旅行商路线寻找

三、实验环境

使用Python3.0 在 eclipse进行编辑

四、实验步骤

1、输入介绍：

    城市总数目为30，每个城市的坐标以（x，y）表示，x，y的取值均为0~30的随机数。

2、初始群体设定：

随机产生n条长度为m的数组。n代表个体数目，m代表城市个数。在本次实验中设定n=10，m=30。且同一个体中的m个数互不相同，因为每个城市只经过一次。

4、适应度计算

    根据两点之间的距离公式可得n与m的距离

   

    将城市之间的相邻距离相加，总和越小的个体适应度越高。

 

5、选择算子

    采用最优保存策略，最优的个体直接覆盖最差个体，且这两个个体不参与交叉变异运算。

6.交叉算子

    采用有序交叉法，产生新个体。

7.变异

    对于变异的个体，在序列上随机出a,b两点，并将两点之间的序列倒置。

8.终止条件

    分别进行100,500,2000,10000次进化后终止。

 

 

 

 

 

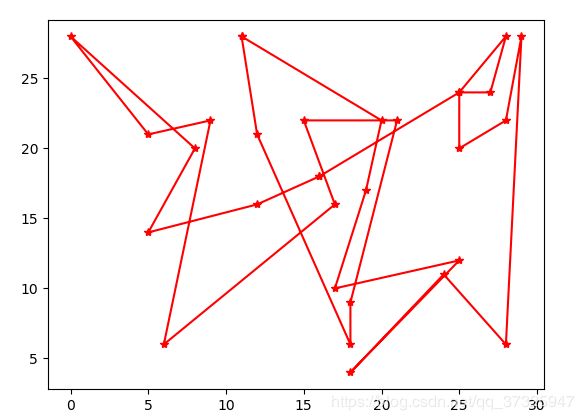
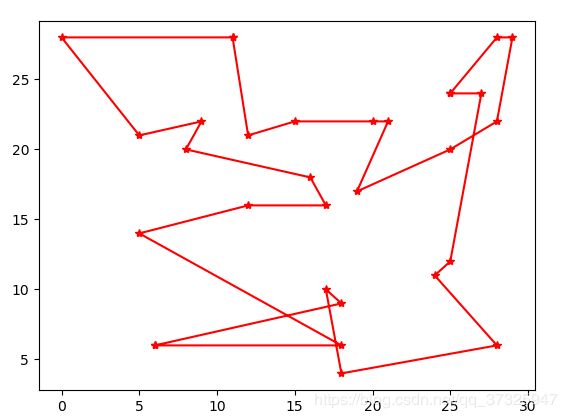
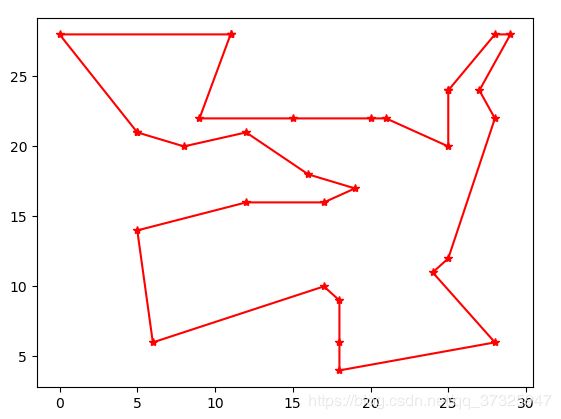
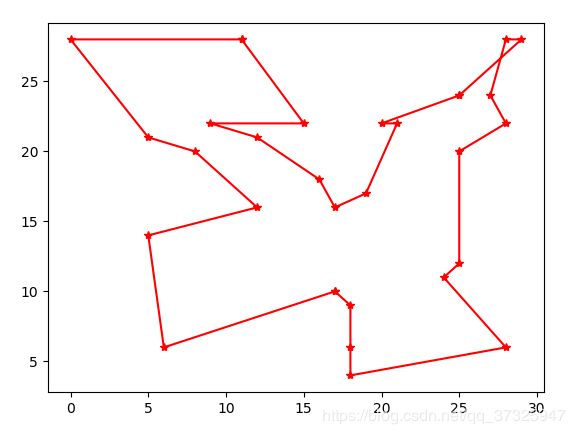
运行截图：

 

100次进化：总距离：240.883

 

500次进化总距离：172.05

 

 

2000次进化总距离：143.708

 

 

 

 

10000次进化总距离：142.136

五、总结

   

种群的初始个体数目设置的越多，产生的个体种类就越多，进而在比较少的进化次数中就能找到较优解，但是单次进化的时间会变长。此外变异因子不同值也会影响进化的进程。在本次实验中可以看到刚开始最优解变化很快，到2000次时开始趋于稳定。

Python源码

#coding:gbk
import random
import math
import matplotlib.pyplot as plt
global n,m,pc,pm,best;
pc = 0.9;pm=0.2;     #pc为交配概率 pm为变异概率
best = 10000;           #best记录最优距离，初始化无限大
n=10;m=30;          #n:样本个数    m:城市个数
dna = [[0]*(m) for i in range(n)]   #开辟n*m的数组
value = [0.0]*n;                        #value数组记录个体适应度
way =[0]*m;                          #way数组记录最优解路线
class no:                       #该类表示每个点的坐标
    def __init__(self,x,y):
        self.x=x;
        self.y=y;
p=[];
def draw(t):              #该函数用于描绘路线图
    x=[0]*(m+1);y=[0]*(m+1);
    for i in range(m):
        x[i] =p[t[i]].x;
        y[i] =p[t[i]].y;
    x[m] =p[t[0]].x;
    y[m] =p[t[0]].y;
    plt.plot(x,y,color='r',marker='*' ); 
    plt.show();
   
def  variation(x):   # 变异操作函数
    x1 = [0]*m;
    for i in range(m):
        x1[i] = x[i];
    a =random.randint(0,m-1);    #随机出两个点进行倒置
    b = random.randint(0,m-1);
    if(a > b): a,b=b,a;
    le = b-a+1;
    for i in range(le):
        x[a+i]=x1[b-i];
def  mycol():                           #城市坐标输入
        p.append(no( 8 , 20 ));
        p.append(no( 28 , 6 )); p.append(no( 27 , 24 )); p.append(no( 25 , 20 )); p.append(no( 5 , 14 )); p.append(no( 18 , 4 )); p.append(no( 21 , 22 ));
        p.append(no( 19 , 17 )); p.append(no( 28 , 22 )); p.append(no( 16 , 18 )); p.append(no( 28 , 28 )); p.append(no( 11 , 28 )); p.append(no( 29 , 28 ));
        p.append(no( 15 , 22 )); p.append(no( 25 , 24 )); p.append(no( 9 , 22 )); p.append(no( 17 , 16 )); p.append(no( 12 , 16 )); p.append(no( 5 , 21 ));
        p.append(no( 6 , 6 )); p.append(no( 12 , 21 )); p.append(no( 11 , 28 )); p.append(no( 20 , 22 )); p.append(no( 17 , 10 )); p.append(no( 18 , 6 ));
        p.append(no( 18 , 9 )); p.append(no( 25 , 24 )); p.append(no( 24 , 11 )); p.append(no( 25 , 12 )); p.append(no( 0 , 28 ));

def   init():        #初始化函数 随机产生初始个体
    vis = [0]*m;
    num=0;
    for i in range(n):
        for j in range(m):
            vis[j] = 0;
        for j in range(m):      
            num = random.randint(0,m-1);
            while(vis[num] == 1):
                num = random.randint(0,m-1);
            vis[num]=1;dna[i][j]=num;
def get_value(t):        #适应度计算
    ans = 0.0;
    for i in range(1,m):     #两点距离公式
        ans += math.sqrt((p[t[i]].x-p[t[i-1]].x) *(p[t[i]].x-p[t[i-1]].x)  +(p[t[i]].y-p[t[i-1]].y) *(p[t[i]].y-p[t[i-1]].y));
    ans +=  math.sqrt((p[t[0]].x-p[t[m-1]].x) * (p[t[0]].x-p[t[m-1]].x)  +(p[t[0]].y-p[t[m-1]].y) *(p[t[0]].y-p[t[m-1]].y));
    return ans;
def find(x,a,b,num):     #交叉算子运算时判断是否出现重复的城市id 
    for i in range(a,b+1):
        if(num[i] == x):
            return i;
    return -1;
    
def swap(x, y):         #有序交叉法
    x1 =  [0]*m;  y1 =  [0]*m;
    for i in range(m):
        x1[i]=x[i];y1[i]=y[i];
    a =  random.randint(0,m-1);    #随机产生两个点
    b = random.randint(0,m-1);
    if(a > b): a,b=b,a;
    for i in range(a):      #交叉运算
        x1[i]=y[i];y1[i]=x[i];
    for i in range(b+1,m):
        x1[i]=y[i];y1[i]=x[i];
    ob = 0;
    for i in range(m):       #判断交叉的合法性并进行维护，直到交叉成功
        if(i>= a and i<= b):
            continue;
        ob = find(x1[i],a,b,x1);
        while(ob != -1):
            x1[i] = y1[ob];
            ob = find(x1[i],a,b,x1);
    for i in range(m):     #操作同上，维护另一新个体的交叉合法性。
        if(i>= a and i<= b):
            continue;
        ob = find(y1[i],a,b,y1);
        while(ob != -1):
            y1[i] = x1[ob];
            ob = find(y1[i],a,b,y1);
    for i in range(m):
        x[i]=x1[i];y[i]=y1[i];
     
def slove():         #总执行函数
    global best;    #记录最短距离
    for i in range(n):
        value[i]=get_value(dna[i]);
    max_id = value.index(max(value));   #最优解与最差解个体的id被记录
    min_id = value.index(min(value));
    if(value[min_id] < best):
        best = value[min_id];
        for i in range(m):
            way[i] = dna[min_id][i];
    value[max_id] = value[min_id];  #最优解覆盖最差解
    fa = -1;
    for i in range(m):            
        dna[max_id][i]=dna[min_id][i];
    for i in range(n):                #开始交配
        if(random.random()> pc or i == max_id or i == min_id):
            continue;
        if(fa == -1):
            fa = i;
        else :
            swap(dna[fa], dna[i]);
            fa = -1;
    for i in range(n):              #变异运算
        if(random.random()> pm or i == max_id or i == min_id):
            continue;
        variation(dna[i]);

mycol();            #数据输入    
init();                 #群体初始化
for i in range(1000):      #控制进化次数
    slove();
draw(way);                      #画图描绘路线
print(round(best,3));       #打印距离
print(way);                     #打印路线，以序列表示