FFT(快速傅里叶变换)与NTT(快速数论变换)详解（11000+请耐心阅读）

参考自tly大佬与mys大佬的博客：友链：

orz tly大佬

orz mys大佬（他的博客似乎在某个我不知道的地方QAQ…其实看到他的博客是找他要的pdf版本）

也有一部分来自讲课时的课件。

Part.1 前置芝士

多项式的表示方法

多项式的表示方法分为两种，一种是系数表达法，另一种是点值表达法。

系数表达法

就是常见的解析式了，一般的多项式表示成$f(x)=a_0+a_{1}x+a_2{x}^2+\cdots a_n{x}^n={\sum }_{i=0}^N{a}_i{x}^i$。

点值表达法

对于一个多项式$f(x)={\sum }_{i=0}^N{a}_i{x}^i$，我们选取$n+1$个不同的$x_i$带进去，得到了$n+1$个$y_i$，这样用$n+1$个数对$(x_i,y_i)$就可以表示一个多项式了。

不难发现一个点值表示唯一对应一个多项式，但一个多项式就能够对应多个点值表示了。

点值表示的性质

对于两个多项式$f(x),g(x)$，我们把$\{x_1,x_2,x_3,\dots ,x_n\}$代进去，得到了$f(x),g(x)$的点值表示：$\{(x_1,f(x_1)),(x_2,f(x_2)),(x_3,f(x_3)),\dots ,(x_n,f(x_n))\}$和$\{(x_1,g(x_1)),(x_2,g(x_2)),(x_3,g(x_3)),\dots ,(x_n,g(x_n))\}$。

那么不难发现$f(x)\cdot g(x)$的点值表示其实就等于$\{(x_1,f(x_1)g(x_1)),(x_2,f(x_2)g(x_2)),(x_3,f(x_3)g(x_3)),\dots ,(x_n,f(x_n)g(x_n))\}$。

这样一来，我们只要取足够多的$x_i$，就可以按照如下方式将两个多项式乘起来：

1. 选取足够多的值代入两个多项式$f(x),g(x)$中，得到它们的点值表示；
2. 将两个多项式的点值表示对应项乘起来；
3. 将得到的点值表示还原成系数表示。

但这样做看上去对原来$O(n^2)$的多项式乘法似乎没什么优化，但没错，接下来，FFT将把这个过程优化到$O(n\log n)$。

Part.2 傅里叶变换

如何将算法优化到$O(n\log n)$？

这意味着我们需要选取一些特殊的值代进去。

这种值就叫单位复根。

补充：单位复根

单位复根的实质是复数。

复数

复数是形如$a+bi$的一种数，其中$i=\sqrt{-1}$。称此时的$a$为实部，$b$为虚部。

它可以在二维坐标系中表示，它表示为一个向量。

称此时它的长度为模长，与$x$轴（实数轴）的夹角为幅角。

这样一来，复数的乘法就是模长相乘，幅角相加。

单位复根

使得${\omega }^n=1$的复数$\omega$为$n$次单位复根。

不难发现$n$次单位复根恰好有$n$个，它们是$e^{\frac{2\pi ik}{n}},k=0,2,\dots ,n-1$。

复数的幂$e^{i\theta }=\cos \theta +\sin \theta i$。

称此时的${\omega }_n=e^{\frac{2\pi i}{n}}$为主$n$次单位复根，其他的$n$次单位复根都是主单位复根的幂。

这样一来，单位复根就有了一些性质：

• $|{{\omega }_n}^i|=1$；
• ${{\omega }_n}^i$的幅角为$\frac{2\pi i}{n}$；
• ${{\omega }_n}^n={{\omega }_n}^0$，也就是说$n$次单位复根最多有$n$个，分别是${{\omega }_n}^0,{{\omega }_n}^1,{{\omega }_n}^2\dots ,{{\omega }_n}^{n-1}$。

单位复根的数学性质

其实单位复根还有一些其他的数学性质：（这些性质都可以通过画图来证明）

相消引理

若$d>0$，则有${{\omega }_{dn}}^{dk}={{\omega }_n}^k$。

证明（推式子）：${{\omega }_{dn}}^{dk}=(e^{\frac{2\pi i}{dn}}{)}^{dk}=(e^{\frac{2\pi i}{n}}{)}^k={{\omega }_n}^k$。

它有一个推论：${{\omega }_{2n}}^n={\omega }_2=-1$。

折半引理

${{\omega }_{2n}}^k=-{{\omega }_{2n}}^{k+n}$。

证明就是将等式两边平方后发现它的值对应相等，而方向相反。

求和引理

对于不能被$n$整除的数$k$有${\sum }_{j=0}^{n-1}({{\omega }_n}^k{)}^j=0$。

证明：不难发现这是一个等比数列，应用等比数列的求和公式可得：${\sum }_{j=0}^{n-1}({{\omega }_n}^k{)}^j=\frac{({{\omega }_n}^k{)}^n-1}{{{\omega }_n}^k-1}=\frac{1^k-1}{{{\omega }_n}^k-1}=0$。

傅里叶正变换

我们选取$n$次单位复根代入$n-1$次多项式。

为了加快运算，我们将多项式的奇次项和偶次项分开来算，最后将它们组合在一起。

记多项式$f(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}$。

将其分成两个多项式：$f^{[0]}(x)=a_0+a_{2}x+a_4{x}^2+\cdots ,f^{[1]}(x)=a_1+a_{3}x+a_5{x}^2+\cdots$。

则不难得出$f(x)=f^{[0]}(x^2)+x{f}^{[1]}(x^2)$。

我们取$n=2p$，将${{\omega }_n}^k$和${{\omega }_n}^{k+p}$代入多项式得到：

$f({{\omega }_n}^k)=f^{[0]}(({{\omega }_{\frac{n}{2}}}^{\frac{k}{2}}{)}^2)+{{\omega }_n}^k{f}^{[1]}(({{\omega }_{\frac{n}{2}}}^{\frac{k}{2}}{)}^2)=f^{[0]}({{\omega }_p}^k)+{{\omega }_n}^k{f}^{[1]}({{\omega }_p}^k)$

$f({{\omega }_n}^{k+p})=f^{[0]}({{\omega }_p}^{\frac{k}{2}})+{{\omega }_n}^{k+p}{f}^{[1]}({{\omega }_p}^{k+p})=f^{[0]}({{\omega }_p}^k)-{{\omega }_n}^k{f}^{[1]}({{\omega }_p}^k)$

就像上面两个式子一样，只要我们知道了$f^{[0]}({{\omega }_p}^k)$和$f^{[1]}({{\omega }_p}^k)$，就可以$O(1)$的算出$f({{\omega }_n}^k)$和$f({{\omega }_n}^{k+p})$。

因此，只要我们递归的求解$f^{[0]}({{\omega }_p}^k)$和$f^{[1]}({{\omega }_p}^k)$，就可以在$O(n)$的时间内算出$f(x)$的点值表示。

时间复杂度为$O(n\log n)$。

迭代实现傅里叶正变换

递归版本的FFT虽然将计算多项式点值表示的时间复杂度降到了$O(n\log n)$，但一个显然的问题是这个算法的常数太大了。

我们考虑将整个奇偶分组后各个系数数的位置：

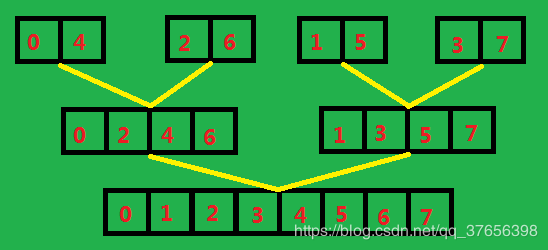
原来的序列：0,1,2,3,4,5,6,7。

变换后的序列：0,4,2,6,1,5,3,7。

将它们变成二进制：

原序列：000,001,010,011,101,110,111。

变换后的序列000,100,010,110,101,011,111。

这样我们就发现它们的值就是二进制位的反转。

我们将系数中该换位置的都换了，倒着做FFT就够了。

如何获得二进制位的反转呢？只要简洁就行了。具体还是参考代码吧。

多项式点值表示->系数表示：傅里叶逆变换

但我们获得了点值表示，如果我们要将它变成系数表示呢？

观察FFT的实质，我们进行了一次矩阵乘法：

$$\left[\begin{array}{ccccc}({{\omega }_n}^0{)}^0& ({{\omega }_n}^0{)}^1& ({{\omega }_n}^0{)}^2& \cdots & ({{\omega }_n}^0{)}^{n-1}\\ ({{\omega }_n}^1{)}^0& ({{\omega }_n}^1{)}^1& ({{\omega }_n}^1{)}^2& \cdots & ({{\omega }_n}^1{)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ ({{\omega }_n}^{n-1}{)}^0& ({{\omega }_n}^{n-1}{)}^2& ({{\omega }_n}^{n-1}{)}^3& \cdots & ({{\omega }_n}^{n-1}{)}^{n-1}\end{array}\right]\times \left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]=\left[\begin{array}{c}f({{\omega }_n}^0)\\ f({{\omega }_n}^1)\\ ⋮\\ f({{\omega }_n}^{n-1})\end{array}\right]$$

记上面的系数矩阵（第一个矩阵）为$V$。

对于另一个矩阵$D=\left[\begin{array}{ccccc}({{\omega }_n}^{-0}{)}^0& ({{\omega }_n}^{-0}{)}^1& ({{\omega }_n}^{-0}{)}^2& \cdots & ({{\omega }_n}^{-0}{)}^{n-1}\\ ({{\omega }_n}^{-1}{)}^0& ({{\omega }_n}^{-1}{)}^1& ({{\omega }_n}^{-1}{)}^2& \cdots & ({{\omega }_n}^{-1}{)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ ({{\omega }_n}^{-n+1}{)}^0& ({{\omega }_n}^{-n+1}{)}^2& ({{\omega }_n}^{-n+1}{)}^3& \cdots & ({{\omega }_n}^{-n+1}{)}^{n-1}\end{array}\right]$

考虑$D\times V$：

$$\begin{array}{rl}(D\times V{)}_{i,j}& =\sum _{k=1}^{n-1}{D}_{i,k}\cdot V_{i,k}\\ & =\sum _{i=1}^{n-1}{{\omega }_n}^{-ik}\cdot {{\omega }_n}^{jk}\\ & =\sum _{k=1}^{n-1}{{\omega }_n}^{(j-i)k}\end{array}$$

当$i=j$时，$$\begin{array}{rl}(D\times V{)}_{i,j}& =\sum _{k=1}^{n-1}{{\omega }_n}^{(j-i)k}\\ & =\sum _{k=1}^{n-1}{{\omega }_n}^0\\ & =n\end{array}$$

当$i\ne j$时，$$\begin{array}{rl}(D\times V{)}_{i,j}& =\sum _{k=1}^{n-1}{{\omega }_n}^{(j-i)k}\\ & =1+({{\omega }_n}^{j-i}{)}^1+({{\omega }_n}^{j-i}{)}^2+\cdots +({{\omega }_n}^{j-i}{)}^{n-1}\\ & =\frac{1-({{\omega }_n}^{j-i}{)}^n}{1-{{\omega }_n}^{j-i}}\\ & =0\end{array}$$

于是$$D\times V\times \left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]=\left[\begin{array}{ccccc}n& 0& 0& \cdots & 0\\ 0& n& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & n\end{array}\right]\times \left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]=\left[\begin{array}{c}n{a}_0\\ n{a}_1\\ ⋮\\ n{a}_n\end{array}\right]$$

所以再给我们得到的点值表示乘上这个矩阵$D$，每个值除以$n$后就得到了多项式的系数表示。

FFT完整模板

代码中定义了复数类，方便运算。

好像STL里面也有一个复数类，但似乎跑得有点慢。

顺便提一句，由于FFT要求所代入的多项式必须是2的整数次幂，所以我们将多项式的项数扩充到了2的整数次幂。

const double PI = 3.1415926535;

struct Complex {
	double a, b;
	Complex(double x = 0, double y = 0) {a = x, b = y;}
	Complex operator + (const Complex &rhs) const {return Complex(a + rhs.a, b + rhs.b);}
	Complex operator - (const Complex &rhs) const {return Complex(a - rhs.a, b - rhs.b);}
	Complex operator * (const Complex &rhs) const {return Complex(a * rhs.a - b * rhs.b, a * rhs.b + b * rhs.a);}
};
int rev[Maxsize + 5];
void GetReverse(int len, int l) {
	for(int i = 0; i < len; i++)
		rev[i] = 0;
	for(int i = 0; i < len; i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (l - 1));
}
inline Complex EXP(double theta) {
	return Complex(cos(theta), sin(theta));
}
void FFT(vector<Complex> &a, int dir) {
	int len = a.size();
	for(int i = 0; i < len; i++)
		if(i < rev[i]) swap(a[i], a[rev[i]]);
	for(int stp = 1; stp < len; stp <<= 1)
		for(int k = 0; k < stp; k++) {
			Complex wk = EXP(dir * k * PI / stp);
			for(int even = k; even < len; even += stp << 1) {
				int odd = even + stp;
				Complex tmp = a[odd] * wk;
				a[odd] = a[even] - tmp;
				a[even] = a[even] + tmp;
			}
		}
	if(dir == -1)
		for(int i = 0; i < len; i++)
			a[i].a /= len;
}

Part.3 NTT快速数论变换

不难发现FFT中大量用到了实数的运算和三角函数，这会导致精度、常数等问题。

我们是否可以在模意义下找到一种数，使得这些都满足单位复根的性质？

想一想我们用到的单位复根的性质：

1. ${{\omega }_n}^i\times {{\omega }_n}^j={{\omega }_n}^{i+j}$；
2. （相消引理）${{\omega }_{dn}}^{dk}={{\omega }_n}^k$；
3. （折半引理）${{\omega }_{2n}}^k=-{{\omega }_{2n}}^{k+n}$；
4. $n$个数互不相同且有${{\omega }_n}^0=1$。

换句话说，我们要找出一种数，要求在模意义下满足上述条件。

单位复根的替代——原根

原根的性质

对于一个素数$P$，若有一个数$G$使得$G^1,G^2,G^3,\dots ,G^{p-2}(\mathrm{m}\mathrm{o}\mathrm{d}P)$互不相同，则$G$是$P$的一个原根。

再定义${g_n}^k=(G^{\frac{P-1}{n}}{)}^k$，检验一下是否满足上述性质。

1. 由幂的运算可知显然成立；
2. 由幂的运算可知显然成立；
3. ${g_{2n}}^{n+k}=(G^{\frac{P-1}{2n}}{)}^{n+k}=(G^{\frac{P-1}{2n}}{)}^n\cdot (G^{\frac{P-1}{2n}}{)}^k=G^{\frac{P-1}{2}}\cdot {g_{2n}}^k\equiv -{g_{2n}}^k(\mathrm{m}\mathrm{o}\mathrm{d}P)$【因为$G^{p-2}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}P)$，又因为$G$是$P$的原根即$G^{P-1}\not\equiv G^{\frac{P-1}{2}}(\mathrm{m}\mathrm{o}\mathrm{d}P)$，故有$G^{\frac{P-1}{2}}\equiv -1(\mathrm{m}\mathrm{o}\mathrm{d}P)$】；
4. 由原根的定义可得。

然后就是将所有涉及到复数运算的部分全部替换成原根即可。

NTT的特殊要求

你以为将单位复根换成原根就完了？

事实上，我们知道FFT需要将多项式的项数扩充到二的整数次幂，而NTT也一样。

换句话说，NTT的模数的$P$应该满足$P=k\times 2^m+1$，例如常用的模数$998244353=7\times 17\times 2^{23}+1$。

如果记不住原根可以按文章末尾的方法求出。

NTT完整模板

const int Mod = 998244353;
const int G = 3;

int QuickPow(int a, int k) {
	int ret = 1;
	while(k) {
		if(k & 1) ret = 1LL * ret * a % Mod;
		a = 1LL * a * a % Mod;
		k >>= 1;
	}
	return ret;
}

int rev[Maxsize + 5];
inline void GetReverse(int len, int lg) {
	for(int i = 0; i < len; i++) rev[i] = 0;
	for(int i = 0; i < len; i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (lg - 1));
}
void NTT(vector<int> &a, int dir) {
	int len = a.size();
	for(int i = 0; i < len; i++)
		if(i < rev[i]) swap(a[i], a[rev[i]]);
	int g = (dir == 1 ? G : QuickPow(G, Mod - 2));
	for(int stp = 1; stp < len; stp <<= 1) {
		int wn = QuickPow(g, (Mod - 1) / (stp << 1));
		int w = 1;
		for(int k = 0; k < stp; k++) {
			for(int even = k; even < len; even += stp << 1) {
				int odd = even + stp;
				int tmp = 1LL * w * a[odd] % Mod;
				a[odd] = (a[even] - tmp + Mod) % Mod;
				a[even] = (ll)(a[even] + tmp) % Mod;
			}
			w = 1LL * w * wn % Mod;
		}
	}
	if(dir == -1) {
		int inv = QuickPow(len, Mod - 2);
		for(int i = 0; i < len; i++)
			a[i] = 1LL * a[i] * inv % Mod;
	}
}

补充：原根的求法

如何求一个奇素数$p$的原根？

常用的方法是先将$p-1$唯一分解成$p_1^{k_1}{p}_2^{k_2}\cdots p_m^{k_m}$。

然后再暴力枚举原根，对于一个数$g$，只要满足对于$p-1$的任意一个质因数都有$g^{\frac{p-1}{p_i}}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}P)$成立，那么这个数就是原根。

一般的数的原根都不大，直接枚举即可。

补充：NTT常用模数及其原根表

参考自：https://blog.csdn.net/hnust_xx/article/details/76572828

对于NTT的模数$P=k\times 2^m+1$列出常用的部分和它们的原根。

$P=k\times 2^m+1$	$k$	$m$	$g$
3	1	1	2
5	1	2	2
17	1	4	3
97	3	5	5
193	3	6	5
257	1	8	3
7681	15	9	17
12289	3	12	11
40961	5	13	3
65537	1	16	3
786433	3	18	10
5767169	11	19	3
7340033	7	20	3
23068673	11	21	3
104857601	25	22	3
167772161	5	25	3
469762049	7	26	3
998244353	119	23	3
1004535809	479	21	3
2013265921	15	27	31
2281701377	17	27	3
3221225473	3	30	5
7516927681	35	31	3
77309411329	9	33	7
206158430209	3	36	22
2061584302081	15	37	7
2748779069441	5	39	3
6597069766657	3	41	5
39582418599937	9	42	5
79164837199873	9	43	5
263882790666241	15	4	7
1231453023109121	35	45	3
1337006139375617	19	46	3
3799912185593857	27	47	5
4222124650659841	15	48	19
7881299347898396	7	50	6
31525197391593473	7	52	3
180143985094819841	5	55	6
1945555039024054237	27	56	5
4179340454199820289	29	57	3