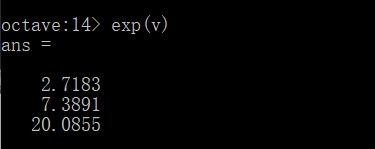Octave 计算数据

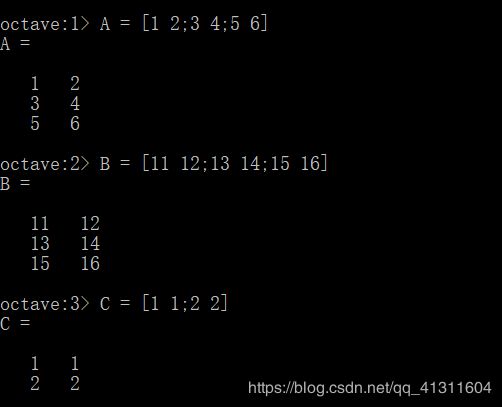
首先，先快速初始化几个变量。设A为1个 3 x 2的矩阵，设B为1个3 x 2的矩阵，并设C为1个2 x 2的矩阵。

 

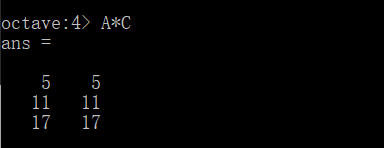
现在来计算两个矩阵的乘积，比如计算A X C，只需要键入A*C，那么1个3 x 2的矩阵与1个2 x 2的矩阵，得到的就是一个3 x 2的矩阵。

 

你也可以对元素进行运算。输入A .* B，这样的话，会将A中的各个元素与B中对应的元素相乘。通常，这个点号，一般用于表示元素的运算。

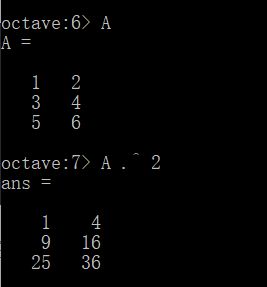
如果输入A .^ 2，就会对A中的每个元素进行乘方。

 

现在设v是一个列向量，可以输入1 ./ v ，来求得v的每个元素的倒数。

 

同样也可以对矩阵使用，输入 1 ./ A ，会得到A中所有元素的倒数。

 

同样的这里的点号代表进行的是元素的运算。

 

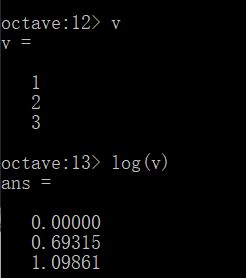
还可以用log(v)，对v的所有元素进行求对数运算。

 

而exp(v)，就是以e为底，v中的元素作为幂指数的幂运算。

 

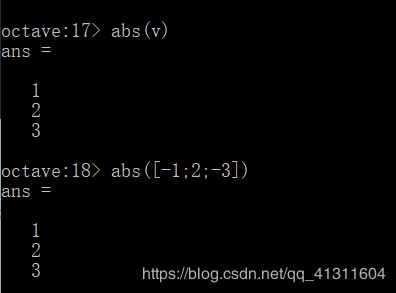
另外，还可以用abs(v)，来求得v中所有元素的绝对值。

 

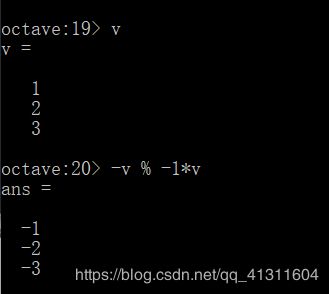
如果输入-v，会得到v中所有元素的相反数，这等价于-1乘以v，但是一般写成-v就可以了。

 

这里有个小技巧，如果想取出v，并对v中的每个元素都加1，其中一个方法就是构造一个3 x 1的元素全部为1的向量，然后将这个向量与v相加，这样做的话，会使v从[1;2;3]增加到[2;3;4]。

这样做是因为，length(v)的值为3，所以ones(length(v),1)相当于令ones的大小为3 x 1，然后让v和ones相加，于是v中的各个元素都加上了ones中的对应元素，也就是都加上了1。

 

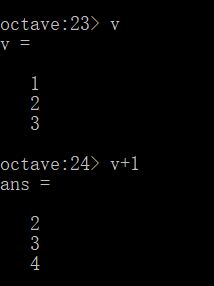
令一种更简单的方法是，直接输入v+1，同样也能对v中的每个元素对应都加1。

 

再来看一些其他的运算。

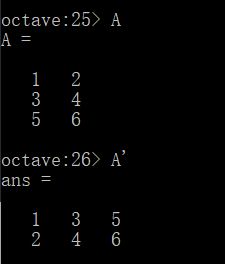
如果想求一个矩阵的转置矩阵，可以键入 A'  

 

如果要求A的转置的转置，那么很明显，也就会得到A本身。

 

还有一些有用的函数。先建立一个1行4列的矩阵a，设val = max(a)，这样将返回a中最大的元素：

 

还可以设 [ val, ind] = max(a)   这将返回两个值，val是a中的最大元素，ind是a中该元素的索引。即a中的第2个元素为最大元素，该元素为15。

 

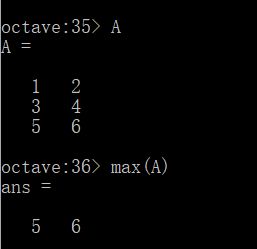
但是如果A是一个矩阵，那么输入max(A)就要特别注意。这样做的话实际上会得到每一列的最大值。这一点稍后再来深入讨论。

 

先来看这个例子。设a = [1 15 2 0.5]，然后输入a < 3  ，这实际上称为对应元素比较，它将会将a中的每个元素逐个与3进行比较，如果<3，对应位置返回1（表示真），否则返回0（表示假）。

 

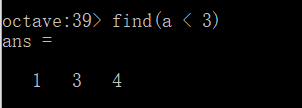
现在如果输入find(a < 3)，这将找出a中所有小于3的元素，并返回它们的索引。

 

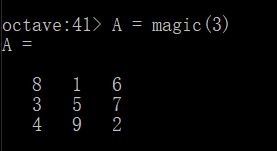
我们又来看下一个例子，如果设A = magic(3)，magic函数会返回什么呢？

 

我们可以通过输入 help magic 查询一下。magic函数会返回名为幻方的矩阵。幻方具有一种特殊的数学性质。它的任意行、列、对角线中的元素加起来都等于相同的值，虽然这个函数在机器学习里用处不大，但是可以很便捷地生成一个矩阵。

 

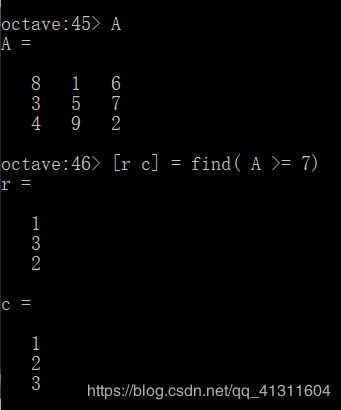
如果输入[r c] = find(A >= 7)   就会找出A中大于等于7的元素，r和c分别表示这些大于等于7的元素所在的行索引和列索引。

例如第1行第1列的元素大于等于7，第3行第2列的元素大于等于7，第2行第3列的元素大于等于7。

 

下面将一个求和函数，有一个矩阵a，输入sum(a)   就会得到a中所有元素的和。如果想求a中所有元素的乘积，输入prod(a)，prod也就是product 乘积这个单词的缩写。

 

floor(a)可以对a中所有的元素向下取整（floor这个单词有地板的意思，所以可以记忆为向地板方向取整，也就是向下取整）。

 

而ceil(a)会对a中的所有元素向上取整（ceil有天花板的意思，所以可以及一位向天花板方向取整，也就是向上取整）。

 

如果输入rand(3)，会得到一个3  x 3的随机矩阵：

 

而如果输入max(rand(3),rand(3))会返回这样一个矩阵，它由两个3 x 3的随机矩阵对应位置进行逐个比较，每个位置取较大的元素组成。

 

现在有一个矩阵A，如果输入max(A,[],1)  这样会得到每一列的最大值。这里的1表示从A的第一维度去取值。

 

对应地，如果输入max(A,[],2)  就能得到每一行的最大值。

 

通过这种方法就能求得每行或每列的最值。另外需要记住max(A)默认是求每列的最大值。而如果只想求整个矩阵A的最大值，可以输入max(max(A))

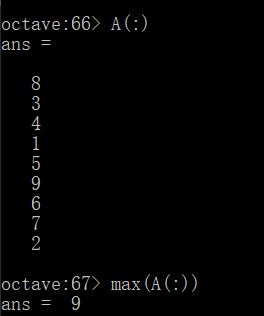
或者也可以先将A变成一个向量。也就是可以输入max(A(:))，相当于把A当做一个向量，然后求这个向量的最大元素。

 

最后，让我们把A设为一个9x9的幻方。幻方的特性是幻方的每列、每行加起来都是一样的，包括对角线。

现在如果输入sum(A,1)  就可以求得每一列的和，输入sum(A,2)  就可以得到A中每一行的和。

可以看到它的各行各列加起来都是369，这也验证了幻方的性质。

 

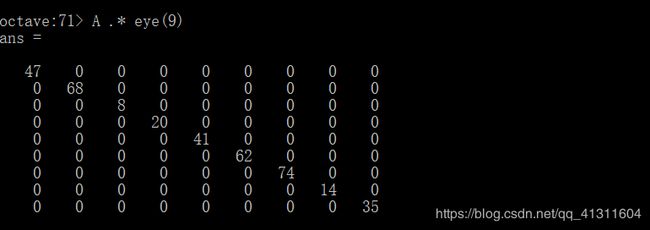
现在来计算A的对角线元素，以确保它们加起来也等于369。那么需要先构造一个9阶的单位矩阵。让这个单位矩阵与A中的每个元素对应相乘，也就是点乘。这样做的结果是，除了对角线以外，其余元素都会乘0而得到0。

 

那么再输入sum(sum(A .* eye(9)))  就能得到A中对角线元素的和。

 

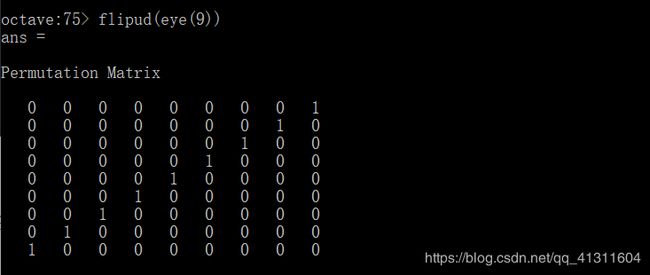
也可以求另一条对角线的和，输入sum(sum(A .* flipud(eye(9))))  flipud表示使矩阵垂直翻转。

 

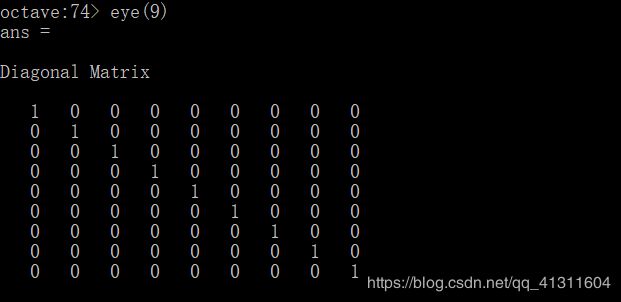
这是9阶的单位矩阵：

 

纵向翻转这个单位矩阵后得到的矩阵是：

 

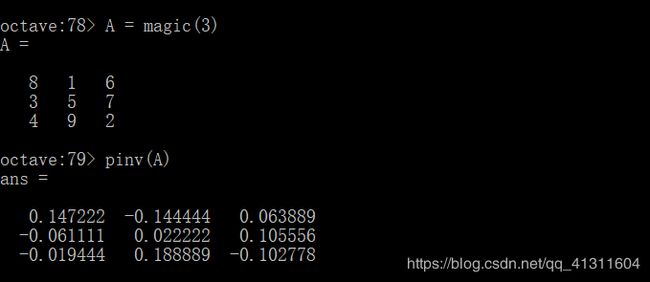
最后再说一个命令，假设A还是一个3阶的幻方，要求A的逆矩阵，键入piv(A)

 

这通常被称作伪逆矩阵，但这并不要紧，你可以把它看做是对A求逆，因此这就是A的逆矩阵。

我们设temp = pinv(A)，再用temp*A，得到的就是单位矩阵。