详解Huffman压缩原理和c++代码实现
写在前面
Huffman压缩原理其实挺好理解的,我用java很快就写好了。然后用c++写,一开始我是这么想的:c++偏底层,应该对二进制串文件的读写会更简单吧。
不涉及到文件读写的部分确实很快就做好了,然后就被文件读写折磨。
各种深夜痛哭... ...
但还是值得的,学习了更多底层的知识。我对Huffman压缩基本掌握了。(本来想说完全掌握的,但,呵,生活。微笑)
写这篇博客花了我很长时间,我完全尽力了。我尽可能详细地写了三部分,分别是Huffman原理、坑和c++代码实现。我举了一些例子,并且经过实际动手验证,还自行绘制了几幅图帮助理解。
欢迎指错和讨论交流,也欢迎提问质疑,尽管能力有限,但我尽力解答。
目录
一、Huffman压缩
1、文件在计算机中存储形式
2、Huffman压缩算法原理
3、例子解析
二、需要特别注意的坑
1、windows的'\r\n'问题,c/c++可以用二进制方式读取来解决
2、文件读取末尾问题
三、Huffman的实现(上代码,本文c++版本,如果要java版本请私聊我)
编码篇
1、统计频率
2、建立Huffman树
3、获取Huffman编码表
4、编码
译码篇
1、获取Huffman译码表
2、译码
正文
一、Huffman压缩
1、文件在计算机中存储形式
在开始实现之前,我们要了解下计算机底层的编解码。
计算机只认0与1,一切文件最终的存储形式都是0、1串。文本、图片、视频等文件都是通过一定的协议进行编解码,而 这些协议及其转化由各种各样的软件(音频软件、画图软件、记事本等)实现。 下图是一张png图片文件在计算机中存储形式, 可以通过Binary Viewer 软件进行查看。
文件的存储有定长存储和不定长存储,定长存储就是int、char、byte等类型会以固定的位数b进行存储。举个例子,我们新建txt文件,写入“4 中”然后敲回车换行,再写入“16”,保存。现在我们用Binary Viewer查看它在计算机中的存储。 ![]()
因为我们是用文本文件进行存储,所以记事本的编解码方式是将每一个字符对应的ASCII码写入文本文件,如果是0-127的只有8位,如果是中文这样的拓展字符则有16位。
我们看图吧,第一个字节(8位)“00110100”转化为10进制为52, 查ASCII表为‘4’,接下来的第二个字节“00100000”代表空格,接下来的两个字节是‘中’,然后依次是‘\r’,‘\n’,‘1’,6’。这里特别强调下,Windows系统用‘\r\n’表示换行,而Liunx用‘\n’,Mac用‘\r’。为什么会有如此差异呢?感兴趣的自行百度,这个跟早期打印机有关,现在只是一个规则,并没有实际含义,但要特别特别注意 。我写Huffman的时候被这个坑了,具体我们后面再说。我强烈建议写压缩的时候用上查看二进制串的工具(比如Binary Viewer),有利于理解和debug。
2、Huffman压缩算法原理
我们上边提到了计算机的定长存储,其实我们也看到了存储‘4’这样的数字,计算机用了8位,那么我们能不能减少二进制串呢,从而来实现压缩?有很多压缩算法,他们主要是用新一套的编解码表来实现。而每次所用的编码表都是不同的,是依据压缩的文件来决定的。
那Huffman是怎么做的呢?它先通过对要压缩的文件进行统计频率,比如在“65da as 美65a”中a-3(表示a出现3次),d-1,s-1,6-2,5-2,美-1,空格-2。Huffman采用不定长进行存储,频率高的对应的编码长度较短,频率低的对应的编码长度较长。但我们压缩后是要能解压的,假如有这样的一组编码“00101110”,Huffman压缩算法每次读取一位,直至找到在Huffman编码表中找到,然后去除这一串,接着重复以上操作,直至编码读取完毕。要实现这样的结果,我们要怎么创立Huffman编码表呢?以下是具体做法:(边看例子辅助理解)
(1)先对压缩文件的字符进行频率统计,以“字符--频率”的形式存入某容器m
(2) 在容器m中取出两个频率最小对应的字符,作为二叉树的两个叶子节点,并将频率和作为它们的根节点,同时将新结点存入容器m,将旧的两个结点踢出容器m。(容器m可以是优先队列)
(3)重复(2),直到最后容器m中只有一个元素。
(4) 将形成的二叉树的左节点标0,右节点标1。把从最上面的根节点到最下面的叶子节点途中遇到的0,1序列串起来,就得到了各个符号的编码。
3、例子解析
例子:有一串“cdbedfaabca”,进行Huffman编码和解码。
编码: (1)频率统计 f:1 e:1 d:2 c:2 b:2 a:5
(2) f与 e作为叶子结点,其根节点为_2 。 此时,新的频率表为:_2 d:2 c:2 b:2 a:5
d与_2作为叶子结点,其根节点为_4 。 此时,新的频率表为:c:2 b:2 _4 a:5
b与 c作为叶子结点,其根节点为_4 。 此时,新的频率表为:_4 _4 a:5
_4与_4作为叶子结点,其根节点为_8 。 此时,新的频率表为: _8 a:5
_8与 a作为叶子结点,其根节点为_13 。
结束。
(3)左子树标0,右子树标1。如下图所示:
Huffman编码表 a:0 c:100 b:101 f:1100 e:1101 d:111
那么“cdbedfaabca”的编码为“10011110111011111100001011000”。
解码: 读取第一位‘1’,搜索Huffman表,找不到。继续读下一位“10”,找不到,继续读下一位“100”,此时对应字符‘c’。
那么清零,继续读第一位“1”,直至读到“111”,对应‘d’。
继续清零,继续读第一位‘0’,直至读到“101”,对应‘b’。
... ...
读到最后,得“cdbedfaabca”。
二、需要特别注意的坑
1、windows的'\r\n'问题
c++在windows系统中,在读写文件时,有两种格式,分别是文本文件和二进制文件,它们的区别只有一点。
文本文件表示换行会用'\r\n',上文我们已经证明了,在txt文件换行后,用软件查看其二进制存储形式,发现换行是'\r\n'对应的Ascii码。也就是,写入时写入'\r\n',然后在读取时会把'\r\n'转化成换行。
你应该没意识到这对Huffman压缩有什么影响,那么我们举四个例子来进一步说明吧。
我用二进制形式写入‘\n’时,txt文本打开没有换行,也没有其它改变。但用c++读取时读到‘\n’,会换行。
我用二进制形式写入‘\r’时,txt文本打开没有换行,也没有其它改变。但用c++读取时读到‘\r’,没有任何操作。
我用二进制形式写入‘\r\n’时,txt文本打开换行。但用c++读取时只读到‘\n’,(没有读到'\r' !!!),会换行。
我用二进制形式写入‘\n\r’时,txt文本打开没有换行,也没有其它改变。用c++读取时读到‘\n\r’,会换行('\n'实现的)。
为什么要特意强调这点呢?
因为我们在进行Huffman压缩的过程中,我们可能会存储“11111111”(-1),“00001010”(\n),“00001101”(\r)这样比较特殊的字符。-1经常被用于证明文件读到末尾,\n、\r与换行关系密切。
事实证明,“11111111”并没有影响,即便程序读到了-1,它依然会继续读取,所以不需要考虑。
而根据上面的四个例子,读取到‘\n’,‘\r’,‘\n\r’时都不会有影响,但若是读取到‘\r\n’,恭喜你,出错了,这时候‘\r’不会被读取到。后果就是译码时会出错,译码到那里时就开始跟原文不同了。
怎么解决呢?
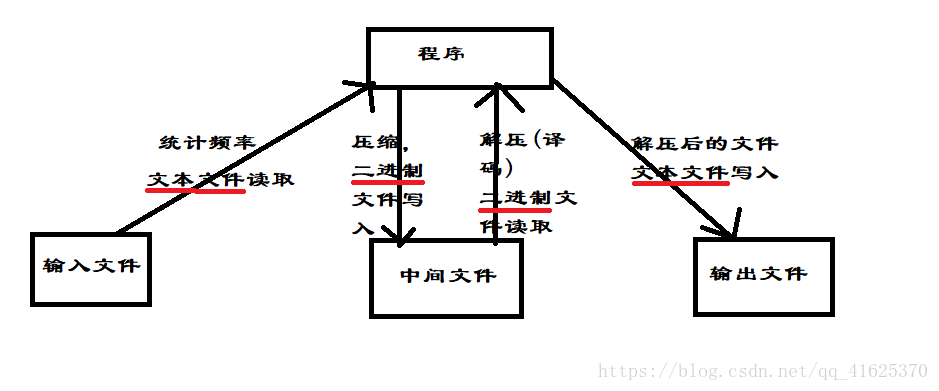
我给出的方案是:进行Huffman编码和译码时,避免使用文本文件来读写,采用二进制文件。在读取原文件和输出译码后的文件时,用文本文件,而不用二进制文件,这样才能保证文件打开时能正常显示换行。
如图:
2、文件读取末尾问题
读取文件判断末尾,c++用eof()或fail()方法都行,“11111111”并不会造成影响。
ifstream in("E:\fin.txt");
char ch;
while(!in.eof())
{
in.get(ch);
cout<但是有点问题,就是最后一个字符会被读取两次,这是因为当文件输入流读取不到时,它才会停止读取。所以当读取到最后一个字符时,in.eof()返回仍为false,所以会再执行in.get(ch),此时输入流指针读取不到,in.eof()才返回true。但ch未改变,导致文件最后一个字符会被读取两遍。
最简单的解决方案如下:
ifstream in("E:\fin.txt");
char ch;
while(!in.eof())
{
in.get(ch);
if(!in.eof()){ //再判断一次
cout<二、Huffman的实现(上代码)
编码篇
1、统计频率
//读取原文件,统计频率并加入map中
void read_count(const char* fin) //char * fin为文件路径
{
char ch;
string s;
ifstream in(fin);
if(!in.good())
{
printf("Cannot open the file %s\n",fin );
return ;
}
while(!in.eof())
{
in.get(ch);
//该判断用于避免读取不存在的下一位
if(!in.eof()){
s=ch;
//这种查找会增添新元素
map1[s]=map1[s]+1;
}
}
}2、建立Huffman树
以下部分为所有的全局变量(两条线以内)
============================================================================
#define MAX 100000
//huffman树 结点
struct Huffman
{
Huffman(string c,int n):num(n),ch(c),lchild(NULL),rchild(NULL) {}
Huffman():ch(""),lchild(NULL),rchild(NULL) {}
int num; //存储频数
string ch=""; //存储字符
Huffman *lchild; //左子树
Huffman *rchild; //右子树
};
typedef Huffman* Node;//比较器,用于优先队列
class Compare
{
public:
bool operator()(const Node& c1, const Node& c2) const
{
return (*c1).num > (*c2).num;
}
};//map映射,用于key与value的相互转化,进行编解密
mapmap1;
mapmap2;
mapmap3;
map::iterator l_it; //迭代器,用于map的遍历 //优先队列,辅助huffman树的建立
priority_queue< Node, vector, Compare > pq;
string str="";
string result=""; ============================================================================
//得到初始的优先队列
void getArray()
{
for(l_it = map1.begin(); l_it != map1.end(); l_it++)
{
Node node=new Huffman(l_it->first,l_it->second);
pq.push(node);
}
}//得到Huffman树
void getTree()
{
while(pq.size()>1)
{
Node node1=pq.top(); //从优先队列中弹出最小的数
pq.pop();
Node node2=pq.top(); //弹出最小的数
pq.pop();
string key=node1->ch+node2->ch;
int value=node1->num+node2->num; //新结点的频数为两个叶子结点的频数和
Node node=new Huffman(key,value); //new新结点
node->lchild=node1; //左子树
node->rchild=node2; //右子树
pq.push(node); //将新结点加入优先队列中
//printf("%s %d\n",node.ch.c_str(),node.num);
}
}3、获取Huffman编码表
//获取Huffman编码表
void getMap(string code,Node node)
{
//当遍历结束时,返回
if(!node||node->ch=="")
{
return;
}
//当遇到叶子结点时,获取huffman编码并放入map2
if(node->ch.length()==1)
{
map2[node->ch]=code;
}
if(node->rchild)
{
//右结点+‘1’
Node right=node->rchild;
getMap(code+"1",right);
}
if(node->lchild)
{
//左结点+‘0’
Node left=node->lchild;
getMap(code+"0",left);
}
} 4、编码
void compress(const char* fin,const char* fout)
{
//以二进制形式打开输出文件,且如果文件已存在,则清空后再写入
ofstream file(fout,ios_base::trunc|ios_base::binary);
//判断文件是否正常打开
if(!file.good())
{
printf("Cannot open the file%s\n",fout );
return ;
}
//打开输入文件
ifstream in(fin);
//判断文件是否正常打开
if(!in.good())
{
printf("Cannot open the file%s\n",fin );
return ;
}
//迭代器,用于map的遍历
map::iterator l_it1;
//写入huffman编码个数
file<first.c_str()[0]=='\n'){
file<first.c_str()<second.c_str()<<" ";
}
char ch;
string s;
string cs="";
int length=cs.length();
string str="";
unsigned char byte;
unsigned long temp;
while(!in.eof())
{
// MAX 防止出现string长度超出限制。当文件很大时,必须要有此句
while(length=8)
{
//取前8b
str=cs.substr(0,8);
bitset<8> bits(str);
temp=bits.to_ulong();//转换为long类型
byte=temp;//转换为char类型
file< bits(str);
temp=bits.to_ulong();//转换为long类型
byte=temp;//转换为char类型
file< //将char转成string二进制串
string turnachar(unsigned char c)
{
string k="";
int j=128; //后八位为 1000_0000
for(int i=0; i <8; i++)
{
//判断原char该位数是0或1
k+=(unsigned char)(bool)(c&j)+'0';
j>>=1; //将1右移
}
//cout<译码篇
1、获取Huffman译码表
2、译码
//获取Huffman译码表并进行译码
void decompress(const char* fin,const char* fout)
{
//1、获取Huffman译码表
//以二进制的形式打开编码后的文件
ifstream in(fin,ios_base::binary);
//假如文件打开失败
if (in.fail()){
cout<<"Fail to open the file1 !!"<map4;
int size;
char key;
char h;
string value;
//如果只是>>这种的话,会读取不到\n,然后会出错
in>>size;
in.get(h); //读取掉空格
while(size>0)
{
in.get(key); //读取key
in>>value; //读取value
in.get(h); //读取掉空格
map4[value]=key; //将key与value写入map4
size--;
//cout<>"<0)
{
//开始解码
ss=sc.substr(0,i);
while(map4.find(ss)==map4.end()) //假如在Huffman表中找不到,继续读取下一位
{
i++;
length=sc.length();
//判断是否超过原字符串大小,避免报错
if(i>length){
check=true;
break;
}
ss=sc.substr(0,i);
}
//用于退出两层循环
if(check==true){
break;
}
//解码
result+=map4[ss];
//去除已解码的部分,继续解码
sc=sc.substr(i,sc.length()-i);
i=1;
}
//将解码后的结果写入文件
out< 解码也要用到turnachar()函数,在编码部分已给出。
最后
代码基本全了,不仅给出各个函数,全局变量也已给出,而主函数只是调用他们。
普通字符和中文都能适用,假如想进一步精进,可以使用图形化界面,真正弄成一个文本文件压缩的工具。