Python监督学习_神经网络（深度学习）

神经网络（深度学习）

深度学习算法往往经过精确调整，只适用于特定的应用场景。这里讨论简单的用于分类和回归的多层感知机(multilayer perceptron, MLP)，MLP也被称为前馈神经网络/神经网络。

1.神经网络模型

MLP可以被视为广义的线性模型。

display(mglearn.plots.plot_logistic_regression_graph())

 输入特征×系数 加权求和即输出，计算中间的隐单元（hidden unit），再加权求和。

display(mglearn.plots.plot_single_hidden_layer_graph())

这个模型需要更多的系数（权重）。为了让这玩意儿比线性模型更强大，在计算完每个隐单元的加权求和后，对结果再应用一个非线性函数----通常是校正非线性（rectifying nonlinearity，也叫校正线性单元或 relu）或正切双曲线（tangens hyperbolicus, tanh）。然后将这个函数的结果用于加权求和，计算输出结果。relu 截断小于0的值，而tanh 在输入值较小时接近-1，较大时接近1，用这两种模型给深度学习加buff。

line = np.linspace(-3, 3, 100)
plt.plot(line, np.tanh(line), label="tanh")
plt.plot(line, np.maximum(line, 0), label="relu")
plt.legend(loc="best")
plt.xlabel("x")
plt.ylabel("relu(x), tanh(x)")
plt.show()

 

权重都是要从数据中学习得到，需要我们设置的只有结点数，有的时候它可以小到10，有时可以大到10000.

mglearn.plots.plot_two_hidden_layer_graph()

2.神经网络调参

我们使用MLPClassifier

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
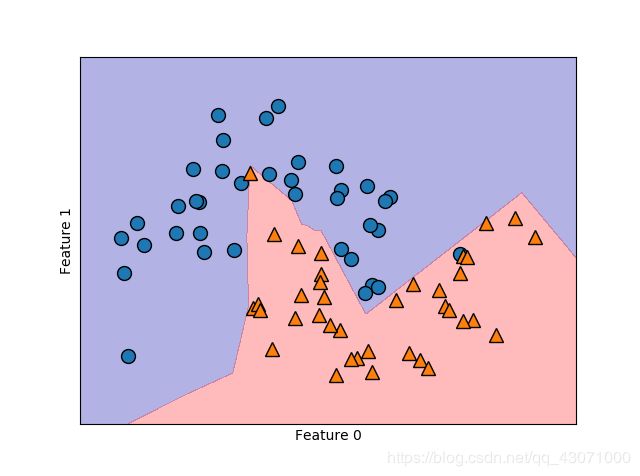
mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

 这个决策边界时非线性的，但是相对平滑，且用到了solver='lbfgs'。默认情况，使用100个隐结点，我们可以减少结点数量但仍然有个很好的结果。

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

 单元更少时，决策边缘参差不齐，默认的非线性是 relu。如果使用单隐层，那么决策函数将由10个直线段组成。

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
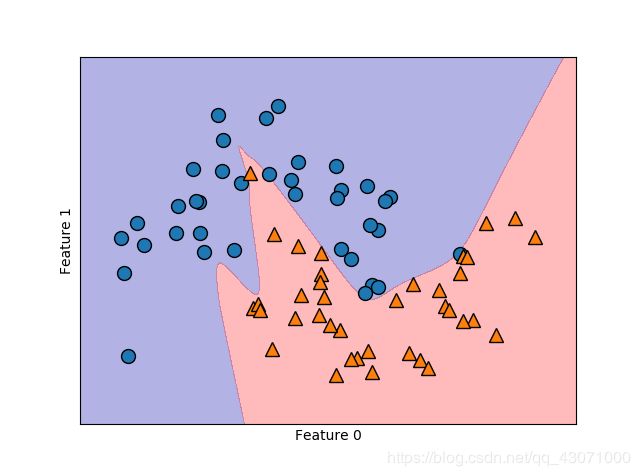
plt.show()

这次使用tanh非线性

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

 

 最后我们还可以使用L2惩罚使权重趋向于0，正如岭回归和线性分类器中所做的那样。MLPCassifier 中调节L2惩罚的参数是alpha (与线性回归模型相同)，默认值很小(弱正则化)。

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
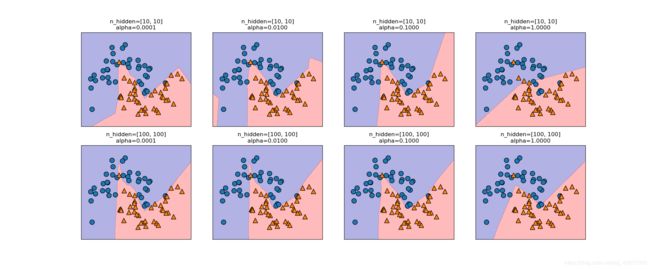
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for axx, n_hidden_nodes in zip(axes, [10, 100]):
    for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]):
        mlp = MLPClassifier(solver='lbfgs', random_state=0,
                            hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes], alpha=alpha)
        mlp.fit(X_train, y_train)
        mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
        mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
        ax.set_title("n_hidden=[{}, {}]\nalpha={:.4f}".format(
            n_hidden_nodes, n_hidden_nodes, alpha))
plt.show()

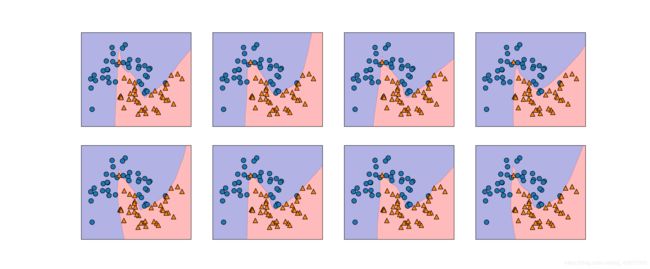
 控制神经网络的复杂度的方法有：隐层的个数、每个隐层中的单元个数与正则化。神经网络最开始权重是随机设置的，因此随机种子会影响它呢。

fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for i, ax in enumerate(axes.ravel()):
    mlp = MLPClassifier(solver='lbfgs', random_state=i, hidden_layer_sizes=[100, 100])
    mlp.fit(X_train, y_train)
    mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
    mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
plt.show()

 换个数据继续

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("Cancer cata per-feature maxima\n{}".format(cancer.data.max(axis=0)))

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
mlp = MLPClassifier(random_state=42)
mlp.fit(X_train, y_train)
print("Accuracy on training set: {:.2f}".format(mlp.score(X_train, y_train)))
print("Accuracy on test set: {:.2f}".format(mlp.score(X_test, y_test)))

MLP的精度相当好，但没有其他模型号，较之前的SVC相同，神经网络也要求所有输入特征的变化范围类似，最理想是均值为0，方差为1。这里人工完成，后期将用 StandardScaler 完成。

# 计算训练集中每个特征的平均值
mean_on_train = X_train.mean(axis=0)
# 计算训练集中每个特征的标准差
std_on_train = X_train.std(axis=0)
# 减去平均值，然后乘以标准差的倒数
# 运算后，mean=0, std=1
X_train_scaled = (X_train - mean_on_train) / std_on_train
X_test_scaled = (X_test - mean_on_train) / std_on_train
# 对测试集作相同的变换
mlp = MLPClassifier(random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

模型给出了超过迭代次数的警告，这是用于学习模型的 adam 算法的一部分，接下来增加迭代次数。

mlp = MLPClassifier(max_iter=1000, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

增加迭代次数提高了训练集的精度，但是我们需要泛化能力的提高，因此我们尝试降低模型复杂度，这里我们选择增加 alpha 参数（变化范围从0.0001到1），向权重添加更强的正则化。（注明，这个程序运行的是偶训练集的精度和书上不一致达到了1.000

mlp = MLPClassifier(max_iter=1000, alpha=1, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
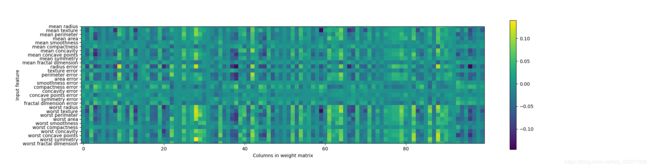
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

想要观察模型学到了什么，一种方法是查看模型的权重。行对用30个输入特征，列对应100个隐单元。

plt.figure(figsize=(20, 5))
plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')
plt.yticks(range(30), cancer.feature_names)
plt.xlabel("Columns in weight matrix")
plt.ylabel("Input feature")
plt.colorbar()

 我们可以推断，有些特征的重要性不是很大，有可能是隐单元的权重较小，也有可能是我们没有用神经网络可以使用的方式来表示它们。也可以将连接隐层和输出层可视化，但难以解释就算廖。虽然 MLPClassifier 和 MLPRegressor 为最常见的神经网络架构提供了易于使用的接口，但是他们只包含神经网络潜在的一部分。

最为完善的是基于 theano 库的 keras 、lasagna  和 tensor-flow ，这些库提供了更为灵活的接口，那些流行的深度学习库支持GPU。

3.优点、缺点和参数

主要优点是能够获取大量数据中包含的信息，并构建无比复杂的模型。缺点就是需要大量时间，最好数据均匀，对于不均匀的数据树的表现可能更好。调节神经模型和训练模型的方法有很多种。

估计神经网络的复杂度。最重要的参数层数和每层的隐单元的个数。在考虑神经模型复杂度的时，一个有用的度量是学到的权重的个数。神经网络通常的调参方法是首先创建一个大到足以过拟合的网络，确保网络可以对任务进行学习。之后，要么缩小网络，要么增大alpha来增强正则化，这可以提高泛化性能。

在我们的实验中，主要关注模型的定义：层数、每层的结点个数、正则化和非线性。对于如何学习模型和用来学习参数的算法，由参数 solver 决定，它有两个好用的选项，默认是 ‘adam’ ，大多数情况都很好，但对数据缩放很敏感。另一个是 ‘lbfgs’ ，其鲁棒性相当好，但在大型模型和大型数据集上的时间会比较长。还有更高级的选项 ‘sgd’ 。

fit() 会重置模型