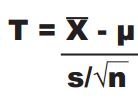概率论几大分布和统计学三大检测简述
二项分布
二项分布是一个离散概率分布
在n次独立的实验中, 事件A 发生的概率为p(不发生的概率则为1-p),那么最终事件A 发生k(k大于等于0,小于等于n)次的概率为:
nCk * p^k * (1-p)^(n-k)
其中 nCk 的意思是 组合(n中取k)
泊松分布
泊松分布是二项分布的一个变形和取极限,它通常被用来描述一段时间内或者一定空间内事件的发生次数的对应概率,用于小概率情况
给个连接: http://www.ruanyifeng.com/blog/2013/01/poisson_distribution.html
里面的例子举得很好。
与泊松分布相对的是指数分布, 指数分布对应的是两次事件之间间隔多久的概率,再进一步有一个gamma分布,它对应的是n次事件之间的间隔时间。gamma 分布可以这样理解: 一段时间内发生了k次变化(伯努利事件), 每次变化都是相同的,结果记为正, 那么最终这段时间过后事件的结果为正, 那么对k取0到正无穷的积分,就能得到gamma分布了.
正态分布
正态分布是一个连续概率分布, 在已知均值和方差的情况下,有如下分布:
其中μ是均值(数学期望),σ是标准差,它的平方就是方差。它的函数图是钟形曲线。
这个分布在自然界中很常见下面要讲的3个统计学分布都跟正态分布有联系。
值得一提的是,正态分布在多维概率的情况下,有很多有意思的属性,比如 一个多维正态分布的边缘函数必是一维正态分布,若干个一维正态分布的代数和构成的分布还是正太分布(再生性),多维正态分布的条件概率分布也是正态分布。总之正态分布很牛逼。
判断一个分布是否是正态分布有好几种办法:通过偏度S是否为0,峰度K是否等于3。还有比较正式的JB检测。
卡方分布、检测
卡方分布是从正态分布中衍生出的一种分布。其定义是若干个随机变量的平方和也服从一种分布,即卡方分布。
卡方检测可以从《深入浅出统计学》一书第14章中找到一个非常形象的例子——对一个赌博机进行1000次操作,各种结果的抽样次数与其期望值的差即是一个个服从正态分布的独立变量(天文学中测量误差研究正是正态分布的起源之一。书中的公式还要把差值除以期望值,这是为了归一化),差值的平方和服从卡方分布。对数据进行5%的假设检测,查卡方分布表就可以得出结论。
卡方分布还有一个自由度的概念,它指自由变量的个数。
注意卡方分布不是用来检测正态分布的,而是检测这些随机变量是否服从其给定的概率的。
t检测
t检测应用于小样本的情况。中心极限定理告诉我们随着样本的容量变大,样本的均值将成正态分布,而当样本较小的时候分布则更接近t分布。在计算正态分布的置信区间时,我们通常把正态分布转化成标准的正态分布N(0,1),在t分布中我们也有一个类似的公式(学生定理):
其中S是样本的标准差,μ是总体的均值,计算出的值T服从n-1的t分布。
t分布其实是由正态分布和卡方分布共同推导而来的,它的思路是样本的均值服从正态分布,而实际方差不能仅仅简单等同于样本中计算来的方差,要等同于一个服从卡方分布的方差,最后推导出了t分布。t分布中也有自由度的概念,往往取样本数减去1为自由度v。
t检测分为单样本和双样本两种情况, 单样本给定一个样本和一个总体的均值, 判断这个样本是不是来自这个总体.双样本判断两个样本是不是来自同一个总体.
t分布和t检测的用途很广, 还可以参考我的这篇文章:http://blog.csdn.net/rav009/article/details/44457913
F检测
在线性回归中,要求因变量有一个齐方差性,即因变量的方差不能随着自变量的改变而改变,可以用F检测来检验齐方差性。
F检测就是从方差的角度来判断两组样本是否来自同一个总体。其概率密度函数pdf实际是两个不同自由度的卡方分布的pdf的商。F检测的表中值就是两个样本中的大的方差除以小的方差。如果得到的样本大于表中的值,那么就拒绝两个样本来自同一个方差的假定。