轮式移动机器人的运动控制入门

目的

　　轮式移动机器人（主要针对汽车）的镇定和跟踪控制理论和方法入门。

　　　　　　　

1　前言

　　如果你常看历史剧可能会发现一个有意思的现象，古代的车几乎都是两轮形式的。不管是东方还是西方，超过两轮的车很少见到。这是为什么呢？究其原因当然有很多，但最主要的可能是古人一直没弄明白多车轮（三轮以上）的车怎么拐弯。可别小看这个问题，车辆转弯不是那么容易的，每个车轮的速度、角度必须满足一定的运动关系。车轮的发明是个重大突破，怎么把多个车轮组合起来用好也是个挑战，本文简单探讨一下其中的难点和方法。

　　和大多数的控制系统一样，移动机器人的控制任务也可以简单分成以下两种：
　　1　镇定：控制机器人到达并稳定在某个静止的状态，实际生活中的例子就是把汽车停到一个指定的停车位里。
　　2　跟踪：控制机器人跟踪某个运动着的状态（即轨迹），实际生活中的例子就是让汽车沿着车道中心线行驶。
　　$★$　这两个任务哪个更难呢？
　　我们都知道，对于机械臂来说，控制它稳定到某个状态比控制它跟踪一个空间轨迹更简单，所以很多人理所当然地认为轮式移动机器人的“镇定”比“跟踪”更简单。但是实际情况是镇定更难，这是由于运动约束的存在${}^{[1]}$。也就是说轮式移动机器人和机械臂的控制难度刚好反过来了。哈哈！有意思吧。

2　汽车模型

　　一般的汽车都是四轮形式，为了实现顺畅地转向，前轮采用艾克曼转向机构，后轮采用差速器。在大多数论文中，一般把四轮汽车用两轮的自行车模型描述，这样的简化不改变问题的本质，而且处理更方便。这样得到的模型可以用式$(1)$所示的方程来描述，称为运动学方程。本文只考虑运动学模型的控制，不考虑动力学。因为控制上的难度主要是运动学造成的。
$$\begin{array}{rl}& \dot{x}=vcos(\theta )\\ & \dot{y}=vsin(\theta )\\ & \dot{\theta }=\frac{v}{L}tan(\varphi )\end{array}\text{\hspace{1em}(1)}$$

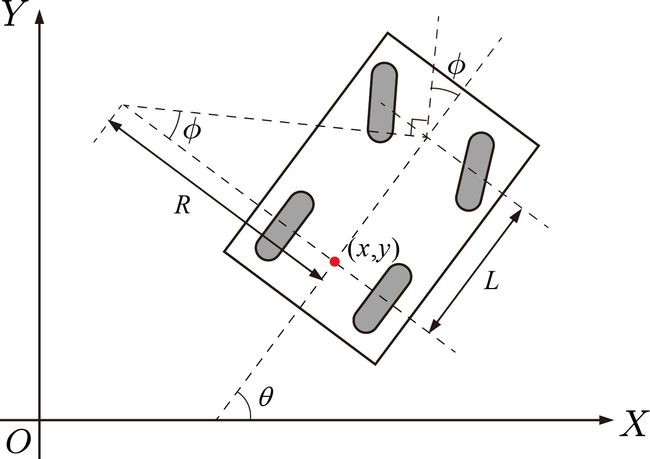
　　其中，$(x,y,\theta )$是车后轴中心点的位置和汽车的姿态，可以称为状态量（常被称为位姿），是我们想改变的；而$(\varphi ,v)$是控制量，是我们能直接改变的，如下图所示。$\varphi$代表自行车前轮的转角（单位是度或者弧度），$v$代表后轮的速度（单位是m/s）。控制量一般总是受约束的，例如$-30°\le \varphi \le 30°$，$-1$m/s$\le v\le$ $1$m/s。转向角度$\varphi$有个上下限，这导致机器人也有个最小转向半径$R\le R_{min}=L/tan({\varphi }_{max})$，其中$L$是前后车轮轴的距离。这一特点是自行车模型与其它机器人模型的重要区别。有一种两轮形式的机器人模型叫差速机器人，它是最常见也是被研究最多的机器人了。差速机器人没有转向半径的限制，可以原地转向，所以它的控制比自行车模型容易，这也是为什么你们家的扫地机器人采用这种形式的原因。
　　简单来说，移动机器人的控制任务就是通过改变$(\varphi ,v)$来改变$(x,y,\theta )$达到期望的状态，这个看起来简单的模型和任务其实一点也不简单，为了研究它不得不动用一些数学中的重武器。

　　在讨论控制问题之前，我们先分析一下这个模型有什么特点：
　　1　从数学的角度看，方程中包含状态$\theta$的三角函数，所以它是个非线性系统。这是个坏消息，因为非线性系统的分析和控制一般比线性系统更困难。
　　2　从驱动数量的角度看，模型中控制量的个数少于状态量的个数（$2<3$），因此它是个欠驱动系统（underactuated），这意味着我们要用少数控制量去影响干预多数状态量。
　　3　从运动或者约束的角度看，这个模型还包含非完整约束，什么是非完整约束呢？我们给方程组$(1)$中的第一个等式两边乘以$sin(\theta )$，给第二个等式两边乘以$cos(\theta )$，然后将两式相减就会得到式$(2)$，这个式子表示的就是一个非完整约束。区分“完整约束”和“非完整约束”的标准就是能不能积分，如果能将状态的导数项积分得到代数方程，那就是完整约束。例如$x_1{\dot{x}}_1+x_2{\dot{x}}_2=0$可以积分成$\frac{1}{2}{x}_1^2+\frac{1}{2}{x}_2^2=c$，$c$是个与初始条件有关的常数。再看式$(2)$则不能积分。对于完整约束，由于可以积分得到代数方程（速度约束变成了位置约束，阶数降低），因此可以通过变量替换消去一些状态变量（例如用$x_1$表示$x_2$从而消去$x_2$），让问题变得更简单。但是对于非完整约束就不行了。非完整约束系统总是欠驱动系统。飞机、汽车、船舶都是非完整约束系统，具有类似的性质，知道汽车怎么控制就能推广到飞机轮船。
$$\begin{array}{rl}& sin(\theta )\dot{x}-cos(\theta )\dot{y}=0\end{array}\text{\hspace{1em}(2)}$$

　　4　它还是个无漂移系统（Driftless），这里的“漂移”跟赛车没关系。无漂移的意思是当控制量都为零时，状态量不会改变（即导数项也为零）。不给控制输入系统就静止不动相当于没有惯性，这个很容易检验。
　　5　这个模型是一组常微分方程，如果控制量只依赖状态不依赖时间，那么它还是个自治系统（Autonomous system）。自治系统是针对闭环系统的。
　　6　从输入控制量的角度看，经过简单的替换（令$\gamma =\frac{v}{L}tan(\varphi )$），它还可以变成仿射非线性系统（Control-affine systems），即模型虽然关于状态量仍然是非线性的，但是关于控制量$(v,\gamma )$却是线性的。
　　7　它也是个微分平坦（differentially flat）系统，控制量可以用状态量及其导数来表示，如式$(3)$。其中，$\sigma =sign(⟨(\dot{x},\dot{y}),(cos(\theta ),sin(\theta ))⟩)$表示运动方向。
$$\begin{array}{rl}& v=\sigma \sqrt{{\dot{x}}^2+{\dot{y}}^2}\\ & \varphi =arctan(L\dot{\theta }/v)\end{array}\text{\hspace{1em}(3)}$$

3　可控性

　　了解完模型的特性，我们下面最关心的是它的可控性。可控就是能通过施加控制使系统到达状态空间中的任意一个状态，反之就是不可控。可控性自然是很重要的，因为如果一个系统是不可控的，也就意味着不管你施加怎样的控制量都到不了想要的状态，那我们就不再费劲去寻找一个控制律了。注意可控性研究的是模型本身的性质，与控制量无关，它不关心控制量是多大。
　　$★$　那么模型$(1)$是不是可控的呢？
　　我们最熟悉、也最简单的是线性系统，翻出你大学的《自动控制原理》课本，可以找到线性系统可控性的充要条件是可控性矩阵是满秩的。但是很遗憾，我们面对的模型$(1)$是个非线性系统，得寻找更一般的方法。根据Chow的定理${}^{[1]}$，模型$(1)$是可控的。这个结论是符合我们的直觉的，汽车总是能到达任意一个位姿，虽然过程可能稍微有点麻烦（开过车的都有体会），否则汽车就得重新设计了。

　　　　　

　　可控性回答的是“能不能”的问题，可是它没有回答“怎么做”，更没回答这样的控制应该有什么样的限制。显然我们是不满足止步于此的，我们还要追问。
　　我们可以设计一个开环的控制（不依赖状态）到达给定的状态吗？即使可以，实际系统总会有各种误差和扰动。可能理论计算的很好，实际一使用时会出现偏差，所以最好找一个闭环的反馈控制$u$，也就是依赖状态的控制，记成$u=u(x)$（这里滥用一下符号，用$x$表示机器人的状态）。如果还有什么要求的话，我们希望这个控制最好是状态的光滑函数（$u(x)\in C^{\infty }$），满足这个性质算是比较基本的要求，毕竟常见的初等函数都是光滑的嘛，方便我们分析构造。那么这样的要求算不算太高呢？
　　$★$　模型$(1)$是否存在光滑的反馈控制呢？
　　一个叫Brockett的哥们第一个回答了这个问题：不存在。Brockett在论文《Asymptotic stability and feedback stabilization》中给出了系统存在光滑的反馈控制的必要条件，这就是大名鼎鼎的Brockett定理。很遗憾，我们的机器人模型不满足这个条件。论文使用了微分几何和Lyapunov稳定性理论等工具。我看这个结论很少被提到，只有贾欣乐解释过，所以下面我翻译一下论文的基本思想。

Brockett

　　Brockett定理的证明
　　Brockett考虑的是最一般的自治非线性系统：
$$\begin{array}{r}\dot{x}=f(x,u)\end{array}\text{\hspace{1em}(4)}$$　　假设这个系统的平衡点是$x_0$。啥是平衡点？平衡点就是速度（即状态的导数）等于零的点（$\dot{x}=0$），速度为零意味着系统到达这个点就不动了，也就是到达平衡状态了，顾名思义。平衡点不一定是稳定点。一般我们把想到达的目标状态设为平衡点。当然，都到目标状态了，控制量也就等于零了：$f(x_0,0)=0$。
　　然后作者描述了这篇论文要解决的唯一的一个问题：能不能找到一个光滑的函数$u(x)$使系统$(4)$在平衡点$x_0$处渐进稳定。注意$u(x)$的写法表示控制量$u$只依赖于状态$x$，不依赖其它的东西，比如不依赖时间。所以即使你找不到一个光滑$u(x)$，那不意味着你找不到一个光滑的$u(x,t)$，很多后来的学者就是这么干的，把时间引进来，或者牺牲光滑性，找一个不连续的解。
　　论文第二部分，Brockett开始给出一些基本定义，但是是用微分几何的语言描述的。对于没学过微分几何的同学，看到这里估计腿一软就给跪下了。无奈笔者也不太懂。不过即使这部分看不懂好像也不太妨碍理解后面的证明部分。当然能掌握微分几何是最好的，因为好多论文都使用了微分几何的工具和术语，如果不懂看起来论文来会很吃力。懂微分几何的另一个好处是让你的论文更上档次，毕竟相当多从事机器人研究的学者数学都停留在初等微积分和线性代数的水平。
　　有一个可微的流形$X$（对于咱们来说，$X$就是移动机器人的所有位姿$(x,y,\theta )$组成的构型空间，所以$X={\mathbb{R}}^2\times S$）。在$X$上再定义一个向量丛$\pi :E\to X$。这里解释一下向量丛，它是纤维丛的一个特例，也就是纤维是向量空间的纤维丛。最常见的向量丛就是切丛。好吧，这下又得解释纤维丛。直观的理解纤维丛，可以把它想象成一把刷子。其中，$E$是整个向量丛空间（被称为总空间，整个刷子），而$X$是$E$的基础（所以又叫基空间，刷子的柄），刷子毛就是纤维。纤维丛是微分几何中一个比较重要的概念，虽然比较抽象，但是如果了解了来龙去脉还是不难理解的。假如我们只考虑欧式空间，完全不需要使用这些匪夷所思的东西，生活简单又惬意。但是真实世界很多空间是非欧的，这就像几千年来人们一直认为地球是平的，突然有人发现地球是圆的，那原来的一些数学原理就得改造了，包括纤维丛、共变导数等等很多抽象的东西都是为了改造而出现的。
　　$\mathrm{T}\mathrm{X}$是$X$上的切丛，切丛就是把$X$上所有点（$\forall x\in X$）处的切空间（$\mathrm{T}{}_x\mathrm{X}$）合起来看成一个整体，这样构成的空间。每个点$x$处的切空间就是切向量——也就是速度向量$(\dot{x},\dot{y},\dot{\theta })$组成的线性空间。${\pi }^{\ast }\mathrm{T}\mathrm{X}$是$\mathrm{T}\mathrm{X}$的拉回（pullback）。这句我也看不太懂，猜测是：${\pi }^{\ast }\mathrm{T}\mathrm{X}$是$\mathrm{T}\mathrm{X}\to \mathrm{E}$。${\pi }^{\ast }\mathrm{T}\mathrm{X}$的一个截面（section）就是给$E$中的每个点分配一个$\mathrm{T}\mathrm{X}$空间中的速度向量。截面是纤维丛里的一个重要概念，这里它就是映射：${\pi }^{\ast }\mathrm{T}\mathrm{X}\to \mathrm{E}$。如果给$E$选个平凡的局部坐标系，那么这个截面就表示为$\dot{x}=f(x,u)$，称这样的截面为一个控制系统。费了半天劲才刚给出了控制系统的正式定义。

　　论文第三部分就开始证明了，在正式证明之前，Brockett先举了一个众所周知的例子，就是线性系统 $\dot{x}=Ax+Bu$ 可控的充要条件。然后，对于非线性系统，存在连续可微控制律的必要条件有三个：
　　(1)　非线性控制系统线性化后不存在不可控的模式，即不存在实部为正的特征值；
　　(2)　平衡点$x_0$附近存在一个邻域N，使得对于N中每个点$\xi$总存在一个控制$u_{\xi }$能够将控制系统$\dot{x}=f(x,u_{\xi })$转移到平衡点$x_0$；
　　(3)　映射$\gamma :(x,u)\to f(x,u)$能够覆盖一个包含原点0的开集；
　　最重要的是条件(3)，Brockett是这样证明的：
　　如果$x_0$是控制系统$\dot{x}=a(x)$的渐进稳定平衡点，那么一定存在一个Lyapunov函数$V$满足这样的性质：
　　●　$V(x)>0$（对于所有的$x\ne x_0$都成立）
　　●　$V$是连续可微函数
　　●　$V$的水平集$V^{-1}$就是一系列的同伦球。
　　为了直观的展示Lyapunov函数和它的水平集，先看一个简单的例子。假设Lyapunov函数是这样的：$V(x,y)=(x^2+y^2)/2$，就是个抛物面，它的图像如下图所示。$V$的水平集就是$V$等于常数的点组成的集合：$\{(x,y)|V(x,y)=c\}$，也就是用水平面截抛物面得到的一个个圆圈，就是图中的红圈（只画了有限的几个）。这个Lyapunov函数是二维的$V(x,y)$。对于三维的Lyapunov函数$V(x,y,z)=(x^2+y^2+z^2)/2$，它的水平集就是个球了，再高维度的都统一叫球。

　　存在$\alpha$和$ϵ>0$使得在$V^{-1}(\alpha )$上，内积$⟨\partial V/\partial x,a(x)⟩<-ϵ$。这意味着对于足够小的$\Vert \xi \Vert$，向量场$\dot{x}=a(x)+\xi$仍然指向同伦球$V^{-1}(\alpha )$的里面。通过求解$\dot{x}=a(x)+\xi$可以得到一个到自身的连续映射$\{x|V(x)\le \alpha \}$。根据莱夫谢茨不动点定理，这个映射具有一个不动点，这个不动点一定是$\dot{x}=a(x)+\xi$的平衡点。这意味着我们可以求解$a(x)=\xi$，不管$\Vert \xi \Vert$多小。如果$a(x)=f(x,u(x))$，那么必然有代数方程$\xi =f(x,u(x))$可解。到此就完成了证明。
　　对于我们关心的汽车模型$(1)$，可以用上面的证明结论检验一下它为什么不存在光滑的反馈控制律。考虑速度$\xi =(0,c,0)$的例子，这里$c$是个不为零的常数。当状态$(x,y,\theta )$中的角度$\theta =0$时就不存在解。直观的讲就是，汽车不能有相对车身侧方向的速度，这是符合我们的直觉的。
　　证明用到了莱夫谢茨不动点定理。这个定理更难理解，不再展开。不过这个人倒是值得一提，数学家莱夫谢茨（Lefschetz）年轻时因为事故失去双手，后来身残志坚钻研数学，照片中戴手套的为假手。

莱夫谢茨 (Lefschetz)

　　因为Brockett的结论，人们放弃了寻找连续反馈控制律的尝试，转而寻找不连续或者时变的控制。

4　几种镇定控制律

　　这一节我们的目的是检验几种前人提出的镇定控制律的控制效果。
　　1　首先我们试试这本书《Robotics, Vision and Control》中第4.2.4节使用的一种简单控制律，它与论文$[3]$中提出的差不多。它的思路是首先将模型$(1)$从直角坐标系转换到极坐标系，然后再在极坐标系中设计一个比例控制：
$$\begin{array}{rl}& v=k_{\rho }\rho \\ & \gamma =k_{\alpha }\alpha +k_{\beta }\beta \end{array}\text{\hspace{1em}(4)}$$

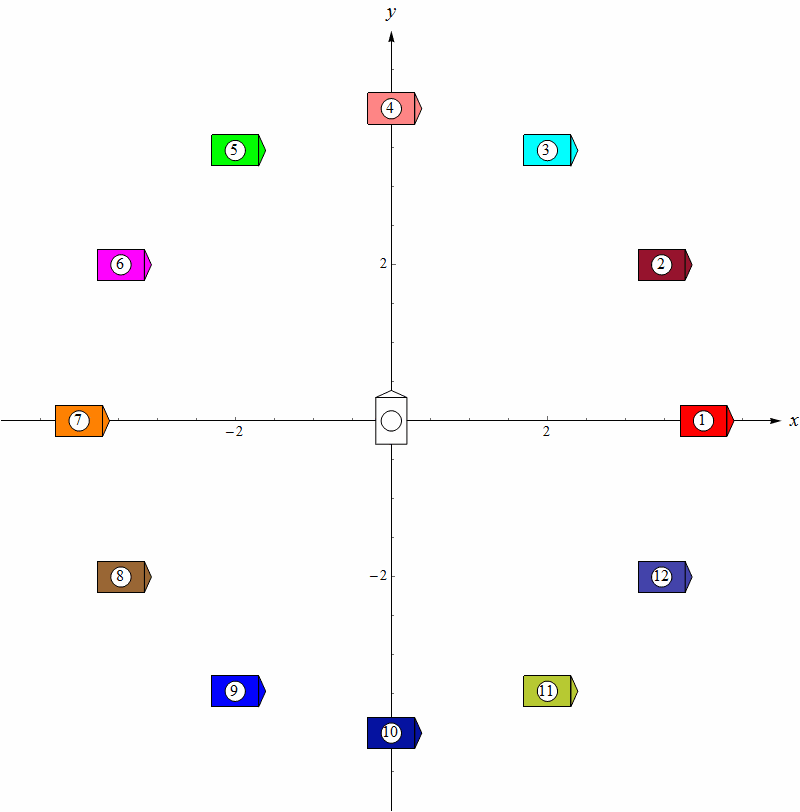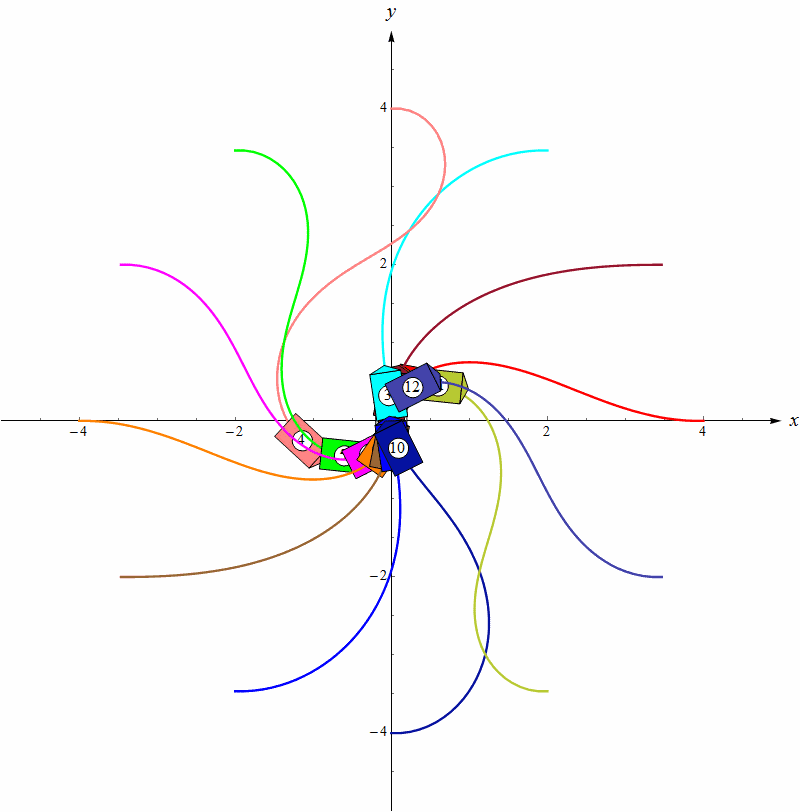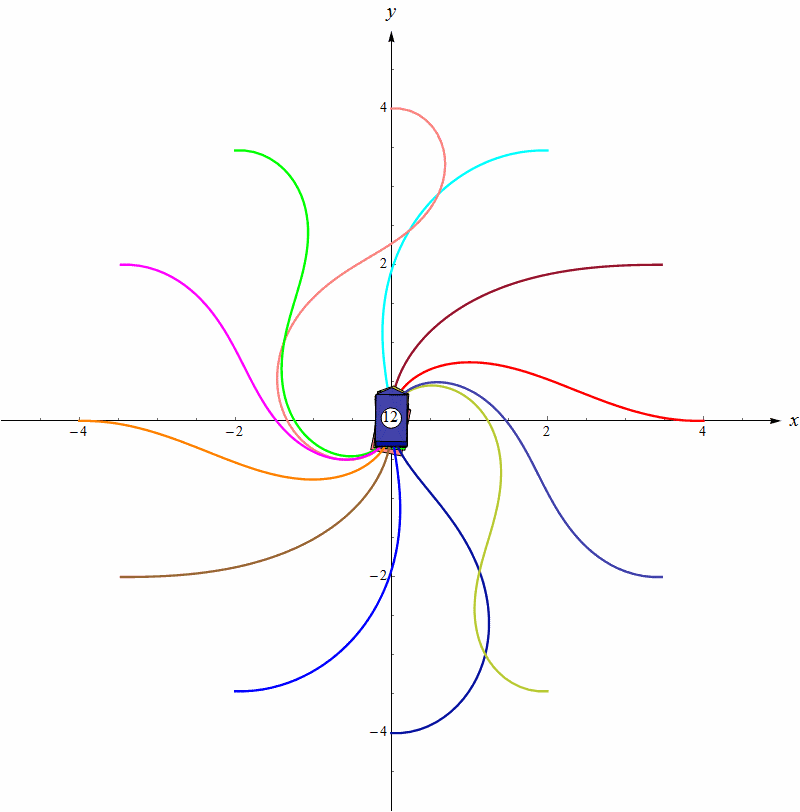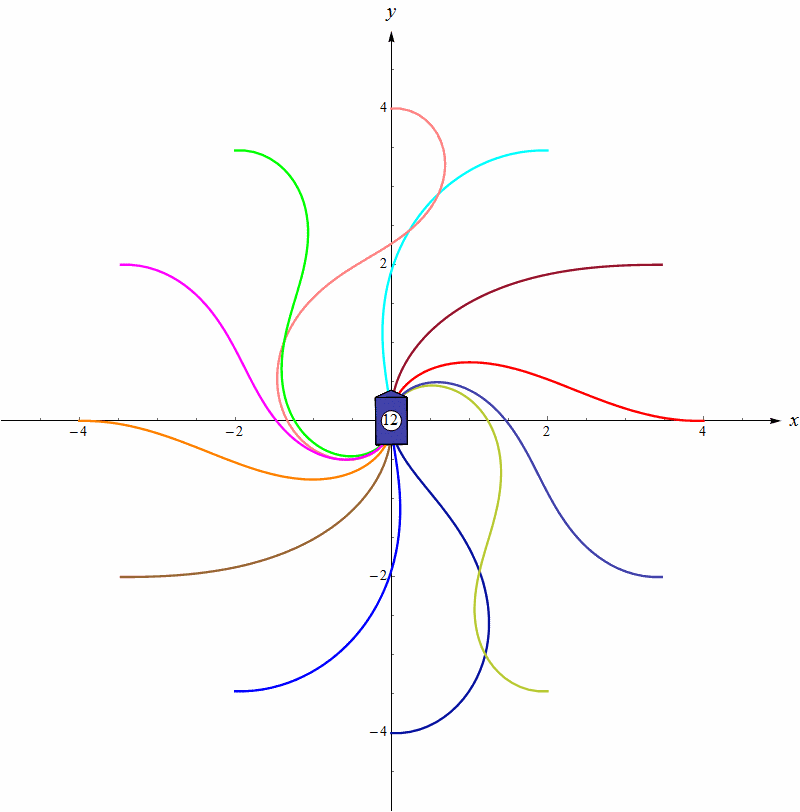
　　等等，前面不是证明了不存在光滑反馈控制律吗？这个控制律在$\rho =0$处不连续，所以不违背Brockett定理。仿真的效果如下图，我们把目标位置设在原点处，目标姿态是90°，（多个）机器人的初始位置处于一个圆周上，初始角度都是0°。左图是没有最小转向半径约束的情况，右图是加上最小转向半径约束的情况。可见这个算法不能处理控制量受约束的模型。这不奇怪，因为原文只是针对差速机器人模型提出来的。

　

　　2　有学者提出了不连续的反馈控制，。

　　3　有学者另辟蹊径，把时间引入了控制量，提出了时变的反馈控制，例如论文$[4]$。

　　4　还有学者考虑了几种特殊情况下的反馈控制。

参考文献

[1]　Feedback Control of a Nonholonomic Car-like Robot, 第7页.
[2]　A Mathematical Introduction to Robotic Manipulation, 第329页.
[3]　Closed loop steering of unicycle like vehicles via Lyapunov techniques, M. Aicardi, IEEE Robotics & Automation Magazine, 1995.
[4]　Time-varying Feedback Stabilization of Car-like Wheeled Mobile Robots, Claude Samson,
The International Journal of Robotics Research.