浅谈MergeSort

基本数据结构算法实现——浅谈归并排序(nlogn)

本篇文章基于左神对于归并排序的思想推导以及本人对于归并排序的理解。
归并排序，顾名思义，其核心在于将一个无序数组通过不断地拆分-有序的递归过程(Process)将一个整体的数组被分解成以数组中单一元素为基本单位的多区域集合，其中每个单一区域中的元素数量为1，此时，在每个单一区域中设置两个引用(左引用l与右引用r)，利用两个引用，使得每个单一数组中的元素变为有序。最后执行merge方法(融合)，使得左右两边有序的两个单一区域进行合并，合并的过程是简单的递推过程。

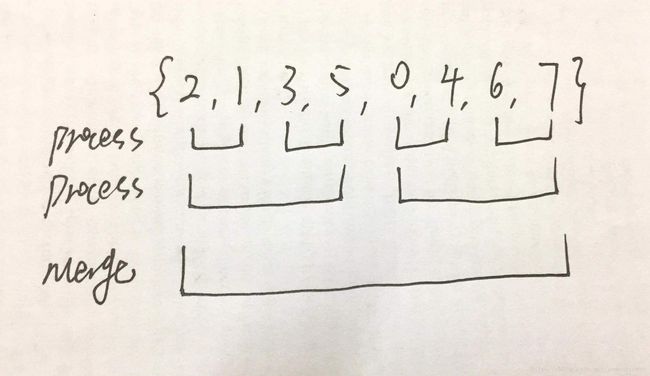
MergeSort—Process递归过程

本文使用测试用例{1,3,4,2,5}进行举例。首先，我们先看Process过程：

Process过程如上图所示，对于数组{1,3,4,2,5}进行归并排序的Process过程如图所示，其中，在数组中设置了左引用(l)与右引用(r)，首先找到数组的中点(中间元素)，M的取值我选择了位运算，因为如果使用传统的(L+R)/2，在某些情况下会造成数组溢出的后果，而对于整型数组而言，可以采用移位方法进行中间元素的获取，即M=L+(R-L)>>1(数值的二进制位右移一位等于改数除以2)。在设置了l，r，m(如图所示)之后，开始我们的Process递归过程，数组被分为左右两个区域，其中，左区域的左边界为l，右边界为m；右区域的左边界为(m+1)，右边界为r。再将左右两区域进行Process，以此类推，直到得到单一元素区域。在递归完成之后，数组的拆分-有序部分就结束了，接下来进行归并排序的核心处理过程，Merge(在后面部分进行讲解)。
Process过程的代码如下：

代码块—Process过程

//数组的(拆分->有序)部分
public int[] MergeSort(int[] arr){
    if(arr==null || arr.length<2){
        return;
    }
    Process(arr,0,arr.length-1);
}

public static void Process(int arr,int l,int r){
    if(l==r){
        return;
    }
    int m=l+((r-l)>>1);//这里采用移位的方法处理数值减半的操作，以防止数组(l+r)造成的数组越界现象
    Process(arr,l,m);//数组的左半区域O(N/2)
    Process(arr,m+1,r);//数组的右半区域O(N/2)
    Merge(arr,0,m,r);//merge方法O(N)是归并排序的核心部分，将在下面部分介绍
}   

MergeSort—Merge过程

Process过程结束后，数组的左半区域及右半区域已经有序，接下来是我对Merge过程的剖析：

MergeSort的Merge过程如上图所示，谈到Merge，这里有一个很蠢的做法，继续合并两个左右区域数组，小的数就放左面，大的数放在右边，为什么说它很蠢呢，在最坏情况下，如果左右两区域的元素进行两两比较进行交换，那么可想而知，时间复杂度将会很高，所以，这就体现优化的Merge方法的作用了，在左右区域各设置一个引用p1与p2，p1位于l位置，而p2位于(m+1)位置，这里设置一个help数组，用于获取比较得到的较小的数。
在Merge开始的时候，由于左右区域已经有序，因此可以分别从两区域的左侧开始进行比较，首先比较arr[p1]与arr[p2]的值，谁小就获取谁然后将其放入help数组 ，然后较小的元素下标右移一位，再次进行arr[p1]与arr[p2]的比较，如果遇到arr[p1]==arr[p2]的情况，那么获取arr[p2]的值，然后p2右移一位(因为最终数组的左区域是一定要小于右区域的，前提是要求升序排序数组，反之则获取arr[p1]的值即可)，那么，问题来了，什么时候跳出比较？两区域一直不断遍历下去，指针也一直在右移，也就是说，当跳出比较的时候，一定存在一个区域的指针越界了(p1超过了m或者p2超过了r)，so，接下来把还未遍历完全的区域的元素依次放入help数组中即可，直到p1,p2全部越界，此时help数组中的元素已经完全有序，再把数组中的元素全部放回至arr中即可，至此，Merge完成，MergeSort算法排序完成。
Merge过程的代码如下：

代码块—Merge过程

    public static void merge(int[] arr, int left, int mid, int right) {
        int[] help = new int[right - left + 1];//令辅助数组的长度等于原数组
        int p1= left;
        int p2= mid + 1;
        int i = 0;
        while(p1<=m && p2<=r){
        //下面这行代码，同时做了3件事
        //1.获取较小元素并放入help数组
        //2.help角标向右推进
        //3.左右区域指针向右推进
            help[i++]=arr[p1]//下面两个while循环，只能满足一个，另一个无论如何都不会满足
        while(p1<=m){
            help[i++]=arr[p1++];
        }
        while(p2<=r){
            help[i++]=arr[p2++];
        }
        //help的左边界是l，因此arr获取元素的时候，要从l边界开始，而不是0，这个地方容易出错
        for(int j=0;j

至此，MergeSort算法的全部过程的剖析+代码解析已全部完成，接下来我们看看它的时间复杂度，归并排序究竟好在哪里？

优化了Merge的MergeSort时间复杂度

Merge方法的好处在于省略了元素两两遍历+比较的过程，将之转为两区域指针不断推进从而获取较小元素的递推过程，从而节省了算法的时间复杂度。现在，回去看看Process过程中的部分核心代码：

对于左半区域的Process过程，遍历了N/2，同理，右半区域遍历了剩下的N/2，而Merge方法的左右区域的比较过程，整体比较了N次，因此可得到其整体时间为T(N)=2*T(N/2)+o(N)，我们将公式分解最终得到MergeSort的时间复杂度为O(nlogn)。
下面让我们来看看归并排序在数组问题中的应用，来看看经典的数组小和问题是怎么通过归并排序解决的。

小和问题—归并排序的实现

题目描述：在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和，求一个数组的小和。
例子：
[1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16。
看完这道题的题目，我刚开始想到的是一个很蠢的点子，遍历数组，随着区域的扩张，比较区域最右边的数和其他的数再将比最右边的数小的数累加到res里就行了，但是这么做，时间复杂度是非常高的，如果是面试的时候这么做，那么面试官很有可能在你做一半的时候就睡着了。
这道经典的数组题目完美诠释了MergeSort的应用，利用Merge方法，通过比较左右区域的元素值，即可得到最终的小和，因为该题比较经典，过多的描述就不多说了，直接看代码：

代码块—小和问题

    public static int smallSum(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;                                  
        }
        return mergeSort(arr, 0, arr.length - 1);
    }
    //arr[l...r]范围上，在排序的过程中，求出所有的小和，并返回
    public static int mergeSort(int[] arr, int l, int r) {
        if (l == r) {
            return 0;
        }
        int mid = l + ((r - l) >> 1);//mid=(r+l)/2,防止l+r溢出
        //一个数除以2相当于这个数的二进制表示右移一位
        return mergeSort(arr, l, mid) + mergeSort(arr, mid + 1, r) + merge(arr, l, mid, r);
    }

    public static int merge(int[] arr, int l, int m, int r) {
        int[] help = new int[r - l + 1];
        int i = 0;
        int p1 = l;
        int p2 = m + 1;
        int res = 0;
        while (p1 <= m && p2 <= r) {
            res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }
        while (p1 <= m){
            help[i++] = arr[p1++];
        }
        while (p2 <= r) {
            help[i++] = arr[p2++];
        }
        for (i = 0; i < help.length; i++) {
            arr[l + i] = help[i];
        }
        return res;
    }

代码的核心在与归并排序的过程中，不断的获取小和，最终返回一个完全有序的数组以及数组的小和，具体的代码讲解与Process过程、Merge过程极为类似，只是在Merge过程中，添加了累加数res来获取比较得到的较小元素。
至此，归并排序的介绍，剖析与应用已全部完事，作者是一名刚步入初级算法学习的小白，还在慢慢磨炼(煎熬)的过程中。

目录

---