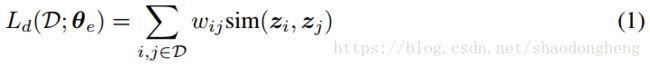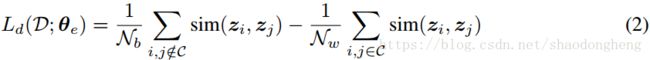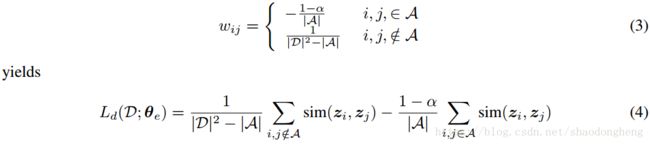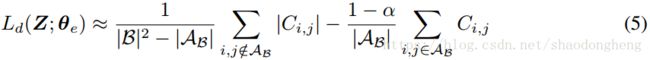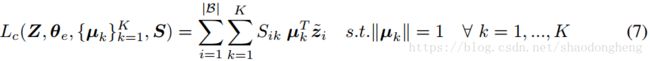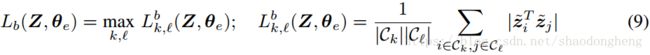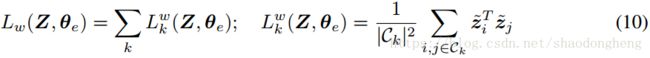Deep Discriminative Latent Space for Clustering 翻译

Deep Discriminative Latent Space for Clustering 翻译

摘要：

聚类是数据分析和机器学习中最基本的任务之一。它是许多数据驱动应用程序的核心，旨在将数据分成具有相似模式的组。此外，聚类是一个复杂的过程，受到数据表示方法选择的显著影响。最近的研究通过有效地学习这些表示来证明了令人鼓舞的聚类结果。在大多数这些工作中，深度自动编码器最初被预先训练以最小化重建损失，然后与聚类质心联合优化以便改进聚类目标。这些工作主要集中在程序的聚类阶段，而不是利用初始阶段的潜在益处。在本文中，我们建议在自动编码器预训练阶段期间针对判别的成对损失函数优化自动编码器。我们证明了所提出的方法所获得的高精度以及它的快速收敛性（例如，在预训练阶段，在不到50个时期内，在MNIST上达到92％以上的准确度），即使是小型网络也是如此。

1 引言

传统上，大多数学习方法一直在分别处理表示 - 学习/特征选择和聚类。然而，最近的研究发现，学习最佳表示的聚类优于传统方法。在大多数这些工作中，首先训练深度自动编码器以减少重建损失。接下来，联合优化编码器参数和聚类参数（例如，K均值质心），以便提高整体聚类精度。然而，我们观察到，在大多数情况下，聚类阶段相对于预训练阶段的改善不超过15％-20％的准确度。因此，在预训练阶段达到高精度是至关重要的。此外，由于重建和聚类之间的自然权衡，重建损失不是聚类的最佳选择。重建旨在重现原始数据中的每个细节，而聚类旨在将所有可能的变化减少到几个模板中。

在本文中，我们提出了一种新的统一框架，用于学习面向聚类的表示。我们建议在预训练阶段优化自动编码器，关于判别损失函数，其鼓励面向聚类的表示。判别损失是批次中数据点之间所有成对相似性的加权和。最小化这种损失意味着使数据点的表示尽可能不同。在平衡数据集的假设下，大多数数据对确实不相似，并且它们中只有一小部分是相似的（即，仅在簇对内）。因此，利用这种损失是合理的。所提出的优化方案能够利用可以快速训练的相对小的网络。对于聚类阶段，我们提出了一种联合优化方案，该方案在优化聚类目标的同时保持成对判别丢失。我们将所提出的算法应用于几个数据集（MNIST，COIL-20，COIL-100），并证明其在准确性和收敛速度方面的优越性。总之，本文的贡献有两个方面：（1）本文的主要贡献是自动编码器预训练阶段的一种新的优化方案，它鼓励一个符合聚类目标的判别潜在空间，并在聚类阶段前达到更高的精度。（2）一种新的聚类方案，其中在搜索最佳质心时增强潜在空间的判别力。

2 相关工作

我们在此提供了对当前已知的优化潜在空间来进行聚类的方法的简要回顾。 [15]提出DEC - 一种完全连接的堆叠自动编码器，通过最小化预训练阶段的重建损失来学习潜在的表示。应用于聚类阶段的目标函数是在模拟一个 t 分布的聚类软分配与从软分配构造的参考启发概率之间的Kullback Leibler（KL）散度。在[16]中，一个完全连接的自动编码器用k均值损失以及聚类阶段的重建损失训练。 [8]提出了DBC--一种完全卷积网络，具有层级批量正则化，旨在克服堆叠自动编码器的相对较慢的训练。 DBC使用与DEC相同的目标函数，其中有增强因子作为超参数，用于参考概率。 [17]介绍了JULE - 一种使用凝聚聚类方法以循环方式联合优化一个卷积神经网络和聚类参数的方法。在[5] VaDE中 - 提出了一种用于深度嵌入的变分自动编码器。一个生成模型，从中选择一个簇并选择一个潜在的表示，然后是一个深层网络，它将潜在的嵌入解码为可观察的。在[4]中，深度自动编码器被训练以最小化重建损失以及自表达层。该目标鼓励原始数据的稀疏表示。 [2]提出了DEPICT - 一种训练卷积自动编码器的方法，其中softmax层堆叠在编码器的最后层。 softmax条目表示每个数据点到每个簇的分配。最后，在[12]之后，[13]中提出了一种深度连续聚类方法。在该方法中，自动编码器参数与针对每个数据点定义的一组表示一起优化。通过最小化每个表示与其相关数据点之间的距离来优化表示，同时最小化表示之间的成对距离（类似于[1]提出的凸聚类方法）。他们应用非凸目标函数来惩罚表示之间的成对距离。然后将聚类确定为表示之间创建的图的连接组成。

3 判断聚类

在本文中，我们选择了一个范例，在该范例中，某个数据集的潜在空间表示与聚类参数一起被训练。 这种由最近的论文支持的端到端方法实现了面向聚类的表示，因此具有更好的聚类准确性。 在大多数论文中，自动编码器首先被训练以最小化重建损失，然后作为初始条件应用于联合优化问题，其中聚类和编码器参数被联合优化以最小化聚类误差。 然而，虽然主要关注的是聚类阶段，但我们观察到，在大多数情况下，聚集阶段对初始阶段的改善最多可达15％-20％的准确度。 这导致得出结论，初始阶段对总体准确性具有显著影响，因此应该聚焦这一步骤。

3.1 预训练阶段：获得判别潜在空间

让表示一个数据集，将被聚类成 K 个簇，让表示数据集中单个数据点，维度为 p。让

表示的潜在表示，编码器的参数表示为，。让

表示的重构结果，即解码器的输出，解码器的参数表示为。

我们提出了一系列成对判别函数，，表示任意的成对数据点相似度测量方式。

其中与原始数据点之间的相似性有关。 当先验知识不可用时，我们设置，其中代表数据集的势（元素个数）。 注意，（1）中具有的目标函数是次优的，因为它惩罚所有相似性，而不管它们是否属于不相同的簇。 显然，如果每个数据点的分配都可用，则被分成两组权重：一组用于最小化交叉簇的相似性，另一组用于簇内相似性的最大化，产生以下目标函数：

符号定义了一对数据点 i， j表示相同的簇C。分别表示簇之间和簇内的对数。 然而式（1）中关于的证明来自以下发现，考虑一个不受单个或几个簇支配的平衡数据集，那么D中的对数是 ，聚类内和聚类间的对数基数约为 和。 因此，与相似的对相比，有更多不相似的对。 注意，随着的增加而增加; 簇内对的数量约为所有数据对的。

根据等式（2）我们基于数据点的原始表示在数据点之间创建k-最近邻图。 然后将k-最近邻图中具有最大相似性的一部分对应用于等式（1）作为锚对，其相似性最大化。 锚点相似性的最大化指的是等式（2）的簇内部分。仅利用来自k-最近邻图的一小部分的原因是需要避免实际上不相似的对之间的相似性的最大化。 由于基于原始表示的相似性不可靠，我们仅使用具有最高置信度的对。 我们将A定义为锚对的集合，有

其中α<1是应用的超参数，以便补偿实际上不相似的锚对的不确定性。 设定作为归一化的潜在空间表示。 我们应用相似性度测量。 其中代表绝对值。 请注意，等式（4）是所有成对余弦相似度的加权L1范数。 我们选择L1而不是 L2，由于L1范数所鼓励的相似性的稀疏性（仅个非零元素）。

通常，数据集不能在主存储器中维护，并且通过随机梯度下降（SGD）对数据集B的批次执行训练，等式（4）应使用潜在表示的批量矩阵近似，其中表示批次的基数。 将定义为行归一化批量矩阵（其第i行是行向量），并且将定义为成对余弦相似度矩阵，使得。 此外，对于每个批次，构建一个k-最近邻图，并确定一组，产生以下对等式（4）的近似：

注意，C的对角线项是常数且等于1，因此不会影响优化。 此外，观察在右边的组成部分中，我们采用没有绝对值的和来鼓励值为1的相似性而不是具有值-1的不相似相反特征。

为了避免对数据点进行任意区分，我们建议对等式（5）随着重建损失进行规范化，产生以下优化问题：

其中λ代表正则化强度，表示重构损失，X代表原始输入批量矩阵，代表Frobenius范数。

3.2 聚类阶段：保持不相似

优化来自预训练阶段的后，将学习的自动编码器参数作为初始条件应用于聚类阶段。 在这一步中，我们联合优化编码器 - 解码器参数，质心；聚类目标的新优化变量。 用于聚类阶段的目标函数的自然候选者显然是所学习的质心与每个数据点之间的余弦相似性，因为应用余弦相似性来区分初始阶段中的数据点对。 因此，聚类阶段的主要目标是最大化以下目标函数

其中S代表分配矩阵和是群集过程的硬判决。 聚类阶段分为两个步骤：在第一步中，聚类分配尚不可信，因此聚类目标通过等式（6）保持正则化，其中权重由锚对确定。 在第二步，聚类分配被认为是可靠的，并且权重是根据聚类的分配来确定的。 因此，在第一步中解决的优化问题由下式给出：

其中分别代表判别和重建损失的正则化强度。 对于第二步，让我们定义每对簇之间的相似性度量，得到

请注意,等式（9）对最坏情况，即对具有最大相似性的一对簇进行处罚。 我们以同样的方式对待我们的内部目标

请注意，在等式（10）省略了绝对值，并且对于数据点对之间的余弦相似性的值1优先于-1。 第二步中的优化问题变为

其中分别代表簇间的和簇内的正则化强度，和重构损失。 

3.3 系统结构

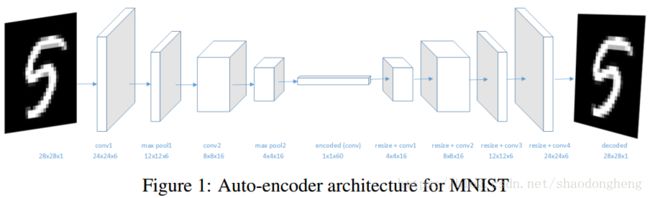
这里我们采用[8]提出的架构。我们的系统由两部分组成：深度判别自动编码器和聚类质心。 自动编码器网络是一个完全卷积的神经网络，卷积层具有relu激活，然后是批量归一化[3]和最大池化层。 解码器使用最近邻外推法将潜在空间上采样到更高分辨率，然后是[14]所述的批量标准卷积层。 自动编码器架构如图1所示。

3.4 训练策略

在初始阶段训练自动编码器从最小化方程（6）开始。 判别损失的正则化强度是一个超参数，。不同数据集之间的λ值不同，因此更复杂的数据集需要更积极的区分，同时保持重建损失的强度是恒常数。训练是在大批量上进行的，以确保。如1中所述，每个批次构建一个k-最近邻图，然后从图中提取一小组锚对和方程（6） 反向传播以优化自动编码器参数。自动编码器的训练方案总结在算法1中。

在聚类阶段，聚类变量与自动编码器参数联合优化。 我们应用交替最大化方案，其中每组变量被优化而其他组保持固定。 优化过程从的初始化开始，通过优化等式（7）基于整个数据集D.接下来，我们交替最大化分配矩阵S，然后最大化，最后最大化自动编码器参数。 优化过程迭代直到收敛。

聚类阶段分为两个阶段，这两个阶段通过他们最大化的目标函数彼此不同。 第一阶段的伪代码总结在算法2中。在第一阶段，我们优化等式（8），同时使用相对大的正则化强度用于判别损失和较低的正则化强度用于重建损失。 while循环指的是交替最大化方案，其中每组参数在几个时期内最大化。 对每个使用反向传播来执行优化。当超过最大迭代次数时或者当聚类目标在预定容差tol之上的连续迭代中没有改善时，终止进行。 注意，是超参数并且是数据集依赖的。

 第二阶段用来自第一阶段的参数初始化。 然后我们优化eq（11），其中，与前一阶段类似，将判别正则化强度设置为相对高的值，即，同时重构损失的正则化强度保持不变。 该过程迭代直到收敛。 每组变量的最大化是在几个时期内使用大批量的反向传播进行的。在两个阶段中，我们使用大批量，如在自动编码器训练阶段和几个时期。 聚类步骤的整个过程类似于算法2的伪代码，但现在使用eq（11）及其相关的超参数。

4 实验和结果