地理坐标和高斯投影坐标互相转换

        前言：原作者提供了js版本的坐标转换函数，和三种椭球体参数（北京54、西安80、WGS84），个人在百度上搜索了CGC2000坐标系的椭球参数，添加到函数里，使用java写的转换函数。在ArcMap里使用同一位置的两个不同坐标系的点进行验证，误差还算可以接受。。。

转换函数代码：

public class Convertor {
    private double a;//'椭球体长半轴
    private double b;// '椭球体短半轴
    private double f; //'扁率
    private double e;// '第一偏心率
    private double e1; //'第二偏心率
    private double FE;//'东偏移
    private double FN;//'北偏移
    private double L0;//'中央经度
    private double W0;//'原点纬线
    private double k0;//'比例因子
    /**
     * 幂函数
     * @param e
     * @param i
     * @return
     */
    private double MZ(double e, int i) {
        return Math.pow(e,i);
    }

    /**
     * 说明: 用于初始化转换参数
     *
     * @param TuoqiuCanshu    枚举类型，提供北京54、西安80和WGS84三个椭球参数
     * @param CentralMeridian 中央经线
     * @param OriginLatitude  原点纬度，如果是标准的分幅，则该参数是0
     * @param EastOffset      东偏移
     * @param NorthOffset     北偏移
     */
    public Convertor(int TuoqiuCanshu, double CentralMeridian, double OriginLatitude, double EastOffset, double NorthOffset) {
        /**
         * 'Krassovsky （北京54采用） 6378245 6356863.0188
         * 'IAG 75（西安80采用） 6378140 6356755.2882
         * 'WGS 84 6378137 6356752.3142
         * 'CGC 2000 6378137 6356752.31414
         */
        if (TuoqiuCanshu == 0)//北京五四
        {
            a = 6378245;
            b = 6356863.0188;
        } else if (TuoqiuCanshu == 1)// '西安八零
        {
            a = 6378140;
            b = 6356755.2882;
        }
        if (TuoqiuCanshu == 2)//'WGS84
        {
            a = 6378137;
            b = 6356752.3142;
        }
        if (TuoqiuCanshu == 3)//'CGC2000坐标
        {
            a = 6378137;
            b = 6356752.31414;
        }
        f = (a - b) / a;//扁率
        //e = Math.sqrt(1 - MZ((b / a) ,2));//'第一偏心率
        e = Math.sqrt(2 * f - MZ(f, 2));//'第一偏心率
        //eq = Math.sqrt(MZ((a / b) , 2) - 1);//'第二偏心率
        e1 = e / Math.sqrt(1 - MZ(e, 2));//'第二偏心率
        L0 = CentralMeridian;//中央经
        W0 = OriginLatitude;//原点纬线
        k0 = 1;//'比例因子
        FE = EastOffset;//东偏移
        FN = NorthOffset;//北偏移
    }

    /**
     * 经纬度坐标转高斯投影坐标
     * @param J 经度
     * @param W 纬度
     * @return
     */
    public double[] JWgetGK(double J, double W) {
        //'给出经纬度坐标，转换为高克投影坐标
        double[] resultP = new double[2];
        double BR = (W - W0) * Math.PI / 180;//纬度弧长
        double lo = (J - L0) * Math.PI / 180; //经差弧度
        double N = a / Math.sqrt(1 - MZ((e * Math.sin(BR)), 2)); //卯酉圈曲率半径
        //求解参数s
        double B0;
        double B2;
        double B4;
        double B6;
        double B8;
        double C = MZ(a, 2) / b;
        B0 = 1 - 3 * MZ(e1, 2) / 4 + 45 * MZ(e1, 4) / 64 - 175 * MZ(e1, 6) / 256 + 11025 * MZ(e1, 8) / 16384;
        B2 = B0 - 1;
        B4 = 15 / 32 * MZ(e1, 4) - 175 / 384 * MZ(e1, 6) + 3675 / 8192 * MZ(e1, 8);
        B6 = 0 - 35 / 96 * MZ(e1, 6) + 735 / 2048 * MZ(e1, 8);
        B8 = 315 / 1024 * MZ(e1, 8);
        double s = C * (B0 * BR + Math.sin(BR) * (B2 * Math.cos(BR) + B4 * MZ((Math.cos(BR)), 3) + B6 * MZ((Math.cos(BR)), 5) + B8 * MZ((Math.cos(BR)), 7)));
        double t = Math.tan(BR);
        double g = e1 * Math.cos(BR);
        double XR = s + MZ(lo, 2) / 2 * N * Math.sin(BR) * Math.cos(BR) + MZ(lo, 4) * N * Math.sin(BR) * MZ((Math.cos(BR)), 3) / 24 * (5 - MZ(t, 2) + 9 * MZ(g, 2) + 4 * MZ(g, 4)) + MZ(lo, 6) * N * Math.sin(BR) * MZ((Math.cos(BR)), 5) * (61 - 58 * MZ(t, 2) + MZ(t, 4)) / 720;
        double YR = lo * N * Math.cos(BR) + MZ(lo, 3) * N / 6 * MZ((Math.cos(BR)), 3) * (1 - MZ(t, 2) + MZ(g, 2)) + MZ(lo, 5) * N / 120 * MZ((Math.cos(BR)), 5) * (5 - 18 * MZ(t, 2) + MZ(t, 4) + 14 * MZ(g, 2) - 58 * MZ(g, 2) * MZ(t, 2));
        resultP[0] = YR + FE;
        resultP[1] = XR + FN;
        return resultP;
    }

    /**
     * 高斯投影坐标 转为 经纬度坐标
     * @param X 高斯投影坐标X
     * @param Y 高斯投影坐标Y
     * @return
     */
    public double[] GKgetJW(double X, double Y) {
        //'给出高克投影坐标，转换为经纬度坐标
        double[] resultP =new double[2];
        double El1 = (1 - Math.sqrt(1 - MZ(e, 2))) / (1 + Math.sqrt(1 - MZ(e, 2)));
        double Mf = (Y - FN) / k0;//真实坐标值
        double Q = Mf / (a * (1 - MZ(e, 2) / 4 - 3 * MZ(e, 4) / 64 - 5 * MZ(e, 6) / 256));//角度
        double Bf = Q + (3 * El1 / 2 - 27 * MZ(El1, 3) / 32) * Math.sin(2 * Q) + (21 * MZ(El1, 2) / 16 - 55 * MZ(El1, 4) / 32) * Math.sin(4 * Q) + (151 * MZ(El1, 3) / 96) * Math.sin(6 * Q) + 1097 / 512 * MZ(El1, 4) * Math.sin(8 * Q);
        double Rf = a * (1 - MZ(e, 2)) / Math.sqrt(MZ((1 - MZ((e * Math.sin(Bf)), 2)), 3));
        double Nf = a / Math.sqrt(1 - MZ((e * Math.sin(Bf)), 2));//卯酉圈曲率半径
        double Tf = MZ((Math.tan(Bf)), 2);
        double D = (X - FE) / (k0 * Nf);
        double Cf = MZ(e1, 2) * MZ((Math.cos(Bf)), 2);
        double B = Bf - Nf * Math.tan(Bf) / Rf * (MZ(D, 2) / 2 - (5 + 3 * Tf + 10 * Cf - 9 * Tf * Cf - 4 * MZ(Cf, 2) - 9 * MZ(e1, 2)) * MZ(D, 4) / 24 + (61 + 90 * Tf + 45 * MZ(Tf, 2) - 256 * MZ(e1, 2) - 3 * MZ(Cf, 2)) * MZ(D, 6) / 720);
        double L = L0 * Math.PI / 180 + 1 / Math.cos(Bf) * (D - (1 + 2 * Tf + Cf) * MZ(D, 3) / 6 + (5 - 2 * Cf + 28 * Tf - 3 * MZ(Cf, 2) + 8 * MZ(e1, 2) + 24 * MZ(Tf, 2)) * MZ(D, 5) / 120);
        double Bangle = B * 180 / Math.PI;
        double Langle = L * 180 / Math.PI;
        resultP[0] = Langle;//RW * 180 / Math.PI;
        resultP[1] = Bangle + W0;//RJ * 180 / Math.PI;
        return resultP;
    }
}

测试代码：

public class Main {
    public static void main(String[] args) {
        Convertor convertor = new Convertor(1, 120, 0, 500000, 0);
        double[] gk = convertor.JWgetGK(120.101099, 36.010338);
        double[] jw = convertor.GKgetJW(509114.252958,3986696.370605);
        System.out.println(gk[0]+","+gk[1]);
        System.out.println(jw[0]+","+jw[1]);
    }
}

 

 

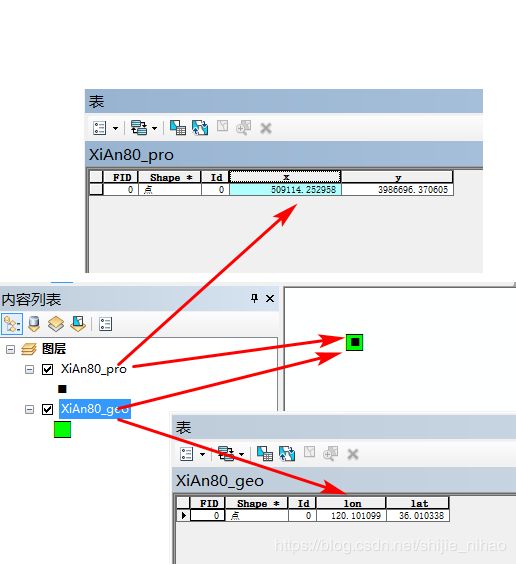
结果验证： 

        两个表示同一位置的不同坐标系（西安80地理系，西安80高斯投影系）的，坐标值经过上面的代码转换后的结果和经过arcmap转换的坐标值的误差还可以接受。