【模型压缩】训练时量化--training aware quantization

本文来自谷歌CVPR2018的文章：
Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
代码已经在tensorflow中集成了
https://github.com/tensorflow/tensorflow/tree/master/tensorflow/contrib/quantize

前情提要

量化一般分为post-quantization，和training-aware-quantization。

• post-quantization是直接训练出一个浮点模型直接对模型的参数进行直接量化。这种方法比较常见于对一个大模型进量化，而对小模型会导致大幅度的性能降低。主要原因有两个：1）post-training对参数取值的要求需要比较大的范围。如果参数的取值范围比较小，在量化过程中非常容易导致很高的相对误差。2）量化后的权重中的一些异常的权重会导致模型参数量的降低。

• training-aware-quantization是在训练中模拟量化行为，在训练中用浮点来保存定点参数，最后inference的时候，直接采用定点参数。

本文的量化方法

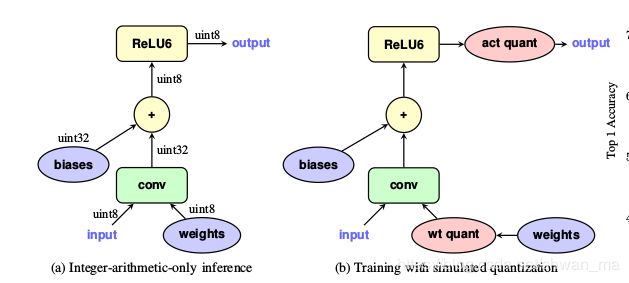
量化算法核心在于，将一个浮点数r量化成uint8的q，其中Z为zero point，用于非对称量化（uint8），S为scale，缩放因子（浮点）。
$$r=S(q-Z)$$

量化的数据结构：

template<typename Qtype>     //e.g. uint8
struct QuantizationBuffer{
	vector<Qtype> q;         // 定点
	float S;                 // scale
	Qtype Z;                 // zero-point
}

注意本文对网络的weights进行量化至8位，bias仍然保留32位浮点，用于对量化精度的补偿。

对于上图的量化表述：
（a） 测试时量化后的inference计算，uint8代替float去进行矩阵乘法用于加速
（b）训练时，加入Quantization的OP于计算图中，训练过程仍然是浮点计算，通过op去模拟定点。

如何利用uint8进行前向加速

uint8的矩阵乘法要远远要比浮点矩阵乘法高效。从上文知道，一个浮点可以表示为$r=S(q-Z)$，两个浮点的乘法为：

$$S_3(q_3^{(i,k)}-Z_3)=\sum _{j=1}^N{S}_1(q_1^{(i,k)}-Z_1)S_1(q_1^{(i,k)}-Z_1)$$
化简为：
$$q_3^{(i,k)}=Z_3+M\sum _{j=1}^N(q_1^{(i,j)}-Z_1)(q_2^{(i,j)}-Z_2)$$
其中 $M=\frac{S_1{S}_2}{S_3}$。对上述进行进一步拆分为：
$$q_3^{(i,k)}=Z_3+M(N{Z}_1{Z}_2-Z_1{a}_2^k-Z_2{a}_1^k+\sum _{j=1}^N{q}_1^{(i,j)}{q}_2^{(j,k)})$$
其中$a_2^k={\sum }_{j=1}^N{q}_2^{(j,k)},a_1^k={\sum }_{j=1}^N{q}_1^{(j,k)}$

那么计算量将大部分留在了uint8的定点乘法：
$$\sum _{j=1}^N{q}_1^{(i,j)}{q}_2^{(j,k)}$$, 相比于一开始，我们则不需要进行减法操作，对uint8进行扩充到16位或者以上。

训练时的量化op

当进入量化op时

1. 第一步进行截断
   $$clamp(r;a,b)=min(max(x,a),b)$$
2. 第二步进行非对称量化
   $$s(a,b,n)=\frac{b-a}{n-1}$$
3. 第三步将量化后的数据进行浮点化（反量化）
   $$q(r;a,b,n)=\frac{clamp(r;a,b)-a}{s(a,b,n)}s(a,b,n)+a$$

BN的量化实现

此处对于BN，inference中，我们将BN的权重折合到卷积中。
回忆一下，对于BN的inference：
$$\gamma \frac{input-EMA(\mu )}{\sqrt{EMA({\sigma }^2)}}+\beta$$

在量化行为中：
BN的w将折合到卷积中：
$$w=\gamma \frac{w}{\sqrt{EMA({\sigma }^2)}}$$

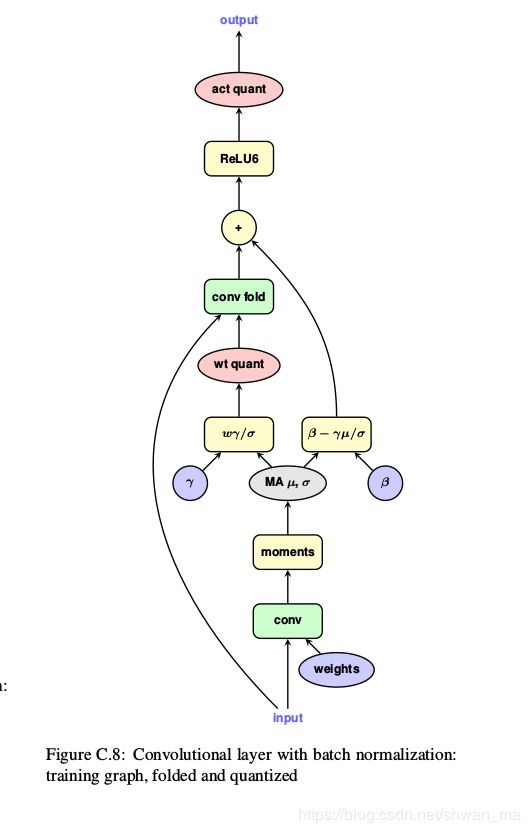
tensorflow 实现