利用分治法解决凸包问题

凸包的意思就是包含所有给定点的凸多边形。

输入一组已经制定x，y坐标的点。输出是这组点的凸包。

例子：

Input : points[] = {(0, 0), (0, 4), (-4, 0), (5, 0), (0, -6), (1, 0)};
Output : (-4, 0), (5, 0), (0, -6), (0, 4)

预备知识：

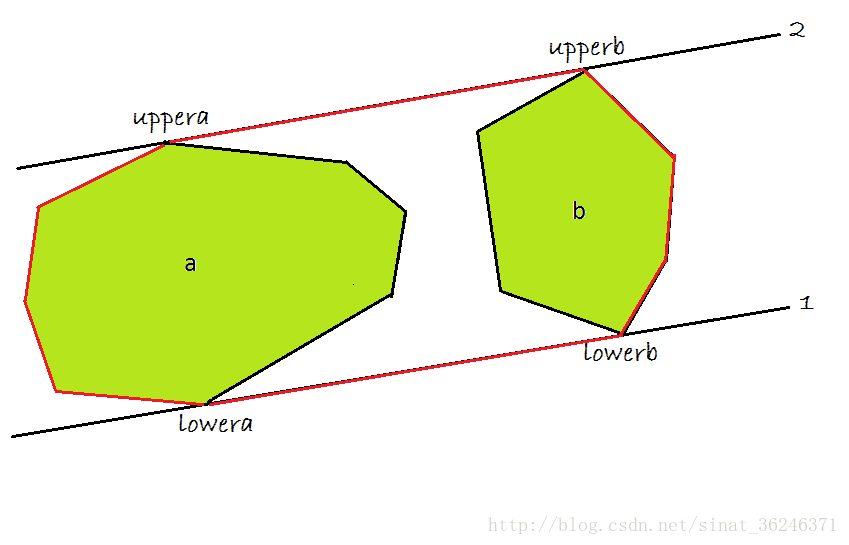
两个凸多边形之间的切线。

算法：

已知一个点集合，我们已经知道了它们的凸包。假设我们已经知道了左半部分和右半部分的凸包，那么现在的问题就变成了合并这两个凸包，并且确定整个集合的凸包。

这一步可以通过找到左右两个凸包的上下切线来搞定。这就是两个凸多边形之间的切线。

设左边的凸包为a，右边的凸包为b。于是下面的切线和上面的切线分别为1和2，如图所示。

然后红线画出了最后的凸包。

现在问题还没完全解决，我们如何才能找到左右整个的凸包呢？这里递归在图中出现了，我们可以把集合中的点分区，直到每个集合中的点的数目都非常小，例如5个点，然后我们就可以通过暴力法找到这个集合的凸包了。对于整个集合的点，在合并的过程中就可以得到整个凸包。

注意：

我们已经用暴力算法来得到小集合的点的凸包了，这一步的时间复杂度是 O(n3) 。但是有些人建议这么做，一个3个或者更少的点集的凸包就是整个点集。这个一般来说没问题，但是当我们要合并一个两个点的左凸包和3个点的右凸包的时候，在一些特殊情况下程序就会陷入无限的循环。所以为了解决这个问题，我们可以在 O(n3) 的时间内直接找到5个或者更少点的凸包，这个做法虽然数字大了点，但是不影响算法的整体时间复杂度。

// A divide and conquer program to find convex
// hull of a given set of points.
#include 
#include 
#include 
#include 
using namespace std;

// stores the center of polygon (It is made
// global becuase it is used in comare function)
pair<int, int> mid;

// determines the quadrant of a point
// (used in compare())
int quad(pair<int, int> p) {
    if (p.first >= 0 && p.second >= 0)
        return 1;
    if (p.first <= 0 && p.second >= 0)
        return 2;
    if (p.first <= 0 && p.second <= 0)
        return 3;
    return 4;
}

// Checks whether the line is crossing the polygon
int orientation(pair<int, int> a, pair<int, int> b,
    pair<int, int> c) {
    int res = (b.second - a.second)*(c.first - b.first) -
        (c.second - b.second)*(b.first - a.first);

    if (res == 0)
        return 0;
    if (res > 0)
        return 1;
    return -1;
}

// compare function for sorting
bool compare(pair<int, int> p1, pair<int, int> q1) {
    pair<int, int> p = make_pair(p1.first - mid.first,
        p1.second - mid.second);
    pair<int, int> q = make_pair(q1.first - mid.first,
        q1.second - mid.second);

    int one = quad(p);
    int two = quad(q);

    if (one != two)
        return (one < two);
    return (p.second*q.first < q.second*p.first);
}

// Finds upper tangent of two polygons 'a' and 'b'
// represented as two vectors.
vectorint, int>> merger(vectorint, int> > a,
    vectorint, int> > b) {
    // n1 -> number of points in polygon a
    // n2 -> number of points in polygon b
    int n1 = a.size(), n2 = b.size();

    int ia = 0, ib = 0;
    for (int i = 1; iif (a[i].first > a[ia].first)
            ia = i;

    // ib -> leftmost point of b
    for (int i = 1; iif (b[i].first < b[ib].first)
            ib = i;

    // finding the upper tangent
    int inda = ia, indb = ib;
    bool done = 0;
    while (!done) {
        done = 1;
        while (orientation(b[indb], a[inda], a[(inda + 1) % n1]) >= 0)
            inda = (inda + 1) % n1;

        while (orientation(a[inda], b[indb], b[(n2 + indb - 1) % n2]) <= 0) {
            indb = (n2 + indb - 1) % n2;
            done = 0;
        }
    }

    int uppera = inda, upperb = indb;
    inda = ia, indb = ib;
    done = 0;
    int g = 0;
    while (!done)//finding the lower tangent
    {
        done = 1;
        while (orientation(a[inda], b[indb], b[(indb + 1) % n2]) >= 0)
            indb = (indb + 1) % n2;

        while (orientation(b[indb], a[inda], a[(n1 + inda - 1) % n1]) <= 0) {
            inda = (n1 + inda - 1) % n1;
            done = 0;
        }
    }

    int lowera = inda, lowerb = indb;
    vectorint, int>> ret;

    //ret contains the convex hull after merging the two convex hulls
    //with the points sorted in anti-clockwise order
    int ind = uppera;
    ret.push_back(a[uppera]);
    while (ind != lowera) {
        ind = (ind + 1) % n1;
        ret.push_back(a[ind]);
    }

    ind = lowerb;
    ret.push_back(b[lowerb]);
    while (ind != upperb) {
        ind = (ind + 1) % n2;
        ret.push_back(b[ind]);
    }
    return ret;

}

// Brute force algorithm to find convex hull for a set
// of less than 6 points
vectorint, int>> bruteHull(vectorint, int>> a) {
    // Take any pair of points from the set and check
    // whether it is the edge of the convex hull or not.
    // if all the remaining points are on the same side
    // of the line then the line is the edge of convex
    // hull otherwise not
    setint, int> > s;

    for (int i = 0; ifor (int j = i + 1; jint x1 = a[i].first, x2 = a[j].first;
            int y1 = a[i].second, y2 = a[j].second;

            int a1 = y1 - y2;
            int b1 = x2 - x1;
            int c1 = x1*y2 - y1*x2;
            int pos = 0, neg = 0;
            for (int k = 0; kif (a1*a[k].first + b1*a[k].second + c1 <= 0)
                    neg++;
                if (a1*a[k].first + b1*a[k].second + c1 >= 0)
                    pos++;
            }
            if (pos == a.size() || neg == a.size()) {
                s.insert(a[i]);
                s.insert(a[j]);
            }
        }
    }

    vectorint, int>>ret;
    for (auto e : s)
        ret.push_back(e);

    // Sorting the points in the anti-clockwise order
    mid = { 0, 0 };
    int n = ret.size();
    for (int i = 0; ifor (int i = 0; ireturn ret;
}

// Returns the convex hull for the given set of points
vectorint, int>> divide(vectorint, int>> a) {
    // If the number of points is less than 6 then the
    // function uses the brute algorithm to find the
    // convex hull
    if (a.size() <= 5)
        return bruteHull(a);

    // left contains the left half points
    // right contains the right half points
    vectorint, int>>left, right;
    for (int i = 0; i2; i++)
        left.push_back(a[i]);
    for (int i = a.size() / 2; i// convex hull for the left and right sets
    vectorint, int>>left_hull = divide(left);
    vectorint, int>>right_hull = divide(right);

    // merging the convex hulls
    return merger(left_hull, right_hull);
}

// Driver code
int main() {
    vectorint, int> > a;
    a.push_back(make_pair(0, 0));
    a.push_back(make_pair(1, -4));
    a.push_back(make_pair(-1, -5));
    a.push_back(make_pair(-5, -3));
    a.push_back(make_pair(-3, -1));
    a.push_back(make_pair(-1, -3));
    a.push_back(make_pair(-2, -2));
    a.push_back(make_pair(-1, -1));
    a.push_back(make_pair(-2, -1));
    a.push_back(make_pair(-1, 1));

    int n = a.size();

    // sorting the set of points according
    // to the x-coordinate
    sort(a.begin(), a.end());
    vectorint, int> >ans = divide(a);

    cout << "convex hull:\n";
    for (auto e : ans)
        cout << e.first << " "
        << e.second << endl;

    return 0;
}

输出：

Convex Hull:
-5 -3
-1 -5
1 -4
0 0
-1 1

时间复杂度：
因为我们要把点集分成两个相等的部分，所以合并左右凸包的时间复杂度是 O(n) ，所以上述算法时间复杂度是 O(nlogn) 。

相关文章：

Convex Hull | Set 1 (Jarvis’s Algorithm or Wrapping)
Convex Hull | Set 2 (Graham Scan)
Quickhull Algorithm for Convex Hull