[数字信号处理]IIR滤波器的间接设计(C代码)
1.模拟滤波器的设计
1.1巴特沃斯滤波器的次数
根据给定的参数设计模拟滤波器,然后进行变数变换,求取数字滤波器的方法,称为滤波器的间接设计。做为数字滤波器的设计基础的模拟滤波器,称之为原型滤波器。这里,我们首先介绍的是最简单最基础的原型滤波器,巴特沃斯低通滤波器。由于IIR滤波器不具有线性相位特性,因此不必考虑相位特性,直接考虑其振幅特性。
在这里,N是滤波器的次数,Ωc是截止频率。从上式的振幅特性可以看出,这个是单调递减的函数,其振幅特性是不存在纹波的。设计的时候,一般需要先计算跟所需要设计参数相符合的次数N。首先,就需要先由阻带频率,计算出阻带衰减
将巴特沃斯低通滤波器的振幅特性,直接带入上式,则有
最后,可以解得次数N为
当然,这里的N只能为正数,因此,若结果为小数,则舍弃小数,向上取整。
1.2巴特沃斯滤波器的传递函数
巴特沃斯低通滤波器的传递函数,可由其振幅特性的分母多项式求得。其分母多项式
根据S解开,可以得到极点。这里,为了方便处理,我们分为两种情况去解这个方程。当N为偶数的时候,
同样的,这里也使用了欧拉公式。归纳以上,极点的解为
上式所求得的极点,是在s平面内,在半径为Ωc的圆上等间距的点,其数量为2N个。为了使得其IIR滤波器稳定,那么,只能选取极点在S平面左半平面的点。选定了稳定的极点之后,其模拟滤波器的传递函数就可由下式求得。
1.3巴特沃斯滤波器的实现(C语言)
首先,是次数的计算。次数的计算,我们可以由下式求得。
其对应的C语言程序为
N = Ceil(0.5*( log10 ( pow (10, Stopband_attenuation/10) - 1) /
log10 (Stopband/Cotoff) ));然后是极点的选择,这里由于涉及到复数的操作,我们就声明一个复数结构体就可以了。最重要的是,极点的计算含有自然指数函数,这点对于计算机来讲,不是太方便,所以,我们将其替换为三角函数,
这样的话,实部与虚部就还可以分开来计算。其代码实现为
typedef struct
{
double Real_part;
double Imag_Part;
} COMPLEX;
COMPLEX poles[N];
for(k = 0;k <= ((2*N)-1) ; k++)
{
if(Cotoff*cos((k+dk)*(pi/N)) < 0)
{
poles[count].Real_part = -Cotoff*cos((k+dk)*(pi/N));
poles[count].Imag_Part= -Cotoff*sin((k+dk)*(pi/N));
count++;
if (count == N) break;
}
} 计算出稳定的极点之后,就可以进行传递函数的计算了。传递的函数的计算,就像下式一样
这里,为了得到模拟滤波器的系数,需要将分母乘开。很显然,这里的极点不一定是整数,或者来说,这里的乘开需要做复数运算。其复数的乘法代码如下,
int Complex_Multiple(COMPLEX a,COMPLEX b,
double *Res_Real,double *Res_Imag)
{
*(Res_Real) = (a.Real_part)*(b.Real_part) - (a.Imag_Part)*(b.Imag_Part);
*(Res_Imag)= (a.Imag_Part)*(b.Real_part) + (a.Real_part)*(b.Imag_Part);
return (int)1;
}将其乘开,其大致的关系就像下图所示一样。
计算的关系一目了然,这样的话,实现就简单多了。高阶的情况下也一样,重复这种计算就可以了。其代码为
Res[0].Real_part = poles[0].Real_part;
Res[0].Imag_Part= poles[0].Imag_Part;
Res[1].Real_part = 1;
Res[1].Imag_Part= 0;
for(count_1 = 0;count_1 < N-1;count_1++)
{
for(count = 0;count <= count_1 + 2;count++)
{
if(0 == count)
{
Complex_Multiple(Res[count], poles[count_1+1],
&(Res_Save[count].Real_part),
&(Res_Save[count].Imag_Part));
}
else if((count_1 + 2) == count)
{
Res_Save[count].Real_part += Res[count - 1].Real_part;
Res_Save[count].Imag_Part += Res[count - 1].Imag_Part;
}
else
{
Complex_Multiple(Res[count], poles[count_1+1],
&(Res_Save[count].Real_part),
&(Res_Save[count].Imag_Part));
1 Res_Save[count].Real_part += Res[count - 1].Real_part;
Res_Save[count].Imag_Part += Res[count - 1].Imag_Part;
}
}
*(b+N) = *(a+N);
}2.双1次z变换
2.1双1次z变换的原理
我们为了将模拟滤波器转换为数字滤波器的,可以用的方法很多。这里着重说说双1次z变换。我们希望通过双1次z变换,建立一个s平面到z平面的映射关系,将模拟滤波器转换为数字滤波器。
和之前的例子一样,我们假设有如下模拟滤波器的传递函数。
将其做拉普拉斯逆变换,可得到其时间域内的连续微分方程式,
其中,x(t)表示输入,y(t)表示输出。然后我们需要将其离散化,假设其采样周期是T,用差分方程去近似的替代微分方程,可以得到下面结果
然后使用z变换,再将其化简。可得到如下结果
从而,我们可以得到了s平面到z平面的映射关系,即
由于所有的高阶系统都可以视为一阶系统的并联,所以,这个映射关系在高阶系统中,也是成立的。
然后,将关系式
带入上式,可得
到这里,我们可以就可以得到Ω与ω的对应关系了。
这里的Ω与ω的对应关系很重要。我们最终的目的设计的是数字滤波器,所以,设计时候给的参数必定是数字滤波器的指标。而我们通过间接设计设计IIR滤波器时候,首先是要设计模拟滤波器,再通过变换,得到数字滤波器。那么,我们首先需要做的,就是将数字滤波器的指标,转换为模拟滤波器的指标,基于这个指标去设计模拟滤波器。另外,这里的采样时间T的取值很随意,为了方便计算,一般取1s就可以。
可以看出,我们还是需要将式子乘开,进行合并同类项,这个跟之前说的算法相差不大。其代码为。
for(Count = 0;Count<=N;Count++)
{
for(Count_Z = 0;Count_Z <= N;Count_Z++)
{
Res[Count_Z] = 0;
Res_Save[Count_Z] = 0;
}
Res_Save [0] = 1;
for(Count_1 = 0; Count_1 < N-Count;Count_1++)
{
for(Count_2 = 0; Count_2 <= Count_1+1;Count_2++)
{
if(Count_2 == 0) Res[Count_2] += Res_Save[Count_2];
else if((Count_2 == (Count_1+1))&&(Count_1 != 0))
Res[Count_2] += -Res_Save[Count_2 - 1];
else Res[Count_2] += Res_Save[Count_2] - Res_Save[Count_2 - 1];
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
Res_Save[Count_Z] = Res[Count_Z] ;
Res[Count_Z] = 0;
}
}
for(Count_1 = (N-Count); Count_1 < N;Count_1++)
{
for(Count_2 = 0; Count_2 <= Count_1+1;Count_2++)
{
if(Count_2 == 0) Res[Count_2] += Res_Save[Count_2];
else if((Count_2 == (Count_1+1))&&(Count_1 != 0))
Res[Count_2] += Res_Save[Count_2 - 1];
else
Res[Count_2] += Res_Save[Count_2] + Res_Save[Count_2 - 1];
}
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
Res_Save[Count_Z] = Res[Count_Z] ;
Res[Count_Z] = 0;
}
}
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
*(az+Count_Z) += pow(2,N-Count) * (*(as+Count)) *
Res_Save[Count_Z];
*(bz+Count_Z) += (*(bs+Count)) * Res_Save[Count_Z];
}
}
3.IIR滤波器的间接设计代码(C语言)
#include
#include
#include
#include
#define pi ((double)3.1415926)
struct DESIGN_SPECIFICATION
{
double Cotoff;
double Stopband;
double Stopband_attenuation;
};
typedef struct
{
double Real_part;
double Imag_Part;
} COMPLEX;
int Ceil(double input)
{
if(input != (int)input) return ((int)input) +1;
else return ((int)input);
}
int Complex_Multiple(COMPLEX a,COMPLEX b
,double *Res_Real,double *Res_Imag)
{
*(Res_Real) = (a.Real_part)*(b.Real_part) - (a.Imag_Part)*(b.Imag_Part);
*(Res_Imag)= (a.Imag_Part)*(b.Real_part) + (a.Real_part)*(b.Imag_Part);
return (int)1;
}
int Buttord(double Cotoff,
double Stopband,
double Stopband_attenuation)
{
int N;
printf("Wc = %lf [rad/sec] \n" ,Cotoff);
printf("Ws = %lf [rad/sec] \n" ,Stopband);
printf("As = %lf [dB] \n" ,Stopband_attenuation);
printf("--------------------------------------------------------\n" );
N = Ceil(0.5*( log10 ( pow (10, Stopband_attenuation/10) - 1) /
log10 (Stopband/Cotoff) ));
return (int)N;
}
int Butter(int N, double Cotoff,
double *a,
double *b)
{
double dk = 0;
int k = 0;
int count = 0,count_1 = 0;
COMPLEX poles[N];
COMPLEX Res[N+1],Res_Save[N+1];
if((N%2) == 0) dk = 0.5;
else dk = 0;
for(k = 0;k <= ((2*N)-1) ; k++)
{
if(Cotoff*cos((k+dk)*(pi/N)) < 0)
{
poles[count].Real_part = -Cotoff*cos((k+dk)*(pi/N));
poles[count].Imag_Part= -Cotoff*sin((k+dk)*(pi/N));
count++;
if (count == N) break;
}
}
printf("Pk = \n" );
for(count = 0;count < N ;count++)
{
printf("(%lf) + (%lf i) \n" ,-poles[count].Real_part
,-poles[count].Imag_Part);
}
printf("--------------------------------------------------------\n" );
Res[0].Real_part = poles[0].Real_part;
Res[0].Imag_Part= poles[0].Imag_Part;
Res[1].Real_part = 1;
Res[1].Imag_Part= 0;
for(count_1 = 0;count_1 < N-1;count_1++)
{
for(count = 0;count <= count_1 + 2;count++)
{
if(0 == count)
{
Complex_Multiple(Res[count], poles[count_1+1],
&(Res_Save[count].Real_part),
&(Res_Save[count].Imag_Part));
//printf( "Res_Save : (%lf) + (%lf i) \n" ,Res_Save[0].Real_part,Res_Save[0].Imag_Part);
}
else if((count_1 + 2) == count)
{
Res_Save[count].Real_part += Res[count - 1].Real_part;
Res_Save[count].Imag_Part += Res[count - 1].Imag_Part;
}
else
{
Complex_Multiple(Res[count], poles[count_1+1],
&(Res_Save[count].Real_part),
&(Res_Save[count].Imag_Part));
//printf( "Res : (%lf) + (%lf i) \n" ,Res[count - 1].Real_part,Res[count - 1].Imag_Part);
//printf( "Res_Save : (%lf) + (%lf i) \n" ,Res_Save[count].Real_part,Res_Save[count].Imag_Part);
Res_Save[count].Real_part += Res[count - 1].Real_part;
Res_Save[count].Imag_Part += Res[count - 1].Imag_Part;
//printf( "Res_Save : (%lf) + (%lf i) \n" ,Res_Save[count].Real_part,Res_Save[count].Imag_Part);
}
//printf("There \n" );
}
for(count = 0;count <= N;count++)
{
Res[count].Real_part = Res_Save[count].Real_part;
Res[count].Imag_Part= Res_Save[count].Imag_Part;
*(a + N - count) = Res[count].Real_part;
}
//printf("There!! \n" );
}
*(b+N) = *(a+N);
//------------------------display---------------------------------//
printf("bs = [" );
for(count = 0;count <= N ;count++)
{
printf("%lf ", *(b+count));
}
printf(" ] \n" );
printf("as = [" );
for(count = 0;count <= N ;count++)
{
printf("%lf ", *(a+count));
}
printf(" ] \n" );
printf("--------------------------------------------------------\n" );
return (int) 1;
}
int Bilinear(int N,
double *as,double *bs,
double *az,double *bz)
{
int Count = 0,Count_1 = 0,Count_2 = 0,Count_Z = 0;
double Res[N+1];
double Res_Save[N+1];
for(Count_Z = 0;Count_Z <= N;Count_Z++)
{
*(az+Count_Z) = 0;
*(bz+Count_Z) = 0;
}
for(Count = 0;Count<=N;Count++)
{
for(Count_Z = 0;Count_Z <= N;Count_Z++)
{
Res[Count_Z] = 0;
Res_Save[Count_Z] = 0;
}
Res_Save [0] = 1;
for(Count_1 = 0; Count_1 < N-Count;Count_1++)
{
for(Count_2 = 0; Count_2 <= Count_1+1;Count_2++)
{
if(Count_2 == 0)
{
Res[Count_2] += Res_Save[Count_2];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
else if((Count_2 == (Count_1+1))&&(Count_1 != 0))
{
Res[Count_2] += -Res_Save[Count_2 - 1];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
else
{
Res[Count_2] += Res_Save[Count_2] - Res_Save[Count_2 - 1];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
}
//printf( "Res : ");
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
Res_Save[Count_Z] = Res[Count_Z] ;
Res[Count_Z] = 0;
//printf( "[%d] %lf " ,Count_Z, Res_Save[Count_Z]);
}
//printf(" \n" );
}
for(Count_1 = (N-Count); Count_1 < N;Count_1++)
{
for(Count_2 = 0; Count_2 <= Count_1+1;Count_2++)
{
if(Count_2 == 0)
{
Res[Count_2] += Res_Save[Count_2];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
else if((Count_2 == (Count_1+1))&&(Count_1 != 0))
{
Res[Count_2] += Res_Save[Count_2 - 1];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
else
{
Res[Count_2] += Res_Save[Count_2] + Res_Save[Count_2 - 1];
//printf( "Res[%d] %lf \n" , Count_2 ,Res[Count_2]);
}
}
// printf( "Res : ");
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
Res_Save[Count_Z] = Res[Count_Z] ;
Res[Count_Z] = 0;
//printf( "[%d] %lf " ,Count_Z, Res_Save[Count_Z]);
}
//printf(" \n" );
}
//printf( "Res : ");
for(Count_Z = 0;Count_Z<= N;Count_Z++)
{
*(az+Count_Z) += pow(2,N-Count) * (*(as+Count)) * Res_Save[Count_Z];
*(bz+Count_Z) += (*(bs+Count)) * Res_Save[Count_Z];
//printf( " %lf " ,*(bz+Count_Z));
}
//printf(" \n" );
}
for(Count_Z = N;Count_Z >= 0;Count_Z--)
{
*(bz+Count_Z) = (*(bz+Count_Z))/(*(az+0));
*(az+Count_Z) = (*(az+Count_Z))/(*(az+0));
}
//------------------------display---------------------------------//
printf("bz = [" );
for(Count_Z= 0;Count_Z <= N ;Count_Z++)
{
printf("%lf ", *(bz+Count_Z));
}
printf(" ] \n" );
printf("az = [" );
for(Count_Z= 0;Count_Z <= N ;Count_Z++)
{
printf("%lf ", *(az+Count_Z));
}
printf(" ] \n" );
printf("--------------------------------------------------------\n" );
return (int) 1;
}
int main(void)
{
int count;
struct DESIGN_SPECIFICATION IIR_Filter;
IIR_Filter.Cotoff = (double)(pi/2); //[red]
IIR_Filter.Stopband = (double)((pi*3)/4); //[red]
IIR_Filter.Stopband_attenuation = 30; //[dB]
int N;
IIR_Filter.Cotoff = 2 * tan((IIR_Filter.Cotoff)/2); //[red/sec]
IIR_Filter.Stopband = 2 * tan((IIR_Filter.Stopband)/2); //[red/sec]
N = Buttord(IIR_Filter.Cotoff,
IIR_Filter.Stopband,
IIR_Filter.Stopband_attenuation);
printf("N: %d \n" ,N);
printf("--------------------------------------------------------\n" );
double as[N+1] , bs[N+1];
Butter(N,
IIR_Filter.Cotoff,
as,
bs);
double az[N+1] , bz[N+1];
Bilinear(N,
as,bs,
az,bz);
printf("Finish \n" );
return (int)0;
}
3.间接设计实现的IIR滤波器的性能
使用上述程序,gcc编译通过,执行结果如下。
其频率响应如下所示。博客地址: http://blog.csdn.net/thnh169/
![[数字信号处理]IIR滤波器的间接设计(C代码)_第1张图片](http://img.e-com-net.com/image/info8/34b1a5910cfa40e4bebd8b80f5f98c7a.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第2张图片](http://img.e-com-net.com/image/info8/1be541b649c040769933074dacf7a47e.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第3张图片](http://img.e-com-net.com/image/info8/a6aea21a404d49488a2e9a55b66ab8c9.jpg)
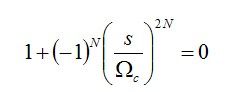
![[数字信号处理]IIR滤波器的间接设计(C代码)_第4张图片](http://img.e-com-net.com/image/info8/1c30b3b7578949d2ab8a749f6f783324.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第5张图片](http://img.e-com-net.com/image/info8/146c130891cb4e42a58f1822bca67c74.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第6张图片](http://img.e-com-net.com/image/info8/f080e60f57b84bd7bd7e8b434dac8fdb.jpg)
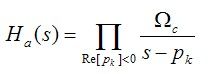
![[数字信号处理]IIR滤波器的间接设计(C代码)_第8张图片](http://img.e-com-net.com/image/info8/b3a54abb788747e78e918b1bb862d0ba.jpg)
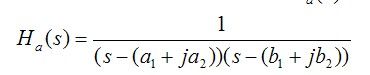
![[数字信号处理]IIR滤波器的间接设计(C代码)_第9张图片](http://img.e-com-net.com/image/info8/42b46e58024d4018915450594ae3e1b8.jpg)
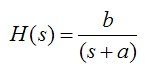
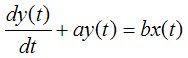

![[数字信号处理]IIR滤波器的间接设计(C代码)_第10张图片](http://img.e-com-net.com/image/info8/15e9928414ae4f29a7c499db401725ad.jpg)
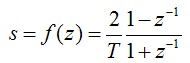
![[数字信号处理]IIR滤波器的间接设计(C代码)_第11张图片](http://img.e-com-net.com/image/info8/e07707b8148d43d790029a46c97dce05.jpg)
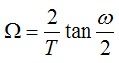

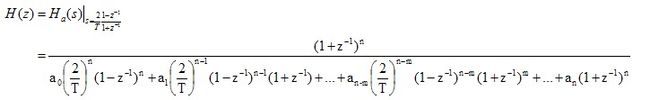
![[数字信号处理]IIR滤波器的间接设计(C代码)_第12张图片](http://img.e-com-net.com/image/info8/3df1ed4fe10c4c2c895b09369e789921.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第13张图片](http://img.e-com-net.com/image/info8/18aa2e02969844059d46bd81f6fbc8eb.jpg)
![[数字信号处理]IIR滤波器的间接设计(C代码)_第14张图片](http://img.e-com-net.com/image/info8/09d0501373f34a8993cd8a42528646dd.jpg)