包教包会!十分钟搞定自顶向下分析——编译原理速成计划
文章目录
- 一、总述
- 二、流程介绍
- 三、原理说明+如何做题
- 0.我们想干啥
- 1.剔除多余规则和有害规则
- 原理说明
- 如何做题
- 2.提取左公因子(消除回溯)和消除左递归
- 原理说明
- 如何做题
- 3.哪些非终结符能推出空
- 原理说明
- 如何做题
- 4.求FIRST集
- 原理说明
- 如何做题
- 5.求FOLLOW集
- 原理说明
- 如何做题
- 6.求SELECT集(可以不弄,视你的教材决定)
- 原理说明
- 如何做题
- 7.判断是不是LL(1)文法
- 原理说明
- 如何做题
- 8.预测分析表
- 原理说明
- 如何做题
- 9.判断句子是否能被接受
- 原理说明+如何做题
- 四、结语
一、总述
第一次学自顶向下分析的我曾经也面对书上各种奇怪的集而苦恼,总感觉非常难而且容易算漏,但是经过我对整个流程进行了一次代码实现后我对它有了更深刻的理解,并总结出了如何快速做出这些题目以及这些流程背后的原理,来跟大家一起分享~
为了照顾要期末考试的童鞋萌需要用最短时间学会咋做题,所以只想知道怎么做出题目,但是对原理不太深究的童鞋可以略过原理部分,直接看如何做题的部分,基本能在十分钟内学会做这种类型的题,想明白为什么自顶向下分析需要做这些东西,以及它到底在干什么的童鞋可能需要多花一点点时间看前面的部分噢~
二、流程介绍
可能看着很麻烦,其实非常简单!!肯定能学会!!请大家务必看下去!!!
首先第一步要做的是剔除多余规则和有害规则,然后提取左公因子(消除回溯)和消除左递归,接着求出哪些非终结符能推出空(这一步用可以为后面求集带来方便),接着求FIRST集和FOLLOW集,然后求SELECT集(也可以不用求,有只用FIRST集和FOLLOW集的方法,视你的教材而定),判断是否是LL(1)文法,接下来得到预测分析表,就能通过预测分析表来确定给定的句子能不能被接受啦~
三、原理说明+如何做题
0.我们想干啥
- 我们想要一个LL(1)文法,然后判断一个句子是否能被LL(1)文法接受。
LL(1)的含义为:第一个L表明自顶向下分析时从左向右扫描输入串,第二个L表明分析过程将最左推导,1表明只需向右看一个符号便可决定如何推导,即选择那个产生式进行推导。
说人话就是,我们现在有个非终结符,非终结符就是能变出其它东西的东西,一般用大写字母,终结符就是已经不能变了的东西,一般不是大写字母就是。然后我们现在有个句子,我们希望能从开始符出发,然后用给定的产生式捣鼓出给定句子。那LL(1)文法又是个啥呢,就是我现在从开始符出发得到当前这个东西,那既然想推出来,不一样的地方肯定是个非终结符,因为终结符就已经尘埃落定了,不一样就废了,一定要是非终结符,才能通过变身换取一丝余地,而LL(1)文法就是说,我只需要知道一个非终结符和一个终结符就能知道该用哪个式子来变身。所以我们需要先判断是否是LL(1)文法,然后再用得到的变身法则来变身看能不能变出来。
1.剔除多余规则和有害规则
原理说明
-
多余规则
啥是多余规则?没有用的规则就是多余规则!啥是没有用的规则?两种情况!
– 第一种是开始符出发永远到不了的非终结符,这种非终结符的产生式就是无用规则,人家永远都用不着你,备胎都不选你,你在这呆着干啥呢
– 第二种是永远推不出终结符,永远停不了的非终结符。你小子永远终结不了,但是我语法要判断的肯定是一个有限的句子,那要你何用? -
有害规则
有害规则就是,不但帮不上忙,还倒打一耙的规则。通常遇到的有害规则就是A->A这种东西,为啥说它有害呢?因为会有二义性,我们现在想要得到一个句子,根据我们在0中提到的,我希望只需要知道一个非终结符和一个终结符就能知道该用哪个式子来变身,那么如果有了A->A的话,那我既可以选择继续当自己,也可以继续选择变身,因为自己变自己肯定对结果没影响,大不了啥都没改嘛,也可以选择变身,而这就造成了二义性,不能确定选哪一条。
如何做题
直接找开始符一定遇不到的非终结符,以及永远停止不了的非终结符,把这些非终结符的式子直接删了,然后把自己推出自己的全删了(注意,一定是自己出自己,要完全一样,比如A->A才是有害规则,像A->aA这种就不算有害规则了!)
2.提取左公因子(消除回溯)和消除左递归
原理说明
- 啥是回溯?大白话说就是,对于一种情况下有好多种选择,然后你先选择其中一条路,如果走不通了就回来换一条路走。对于LL(1)文法这是不行的,我们想要的是百分百的确定!对于 A − > a b c ∣ a b d A->abc|abd A−>abc∣abd,这种就是左公因子,第一个式子和第二个式子都是ab打头,这样的话就会阻碍我们后面的分析,如果A遇到a,到底是选择这俩式子中的哪个呢?所以需要提取一波,引入一个新的符号A’,那么就变成了 A − > a b A ′ , A ′ − > c ∣ d A->abA',A'->c|d A−>abA′,A′−>c∣d
- 啥是左递归?对于 A − > A b A->Ab A−>Ab,这种就是左递归,这个坏处就是打头的是你自己,但是LL(1)文法其中一个L就是从左到右扫描字符,如果用A->Ab,右边开始变了,从左往右扫描哪里知道右边的情况,所以需要转换。如何转换看下面的如何做题部分吧!
如何做题
提取左公因子:
只用记住公式
A − > a B ∣ a C A->aB|aC A−>aB∣aC这种,引入一个新的非终结符A’,变 A − > a A ′ , A ′ − > B ∣ C A->aA',A'->B|C A−>aA′,A′−>B∣C
消除左递归:
消除左递归要求文法
1.无回路(这个非终结符不能+推导(至少一次推导)出自己)
2.无空产生式(这个非终结符不能推导出空)
- 对于直接左递归
只用记住公式
对于 P → P α 1 ∣ P α 2 ∣ … ∣ P α m ∣ β 1 ∣ β 2 ∣ … ∣ β n P→P α_1|P α_2 |…| Pα_m |β_1| β_2 |…|β_n P→Pα1∣Pα2∣…∣Pαm∣β1∣β2∣…∣βn
要引入新的非终结符P’,变成
P → β 1 P ’ ∣ β 2 P ’ ∣ … ∣ β n P ’ P ’ → α 1 P ’ ∣ α 2 P ’ ∣ … ∣ α m P ’ ∣ ε P→β1P’ |β2 P’|…|βnP’ \\P’ → α_1P’ | α_2 P’|…| α_mP’| ε P→β1P’∣β2P’∣…∣βnP’P’→α1P’∣α2P’∣…∣αmP’∣ε注意这个ε千万别落 - 对于间接左递归
间接左递归就是A能+推导出Ab(类似这种)
比如 S → A a , A → S b ∣ b S → Aa,A → Sb|b S→Aa,A→Sb∣b,将S右部代替A的右部的S,会变出 A → A a b ∣ b A → Aab|b A→Aab∣b,所以这种就是不断的代入,然后用消除直接左递归的方法消除。要注意弄完还得剔除多余规则。
比如:

3.哪些非终结符能推出空
原理说明
能推出空集的就两种情况,一种是本身就有这种产生式,另一种就是推出的某个产生式,右部所有的都是非终结符,而且这些非终结符都能推出空
如何做题
先找到所有能推出空的式子,然后对应的非终结符都能推出空了,然后在其他式子里找有没有这家伙,有的话就删掉,如果某个非终结符能推出的式子都被删光了,那么这家伙也能推出空。
举个栗子
S − > A B A − > ε B − > ε S->AB \\A->ε \\B->ε S−>ABA−>εB−>ε
可见A能推出空,然后把第一条里的A删掉,变 S − > B S->B S−>B,发现B也能推出空,把第一条里的B删掉,发现第一条里的右边都被删光了,那么S也能推出空,就这么一步步下来就行了,可以理解成BFS~每次把被删除的扔到队列里,然后每次取出队首删一波。
4.求FIRST集
原理说明
先说FIRST集是啥,FIRST集就是对于某个非终结符来说,它可能推出的所有可能句子的第一个非终结符或者空。比如说 A − > B c , B − > a ∣ b A->Bc,B->a|b A−>Bc,B−>a∣b,那么A可能推出 A − > a c A->ac A−>ac或 A − > b c A->bc A−>bc,FIRST(A)={a,b}
为啥需要这玩意儿?因为大家想想嗷,我们想要的是知道非终结符和终结符就知道这玩意儿要用哪条式子,现在先要求不那么高,先知道这玩意儿有没有可能推出来,还有的用处在判断是否是LL(1)文法的时候会介绍。所以当我知道了这个非终结符能推出的可能的句子的第一个字符,如果当前句子要推的非终结符不可能出来的话,那就直接game over了,不可能推出这个句子了,否则还有一线希望。同时FIRST集也是我们确定是哪个产生式的利器,这个后面会提到。
如何做题
四种情况(针对每一条生成式):
-
如果遇到了终结符,加入左部非终结符的first集然后停止
-
如果遇到了推不出空的非终结符,将这个非终结符的first集加入左部非终结符的first集然后停止
-
如果遇到了推得出空的非终结符,将这个非终结符的first集除了空以外的元素加入左部非终结符的first集然后继续下一个非终结符
-
如果右边全能推出空,或者直接就是空,那么将空加入左部非终结符的first集
-
注意:由于第二、三种情况中,遇到的非终结符的first集可能还没求完,所以应该反复扫描这些产生式重复以上动作,直到first集不会变动为止
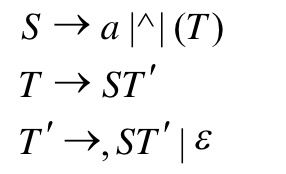
比如对于这个题,先看第一条式子,可以发现a ^ (都是终结符,都符合第一种情况,所以遇到就停,没有其他情况了,所以 f i r s t ( S ) = { a , ^ , ( } first(S)=\{a,\hat{},(\} first(S)={a,^,(},接下来继续看第二条式子!S刚才可以发现,推不出空串,所以就符合第二种情况,将S的first集全部加入T就行,所以 f i r s t ( T ) = { a , ^ , ( } first(T)=\{a,\hat{},(\} first(T)={a,^,(},对于第三条式子,它的第一个式子符合第一种情况得到,,第二个式子符合第四种情况,加入空串,所以就是 f i r s t ( T ′ ) = { , , ε } first(T')=\{,,ε\} first(T′)={,,ε}
第三种情况也很常见,就靠大家自己摸索啦~,比如S->ABCD,ABC都能推出空串,D不能推出空串的话,那就是把ABCD的first集都给S,如果ABCD全能推出空串,那还得在得到所有first集的基础上加入空。
5.求FOLLOW集
原理说明
既然已经有了first集,我已经能知道我能推出啥式子了不就够了嘛,为什么还要来个这个FOLLOW呢?因为非终结符可能推出空!回想我们在第0点说过的目标,我们希望能在知道非终结符和终结符的情况下就能确定哪个式子,但是如果当前非终结符能推出空串的话,那么这个字符有可能不是这个非终结符推出来的,而是它后面的那一坨推出来的,比如S->AB,让你推出的句子是b,然后B->b,假如A的first集没有b,你不能说这个句子拼不出来,因为有可能A主动让贤让B继续顶上,所以FOLLOW集的存在,就是为了这种推出空的情况~那FOLLOW集咋求呢?顾名思义,FOLLOW集就是能直接跟在当前非终结符屁股后面的第一个终结符,所以对于每一个非终结符,要做的就是找到所有包含它的右部,然后把他后面的那部分的FIRST集弄出来,举个栗子,如果S->ABCD,如果想求出B的FOLLOW集,那就找CD的first集。
还有一种情况,如果它后面的部分能推出空,那么它左部的follow集也要加入它的follow集。为啥呢,因为比如S->ABCD,对于B的follow集,如果CD能推出空,那么能跟在S后面的字符同样也能跟在B后头
如何做题
首先开局直接将#放入开始符S的follow集中,这个东西表示句子的结束
接下来两种情况(针对每一个非终结符):
- 找到包含这个非终结符的右部,把这个非终结符右部的first集求出来,比如S->ABCD,对于B来说CD就是它的右部,注意不要加入空
- 如果包含这个非终结符的右部能推出空,那么左部的follow集也加入当前first集
- 注意:由于第二种情况中,左部非终结符的follow集可能还没求完,所以应该反复扫描这些产生式重复以上动作,直到follow集不会变动为止
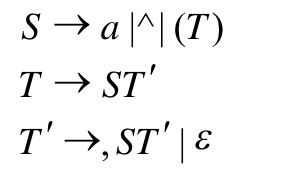
再拿这个做例子
上来直接把#推到S的follow集, f o l l o w ( S ) = { # } follow(S)=\{\#\} follow(S)={#}
对于S,出现它的右部是第2、3条式子,它在这两条式子的右部都是T’,所以刚才我们直接将T’first集弄过来, f i r s t ( T ′ ) = { , , ε } first(T')=\{,,ε\} first(T′)={,,ε},空不要,因为右部能推出空集,所以我们要加入左部T的follow集,发现T的follow集还不知道,所以先待命,目前是 f o l l o w ( S ) = { # , , } follow(S)=\{\#,,\} follow(S)={#,,}
然后对于T,T出现的只有第一条,S->(T),右部是),非终结符的first集就是自己,所以 f o l l o w ( T ) = { ) } follow(T)=\{)\} follow(T)={)}
然后对于T’,T’出现在2 3条,右边都是啥都没有,所以直接加入follow(T)和follow(T’),follow(T’)就是自己,啥都不用动,加入T的follow集就是刚才说的),所以 f o l l o w ( T ′ ) = { ) } follow(T')=\{)\} follow(T′)={)}
待命的S现在可以加入T的follow记集了,然后就会变成 f o l l o w ( S ) = { # , , , ) } follow(S)=\{\#,,,)\} follow(S)={#,,,)}
6.求SELECT集(可以不弄,视你的教材决定)
原理说明
要注意我们需要干的事情是什么,是希望能够知道非终结符和终结符就能确定哪一条式子,而select集的作用就是,比如select(S->A)={a},那么当现在遇到的非终结符是A,终结符是a,就能确定现在要用的式子是S->A,所以select集是针对每一条式子来说,每一条式子的select集首先是右部的first集,如果右部能推出空集,那么很显然左部的follow集也能作为当前非终结符能形成的句子的第一个字符。
如何做题
两步(对于每一条产生式):
- 加入产生式右部的first集
- 如果右部能推出空串,去掉空,然后加入左部的follow集
举个例子,就是如果S->AB,那么就是求出AB的first集,如果AB能推出空(其实就是每个非终结符都能推出空的话),那么就加入S的follow集,就得到了这条产生式的select集
7.判断是不是LL(1)文法
原理说明
再次重申我们需要干的事情是什么,是希望能够知道一个非终结符和一个终结符就能确定哪一条式子。
用select集的方法:
而select集又是得到一个非终结符和一个终结符就能确定式子,所以如果同一个非终结符得到的式子的select集有交集的话,那么它们相遇的时候就不能唯一确定一个式子,变成俩小伙子都行了,出现了二义性。所以我们就只用判断是否同一个非终结符的任意两个式子的select集交集是否为空,如果全为空则是LL(1),否则不是。
不用select集的方法:
LL(1)文法要保证的就是说,一个非终结符和一个终结符就能确定哪一条式子,所以首先对于同一个非终结符,它的所有产生式右部的first集是否有交集,因为如果有交集的话,那么就不能判断到底用哪个式子了。还有一种情况就是,如果它的某一种产生式能推出空,那么就需要判断A的first集和follow集是否交集为空。因为如果A能推出空的话也有两种情况,一种是A不推出空得到的式子,这些式子的第一个字符就是first(A),也有可能推出空,这种情况就是Afollow集的情况, 两者有交叉,就不知道是A选了自己不推空串的产生式继续发光发热, 选择空让位,选自己推出空了,说白了也是避免二义。
如何做题
用select集的方法:
对于相同左部的式子,如果存在任何两个式子的select集交集不为空,就不是LL(1)文法,否则是。
不用select集的方法:
首先判断相同左部的式子,右部的first集是否存在交集。如果某个非终结符能推出空串,那么判断该非终结符的first集和follow集是否存在交集。
如果存在交集,则不是LL(1)文法,否则是。
8.预测分析表
原理说明
这个其实就是写一个表来说明哪个非终结符遇到哪个终结符用哪个式子,如果有select集就方便了,每个式子,左部和select集中的所有元素相遇就说明用这个式子。没有的话,就需要对于每个式子来说,先求出first集,如果这个能推出空,再给这个左部非终结符的follow集-该非终结符的表格相应位置加入这个式子。
如何做题
用select集的方法:
对着select集,表格中非终结符那一栏找到左部对应的非终结符位置,然后在终结符那一栏找到select集里的元素,然后对相应的位置填上这个式子。
不用select集的方法:
对于每个式子,求出右部的first集,然后对左部和first集内的元素相应的位置填上这个式子,如果右部能推出空集,那么在左部的follow集和左部的相应位置填上这个式子。
9.判断句子是否能被接受
原理说明+如何做题
起步就只有一个开始符,然后对照要匹配的句子。然后一个个字符对过来,如果遇到非终结符对终结符,就去预测分析表找对应的式子代进去,然后继续比对。 这里的做题格式就要根据你的课本要求而定啦~
四、结语
如果你能看到这里那我相信你一定已经学会了如何进行自顶向下分析~这篇文章花费了我大量的时间和精力,非常感谢你的陪伴,希望能给你带来帮助~