卷积网络深度和宽度修改（一）

卷积网络深度和宽度修改（一）

盖天地不全，这经原是全全的，今沾破了， 乃是应不全之奥妙也，岂人力 所能与耶! 愿来者补充
随着神经网络的发展，网络的深度逐渐加深（更深的层数以及更小的感受野，能够提高网络分类的准确性(Szegedy et al.,2014;Simonyan & Zisserman,2014)），网络的训练也就变得越来越困难。训练越来越难的原因是由于深度加深会出现梯度消失的问题。首先来说明一下梯度消失的问题。

一，梯度消失/梯度爆炸的问题

这是被说的很多的问题，这里就简单介绍一下。对于激活函数我们一般会使用sigmoid函数，和tanh函数，还有最近用的比较多的RELU函数，我先介绍前面2个经典的函数。

上图是sigmoid函数，这个函数会吧数据压缩到（0，1）范围内，0 就不通过，1代表全都通过。

这是tanh函数，可以把数据压缩到(-1，1)之间。
我们观察上述2种函数可以发现，函数的导数是处处可导，但是导数值会出现不同的值，比如sigmoid函数，只有在x=0出导数才等于1，其他地方都小于1。
上面说的内容已经明白了，我们开始说为什么会出现梯度消失/梯度爆炸的问题，神经网络训练的方法用的是BP算法，最基本的就是链式求导法则，简单来说就是会有导数连乘，看sigmoid和tanh函数，由于导数不是都是1，如果小于1，backword时候经过多个连乘传到浅层时，梯度会很小很小，这就是梯度消失，一旦梯度消失浅层网络就学习不到新的特征了;如果大于1，经过k个乘法后会变得异常巨大，毕竟是指数级的，这就是梯度爆炸了，会导致网络权值更新不稳定。
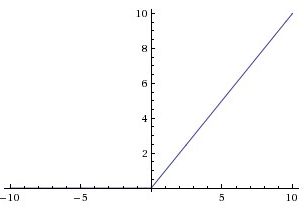
出现上述问题我们很自然的想到，如果激活函数的导数是都是1呢是不是可以解决以上问题。这函数是存在，如RELU，如下图可以看出导数始终为1，这个问题，在后面部分会进行补充说明，介绍完梯度消失/梯度爆炸的问题，还是直接说明主题。

二，通过调整网络结构来加深网络深度

Highway Networks

这篇算是很经典的一篇文章了，现在很火的ResNet也是受这个启发.
一种可学习的门限机制，在此机制下，一些信息流没有衰减的通过一些网络层，适用于SGD法。

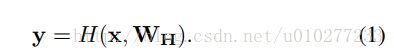
H为非线性函数，W权重，x输入，y输出。

这里作者设计了这么一个非线性变换，T（x，W）和C（x,W）.T as the transform gate and C as the carry gate,暂且翻译成转换门和携带门，这样y不仅依赖于对输入转化的结果也依赖于输入本身。

为了简化公式（2），设置C=1-T即得公式（3）。x, y, H(x,WH) and T(x,WT) must be the same for Equation (3) to be valid. 这4个矩阵的维数必须相同不同就补0。

特别的，T=0 和T=1的时候入公式（4）。

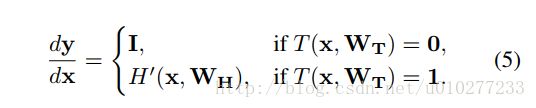
同样的对于导数来说，就如公式（5）。


对于第i层的输出来说，就如公式（6）。
论文写的很清晰，也很容易懂，回到刚开始的那就话，一种可学习的门限机制，在此机制下，一些信息流没有衰减的通过一些网络层，适用于SGD法。是不是顿时清晰了许多。

Highway Networks的思想呢。来自于LSTM。那么提到LSTM就不得不提RNN了。对于这2个我就不过多的说明了，毕竟不是我要说的重点，想了解来看这里还有这里.

Residual Network

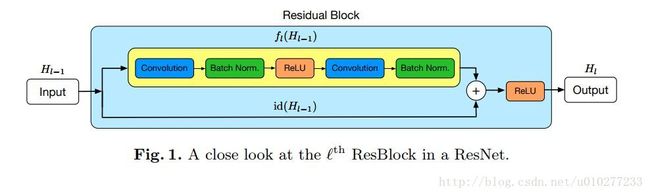
ResNet的结构与Highway很类似，如果把Highway的网络变形会得到，而在ResNet中，把 transform gate设置成0.5，就得到一个残差函数F(x)=H(x)+x，而且会得到一个恒等的映射 x ，这叫残差网络，它解决的问题与Highway一样，都是网络加深导致的训练困难和精度下降的问题。残差网络的一个block如下：

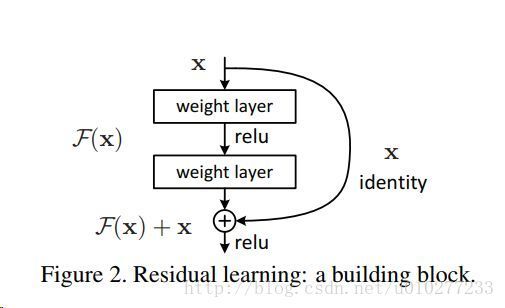
residual block 其实就是 transform function T 为两个卷积和一个relu, transform gate是一个data independent 值为0.5 的一个 highway layer，残差只是的换了种说法，虽然说是换了个说法，但是不得不佩服kaiming大神的解释和设计的相关实验。文章提出假设：加入的后续层如果都能够做到将前一层的结果直接map到下一层的话，那么该加深后的网络理论上是保持一样的误差而不是增大训练误差了。那么也就说明现有的求解器solvers在我们构造出来的更深网络上并不能找到更好的解。那么我是不是可以引入残差（在很多领域应用到过）的概念，让该求解器能够稳定下来更容易收敛呢？答案是肯定的，文章在多个数据集上验证了自己的想法。
下面这个摘自
Deep Residual Network 那篇工作，讲到，自己比 Highway Networks 的一个优势是，parameter 少，并且自己的“gate”永远不 close。这两个优势，既都对，也都不对。关于第一点，这是事实，而这恰恰是把 Highway Networks 的一个优势给抹掉了。在 Highway Networks 文章的 4.1 部分，有讨论自己这种 adaptive mechansim for information flow learning 的优点。也就是说，如果说 Highway Networks 是 data-independent 的，那么 Deep Residual Network 就是 data-dependent 的，不 flexible，更可能不“最优”（Deep Residual Network 就是 Highway Networks 中提到的 hard-wired shortcut connections），它只是一种 p=0.5 的二项分布的期望（np）。关于第二点，就不一定是事实了。因为实际上，虽然公式（3）看起来，transform gate 有可能完全 close，然而 transform function 却永远不可能为 0 或者 1，它的取值范围只是 (0,1) 开区间，所以在这点上它和 Deep Residual Network 是一样的。

Deep Networks with Stochastic Depth

这篇文章是在Residual Network基础上进行了改进。直接用公式说明。

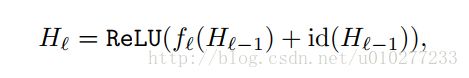
这是原始的ResNET，对应的网络如下图。

作者的改进就如公式(2)，看就是加了一个

bl

参数,取值为0（active）或者1（inactive），为了确定b的值，引入p（survival probability），

pl=Pr(bl=1)

p的取值如下图。

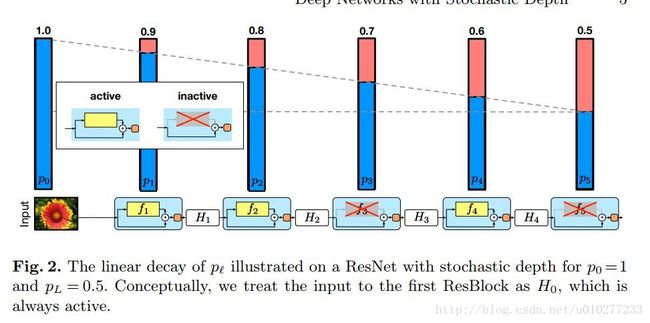
这篇文章的想法很简单，从上面的图和公式就可以看出来就是随机的让深度减少，来制造不同的深度。该加深网络方法的缺点是：虽然减少了训练的时间，因为自身在训练的过程中随机的去掉一些层，但是在测试的时候是会使用完整的网络但确不能减少前向的时间。不过它是一个非常有效的类似于dropout、drop connection的regularization的方法，能有效采用这样的加深网络的方式来提升模型性能。

FractalNet:Ultra-Deep Neural Networks without Residuals

FractalNet 利用分形的结构来设计神经网络，效果可以匹敌ResNet. 但是引用量来说差的不是一丢丢。但是思路还很好的，所以还是来介绍一下。看起来也是很简单的。

这个主要的结构图了。图结合公式来说，先看公式

f1(z)=conv(z)

fC+1(z)=[(fC∗fC)(z)]⊕[conv(z)]

这是个递推公式，主要的都有一个个 fc 这样的小单元构成的，其中*表示其中的构成，就是图中红色的conv层接conv层，⊕表示连接的操作，就是图中的绿色的层。其中的 C 原文中说是, C corresponds to the number of columns, or width, of network fC(.) . Depth, defined to be the number of conv layers on the longest path between input and output, scales as。 2C−1 .解释起来很简单就是C代表第C“层”，这里的“层”指的是pooling层（图中的黄色部分）到下一个pooling层为一层，那么第C“层的最长的卷积路径有 2C−1 个卷积层，看图中的最右边我们就能对应上了，C=4， f4(z) 就最长有2^3=8个卷积层，就是最右边的一列了。

此外，看下图，作者特意为了和ResNet区别开，还做实验并说明了原因。

1，简单来说就是FractalNet中对待所有层的输出信号是一样的，没有区别，但是ResNet中是有区别的对待了网络传递过来的信号和残差信号。
2,3点讲的都是一个东西了，都会Drop-path实验中说明了。
下面说一下Drop-path，然后在说回区别。

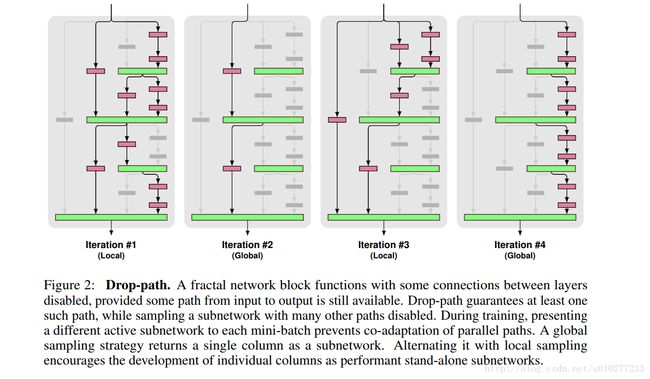
学习Dropot和drop-connect改变网络的，作者就设置了Drop-path，毕竟论文中提出的网络的宽度很宽就会有许多条路径可以选择。由于有很多种选择路径的方法，作者考虑了2中，一种叫Local，看上图左一Iteration #1(Local)和右二Iteration #3，每层有一个固定概率可以传递到连接处，但是要保证至少有一条路；另一种叫Global，看上图左二Iteration #2(Global)和右一Iteration #4就选一条通路，这样可以保证单列也很强的独立预测能力。
经过试验，发现使用global drop-path这样的方式，可以产生很多种不同的子网络，这些子网络表现出整个大网络的多样性，就这个属性来说，ResNet中只是随机深度（即会有一定概率丢掉一些网络），是很多子网络的在深度上集中而成的。个人意见呢，觉得这么说是很自然的，毕竟FractalNet的宽度宽呀，当然可以有很多种选择了，ResNet的的只是在深度上进行了加深。
我觉得这网络给的最大的启发就是宽度可以加宽，使用drop path来进行训练。

Identity Mappings in Deep Residual Networks

该文章主要对原文ResNet的残差单元做了两方面做了详尽的实验,当然还是凯明大神写的咯：1. shortcut类型 2. 激活函数顺序。就可以对原始结构做一些优化，shortcut类型的实验如下：

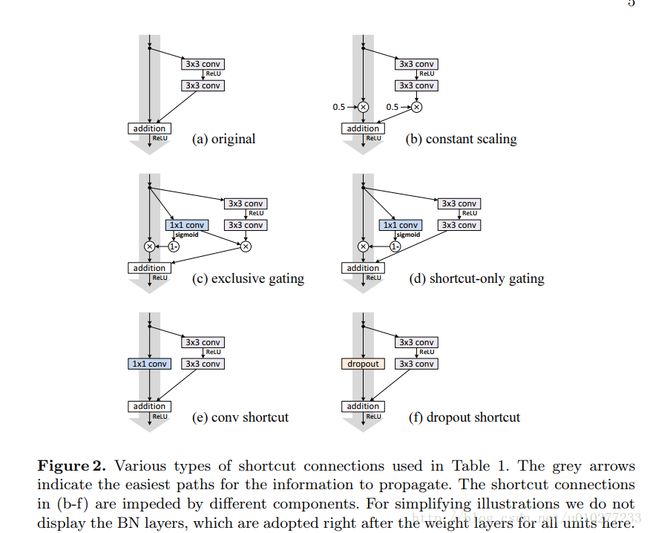
结果证明第一种原始的最好。
激活函数顺序实验如下。

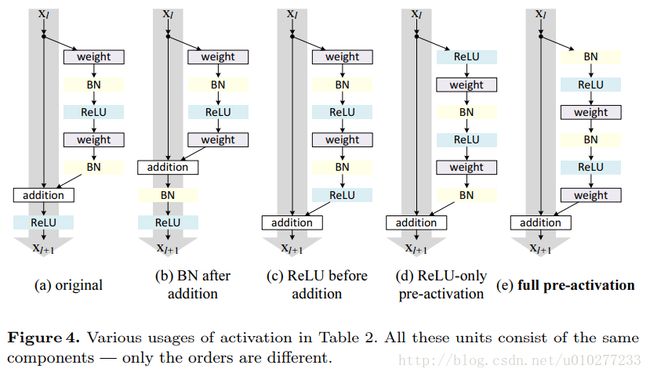
证明是最后一种好，将激活函数都放在weight之前。
其他细节包括数学推导和各种数据分析和说明部分，可以去看论文，佩服凯明大神做的试验和解释。结论就是作者可以生成1000层的Net也能够很容易训练和获得很好的正确率。个人觉得就是论证了一些在ResNet中未试的结构，还有就进一步说明和解释了ResNet设计的结构是对的，很不错。

RESNET IN RESNET:GENERALIZING RESIDUAL ARCHITECTURES

文章中提出了ResNet的一种补充吧RESNET IN RESNET（RiR），老规矩先上图。

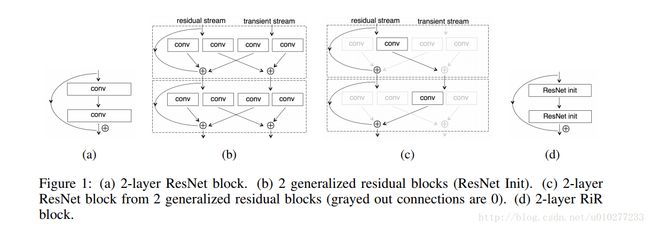
图中（a）就是原始的ResNet中Block,(b)是本文提出的方案，首先大的方面来说这个block分为residual stream(称为r)和transient stream（称为t），r中具有identity shortcut而t中没有， r和t计算的公式，我用下图直接说明，就无需我用过多的语言解释了。

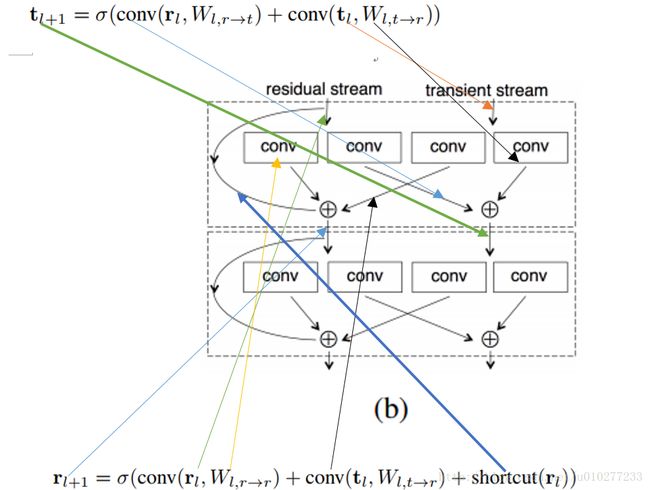
图一中的（c）是来说明（b）中设计的结构是包含ResNet的结构的。(d)是将（b）进行广义化，说实话这转换要是作者不解释还真不好理解，幸好作者在后面进行说明。还是图和公式看的清楚，先看公式（2）。

这里讲 [rltl] 记为 xl 那么之前复杂的的 rl+1 和 rl ， tl+1 和 tl 之间的转化就简化为公式（2）中 xl+1 和 xl 之间的转化。就可以看出一层了，作者记为ResNet Init，所以才有了图一种（b）到（d）的广义化。作者之所以这么设计这么一个block的原因在于很多特征是不需要传到后面的层的，所以就是阻止了identity shortcut中一些底层的特征进行流动。个人觉得由于宽度的增加也会导致结果变好，所以效果感觉是2方面的原因造成的。

Residual Networks are Exponential Ensembles of Relatively Shallow Networks

这篇文章提出一个新的观点：残差网络并不是一个真正意义上极深的网络，而是隐式地由指数个大部分为浅层网络叠加而成的。还提出multiplicity来论证。所以怎么解决很深的网络中梯度消失还是个问题。

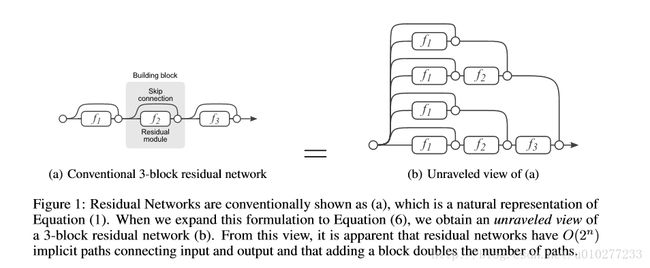
图一中的（a）就是ResNet中的3个block，那么通过分析作者将（a）拆分为（b），可以看到下图中的公式（4）就是图一中（a）的结果，经过替换和变化就变成公式（6）（即图一中（b））。相信这点是毋庸置疑的。从图一（b）来看，那么ResNet就有 O(2n) （就是multiplicity）这么多条路径连接着input和output，因为每个block都有2条路可以选择，但是一个普通的网络比如VGG结果那么multiplicity就是1，因为从输入到输出就是一条路（看图二的（b））。

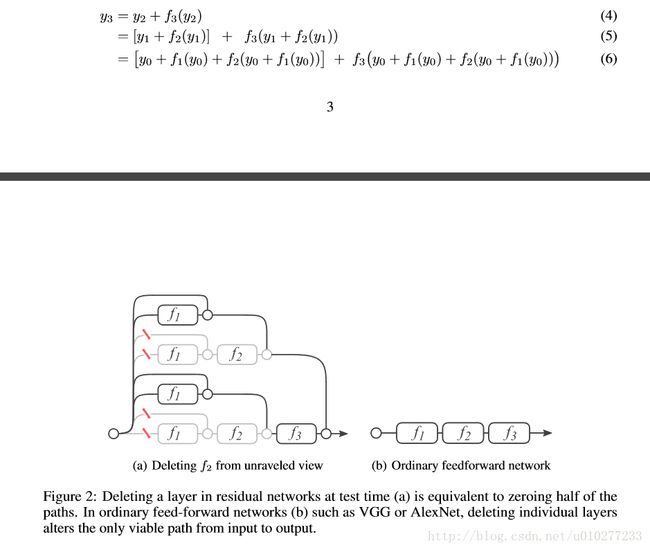
为了论证ResNet是很多浅层网络叠加而成的，作者做了一个Lesion study。首先按照reNet的训练过程进行训练，在测试的时候回进行一些操作。
一：删除一些独立的层，证明ResNet中不是所有的操作都是必须的。具体如下公式：
yi=yi−1+fi(yi−1)toy′i=yi−1
即删掉了一些block，结果证明即使删掉了一下对结果的影响还是很小的，而VGG删掉中间的效果直线下降了，这很自然能想到，VGG你删掉中间学习到的特征当然结果就不对了，但是对于ResNet删掉了效果差不多，就说明ResNet中有很多子网络，这些子网络有能力学习到了足够的特征，所以删掉一些还是可以工作的这样就说明了ResNet是很多浅层网络组合成的。
二：删掉很多ResNet中很多模块。
随着删除的ResNet block越来越多，错误也是很平滑的增长。看图五（a）就很明显了。

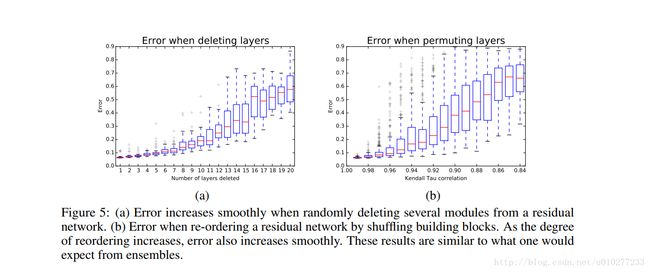
这里的实验来论证了侧面反映了ResNet是很多浅层网络组合成的。
假设ResNet是很多浅层网络组组成的。
由于组合成的网络有个特点，预测的结果和子网络的数目是平滑相关的，组合的子网络越多那么效果越好，反之越差，这点也是很自然的可以想到，子网络越多学习到的特征越多那么就越接近真实的情况，也能应对各种输入。所以作者就随机的删除了ResNet block来论证了上面的假设。
三：前面2个实验都是删除一些结构，这个实验是重新排序ResNet block。听起来很有意思。
作者moves high-level transformations before low-level transformations.还是原文的话好理解，简单来说就是把高层的block移到了低层。结果呢可以看图五（b），随着打乱的越来越多，错误率也是平滑的增加的，没有突变，要是VGG估计就是突变了。但是对于ResNet这样的结果也是很意外的，毕竟结构都已经变了。但是这也暗示了ResNet是共享了特征，通过很多浅层网络。这里共享特征很好理解，就是高层的和低层的共享了一部分的特征，但是为什么说是通过很多浅层网络呢。这点其实作者并没有怎么解释，我个人解释是，若不是很多浅层网络的话，很难做到低层和高层网络共享特征，思考一下一个第5层的特征跑到第95层去共享的概率是多大，我们假设每次有1/2的特征传到下一层，那么从第5层到第95层共享的特征只剩 1/290=8.08∗e−28 很小很小的一个数了，那么在这种情况下就不可能会得到图五（b）中平滑的曲线了，既然得到了，那就说明低层的特征其实并没有传多远，那么就说明了 high-level transformations只不过是很多浅层网络的 high-level high-level transformations。所以一个ResNet看起来是很深，其实是很多浅层网络叠加，共享特征。
个人观点：It is not depth, but the ensemble that makes residual networks strong. 作者在conclusion用加粗字体来提醒，可是ResNet实在是有效好用，这个点大家关注的也就少了所以引用量也少。不过这也是作者的一种分析，实际上到底是不是这样其实还不好说，只能说提供了一个新的思路吧。可以给大家一个新的研究方向了。但是通过作者的分析，我们按这个思路来分析一下之前的改进，其实我们可以发现都是让浅层网络更多，共享的更多，这样效果更好了，那么更深的网络问题还是没有解决。从这点来看，目前的解决思路或者研究方向是有以下：
一是大混合，就是各种混合呀各种操作呀，为的就是共享特征，学习很多浅层网络，就好像一个浅层网络学习一种特征一样特性，很多种特性并行加起来那么效果就好了，不想以前的串行，所以很容易会overfitting。这个还可以研究下去就是不同的混合嘛，但是这方面的研究呢，毕竟ResNet的效果摆在哪里，你想做也不会好过ResNet了。
二：就是真的做到深度网络，很深的网络也能解决梯度问题，这方面可能你做出来，但是最终大家看到的是效果，可能效果还是不如ResNet或者说没有好很多。
三：我觉得可以做的就是实现了第二点的基础上，让宽度更宽，就相当于，很多个深层网络叠加的效果，肯定是比现在浅层网络叠加好，但是训练的难度也会成为一个问题，这点我暂时没有考虑啦，哈哈。要是效果好，训练快，那就是最棒的了。
当然了对于这方面的研究还有很多，先码到这里，还有一些有特点的，还有之前未说明的问题如RELU，在后面的会继续补充。

参考链接：
http://www.cnblogs.com/jie-dcai/p/5803220.html
http://blog.csdn.net/l494926429/article/details/51737883
https://mp.weixin.qq.com/s?__biz=MzAwMjM3MTc5OA==&mid=402156285&idx=1&sn=13275b8f4ec46c901290c66c6c0ffa28
https://www.zhihu.com/question/38398005
https://zhuanlan.zhihu.com/p/22447440
http://blog.csdn.net/sunbaigui/article/details/51702563
http://baijiahao.baidu.com/s?id=1575180693817721&wfr=spider&for=pc