编译原理:LL1算法
但凡有一点良知的人,既然干了,那就把它干好。
网上搜索的大部分文章要不写的晦涩难懂,要不就是太简单,甚至经不过考试的检验。
你花了更多的时间,将这个事情全部说清楚了,别人看了就会大大节约时间。而不是当初这个东西老师填在你脑子里,然后你也短时间理解了,但那只是你嚼过的膜,不一定适合别人。
我想把这个坑填上,留给后人,让他们能在很短的时间了解事情的全貌。
LL1的通俗理解
我在设计一个编译器的语法分析阶段,我才会用LL1算法。
它是一种自上往下的分析算法。
各位不必深究自上而下这个概念,实际上这个概念甚至来说就是一句话。从上往下进行扫描。
编译器拿到了Token序列,开始来到语法分析阶段。它需要搞清楚一件事,语法分析是干啥的?
语法分析就是用来分析你写的if()else(){}这个串(当然词法分析送过来的是Token序列)符不符合你所定义的语言。(由文法来评判)
Oh~怎么进行判断。当然不是傻瓜似的通过暴力破解型的进行一个个的试,走不通进行回溯。
相反,编译器的作者设计了两种思路。–从上到下,和从下到上。我直接告诉你,从下到上效果更好,当然也更难。
很不幸,我们现在说的LL1算法是属于从上到下,属于那种吃力不讨好的类型。
既然吃力不讨好,经过我多年的经验,那就一定会有一堆仁人志士开创属于这个玩意儿的奇技淫巧。我们普通人不要创新,就会用就可以了。
输入:set
文法:
S->N V N
N->s
|t
|g
|w
V->e
|d
现在就是怎么判断set是不是属于这个语言。
好吧,现在如果我们知道了输入s的话,N里面到底有没有s,是不是就不用回溯了?
ok。让我们来构造这样一个 预测分析表。
可是,emmm,怎么做啊?
插一嘴:消除左递归&&提取左公因子
这一步是必要的。非常必要。它关系到
该文法能不能用LL1算法。(LL1实在是有些繁琐)
左递归
想到左递归,就会想到这个公式:
βααααααααα…(这个式子左递归吧)
于是不禁好奇原式子是什么?怎么构造"左"递归?
A->Aα|β
说实话,其实如果是下工夫想过这个问题,对这个式子为什么这样写应该很清楚。
我不能左递归。(为什么?举个例子:E->ET,E->ET.E->ETT,E->ETTT…)
但我还想保持式子还是那个样子。
我可以这样做:
A->βA'
A'->αA'|ε
还有直接左递归.间接左递归.
上面是前者。后者举个例子:
S -> Aa | b
A -> Sd | ε
解体思路:
A里面有S,S里面有A。不太直接。想办法变成直接。
A->Aad | bd | ε
> 消除直接左递归
A->bdA'
A'->adA'|ε
总结:
S -> Aa | b
A->bdA'
A'->adA'|ε
左因子
在扫描到下面的串的时候,如何进行选择,是不是非常棘手?
S->aBcD|aCE
消除左因子说的思想就是我先不急着选择,因为还有相同的部分。
我把相同的部分给提取一下,这样扫描到a的时候就不急与做选择。
也许a的下一个很好判断呢?
解决方案:
S->aS'
S'->BcD|CE
first集和follow集不能相交
first集 ∩ follow集 != Ø
下一步怎么做?
这就是我说的那个很emmm,你不用瞎操心的问题。
别人说了这么搞,那我们就跟着这么搞。
下面给出步骤:
1.会填first集
2.会填follow集
3.会填预测分析表
你会惊讶的发现,如果你把问题分解成如此微小的问题后,事情变得开始有趣起来了。
First集怎么填
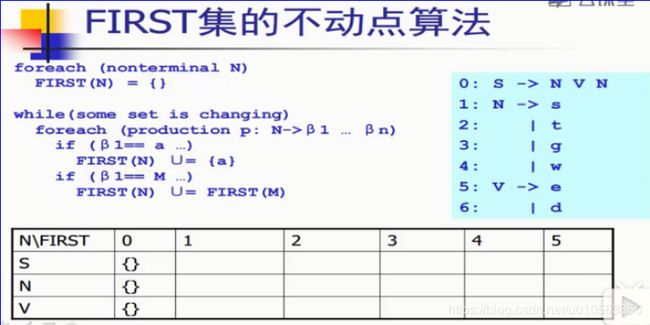
这个就是公式了,原封不动的搬过来。
下面就是以上面那个例子,来进行填写。
为了和算法没有出入,这里不采用编译原理的
方言,给出最标准的求First集的算法。
—所谓算法,就是人知道程序该怎么做。
S->N V N
N->s
|t
|g
|w
V->e
|d
首先先填最简单的终结符
| First集 | … |
|---|---|
| s | {s} |
| t | {t} |
| g | {g} |
| w | {w} |
| e | {e} |
| d | {d} |
然后我们将填非终结符的first集。非常小心的填写。
first集的填写是一个迭代的过程。它不是说一下子我就填出来了。不是这样的。它一定是经过若干轮填写后得出的。我得填写一遍又一遍。这样虽然笨,但聪明的人可能不会想到,这样是最行之有效的一种做法。如果把我们填写的过程看成是一种计算,那以计算机之效率,这做法还是很香的。
| First集 | 第1轮 | 第1轮(整理) |
|---|---|---|
| … | … | … |
| S | {}(原本集合S)∪{} (S后面是N,N的first集还是{}) | {} |
| N | {}∪{s}∪{t}∪{g}∪{w} | {s,t,g,w} |
| V | {}∪{e}∪{d} | {e,d} |
好的,看到了,整理后的集合和原集合比肯定是扩散了,我们要等到集合收敛才结束我们的算法。
这是第1轮计算first集。
| First集 | 第1轮 | 第1轮(整理) | 第2轮 | 第2轮(整理) |
|---|---|---|---|---|
| … | … | … | … | … |
| S | {}∪{} | {} | {}∪{s,t,g,w} | {s,t,g,w} |
| N | {}∪{s}∪{t}∪{g}∪{w} | {s,t,g,w} | {s,t,g,w}∪{s}∪{t}∪{g}∪{w} | {s,t,g,w} |
| V | {}∪{e}∪{d} | {e,d} | {e,d}∪{e}∪{d} | {e,d} |
还没完,还在扩散。我们进行第3轮。
| First集 | 第2轮 | 第2轮(整理) | 第3轮 | 第3轮(整理) |
|---|---|---|---|---|
| … | … | … | … | … |
| S | {}∪{s,t,g,w} | {s,t,g,w} | {s,t,g,w}∪{s,t,g,w} | {s,t,g,w} |
| N | {s,t,g,w}∪{s}∪{t}∪{g}∪{w} | {s,t,g,w} | {s,t,g,w}∪{s}∪{t}∪{g}∪{w} | {s,t,g,w} |
| V | {e,d}∪{e}∪{d} | {e,d} | {e,d}∪{e}∪{d} | {e,d} |
我们发现,第3轮和第2轮竟然完全一样。现在我们可以放心的说我们找到first集了。
上面这个例子没有ε,对吧。下面给一个有ε的。
S->aABe
A->bA'
A'->bcA'|ε
B->d
| First | 1’ | 1 | 2’ | 2 |
|---|---|---|---|---|
| a | {}∪{a} | {a} | … | … |
| e | {}∪{e} | {e} | … | … |
| b | {}∪{b} | {b} | … | … |
| c | {}∪{c} | {c} | … | … |
| d | {}∪{d} | {d} | … | … |
| S | {}∪{a} | {a} | {a}∪{a} | {a} |
| A | {}∪{b} | {b} | {b}∪{b} | {b} |
| A’ | {}∪{b}∪{ε} | {b,ε} | {b,ε}∪{b}∪{ε} | {b,ε} |
| B | {}∪{d} | {d} | {d}∪{d} | {d} |
Follow集怎么填
follow集的算法不用看了,看不懂的。我们直接把算法描述一下才可以继续进行。
follow集的约定:
- 只有
非终结符 - 没有
ε
我以一个例子来说明这个算法。
S->aABe
A->bA'
A'->bcA'|ε
B->d
first集:
| first | 1’ | 1 | 2’ | 2 |
|---|---|---|---|---|
| S | {}∪{a} | {a} | {a}∪{a} | {a} |
| A | {}∪{b} | {b} | {b}∪{b} | {b} |
| A’ | {}∪{b}∪{ε} | {b,ε} | {b,ε}∪{b}∪{ε} | {b,ε} |
| B | {}∪{d} | {d} | {d}∪{d} | {d} |
这个例子中,我们来求S,A,A',B的follow集。
对于S来说,它是开始符号。也是我们求follow集的
入口。也就是我们必须先求follow(S)。
follow(S)=#
#是约定
对于A来说,我们看它出现在产生式的右部。发现
S->aABe有它的身影。那么,我就直接说吧。如果B!=空,那么follow(A)=first(B)。
如果B==空呢?
follow(A)=first(B)∪follow(S)-{epsilon}
follow(A)=first(B)={d}
对于A’来说,
A->bA'似乎是它的归宿。
这种情况十分简单粗暴。
follow(A')=follow(A)={d}
对B来说,就十分正常了。按照这个文法:
S->aABe
follow(B)={e}
down!
predict集怎么填
预测集。对
产生式进行预测。
| first | 1’ | 1 | 2’ | 2 | 3’ | 3 |
|---|---|---|---|---|---|---|
| E | {}∪{} | {} | {}∪{} | {} | {}∪{id,(} | {id,(} |
| E’ | {}∪{+}∪{ε} | {+,ε} | {+,ε}∪{+}∪{ε} | {+,ε} | — | {+,ε} |
| T | {}∪{} | {} | {}∪{id,(} | {id,(} | — | {id,(} |
| T’ | {}∪{*}∪{ε} | {*,ε} | {,ε}∪{}∪{ε} | {*,ε} | — | {*,ε} |
| F | {}∪{id}∪{(} | {id,(} | {id,(}∪{id}∪{(} | {id,(} | — | {id,(} |
follow集:
follow(E)={#,)}
follow(T)=first(E')={+}∪follow(E')={+,#,)}
follow(E')=follow(E)={#,)}
follow(F)=first(T')={*}∪follow(T)={+,#,),*}
follow(T')=follow(T)={+,#,)}
现在整理一下:
文法:
(1)E->TE’
(2)E’->+TE’|ε
(3)T->FT’
(4)T’->*FT’|ε
(5)F->id|(E)
First(E)={id,(}
First(E')={+,ε}
First(T)={id,(}
First(T')={*,ε}
First(F)={id,(}
follow(E)={#,)}
follow(T)={+,#,)}
follow(E')={#,)}
follow(F)={+,#,),*}
follow(T')={+,#,)}
Predict(1)={id,(}
Predict(2)={+,#,)}
Predict(3)={id,(}
Predict(4)={*,+,#,)}
Predict(5)={id,(}

网上讲的这个是把它分开了。分而治之。。。我这个是把它合起来了。就是有的S->A S->b的我把它写成S->A|b了。暂时不清楚这样写对不对,不过把它合起来也是我的答案。
LL1分析表
给出一个例子:
(1)S->aABe
(2)A->bA'
(3)A'->bcA'|ε
(4)B->d
first(S)={a}
first(A)={b}
first(A')={b,ε}
first(B)={d}
follow(S)={#}
follow(A)={d}
follow(A')={d}
follow(B)={e}
predict(1)={a}
predict(2)={b}
predict(3)={b,d}
predict(4)={d}
LL1分析表满足一下几个特征:
- 左边是非终结符
- 上面是终结符
- 填写的内容是产生式
- 根据预测集填写
| a | b | c | d | e | # | |
|---|---|---|---|---|---|---|
| S | aABe | |||||
| A | bA’ | |||||
| A’ | bcA’ | ε | ||||
| B | d |
ok! done.
下一步是根据预测分析表来进行语法分析。
输入:abcde
分析:
abcde
a b
A A A' A'
B B B B
S e e e e
# # # # #
1 2 3 4 5
--
输入:
1:abcde
2:abcde
3:bcde
4:bcde
5:cde error
输入:abcce
分析:
abcce
a b
A A' A'
B B B
S e e e
# # # #
1 2 3 4
--
输入:
1:abcce 展开
2:abcce 匹配a
3:bcce 按照A->bA'展开
4:cce error

