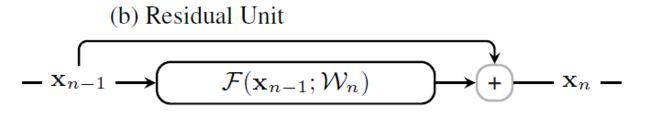语义分割--(FRRN)Full-Resolution Residual Networks for Semantic Segmentation in Street Scenes
FRRN
Full-Resolution Residual Networks for Semantic Segmentation in Street Scenes
收录:CVPR2017(IEEE Conference on Computer Vision and Pattern Recognition)
原文地址:FRRN
代码:
- 官方:Theano
- TensorFlow
Abstract
语义分割广泛应用于多个领域,现阶段先进的语义分割模型大多依赖于预训练的网络,这些网络有着出色的识别性能(即语义特征丰富),但缺乏定位精度。
为了缓解这个问题,论文提出了一个新颖的类似于ResNet的网络架构,使用两条处理流将多尺度上下文信息和像素级精度结合起来:
- 一条流以全分辨率携带信息,用于实现精准的分割边界
- 另一条流经过一连串的池化操作获取high-level的feature用于识别。
两条流使用FRRNs单元做耦合。在没有额外的后端处理和预训练的情况下,模型在CityScapes上达到了71.8%mIoU.
Introduction
现如今自动驾驶是一个热门话题。自动驾驶内的一个重要的部分是理解驾驶周围环境。语义分割实现了各类目标之间的精确分割,可作为自动驾驶的前端处理帮助识别目标和目标关系。在本文中,我们追求高质量的、边界分割精准的语义分割系统。
当前先进的语义分割系统都大多采用某种形式的FCN结构,即采用图片作为输入,以每个类别概率图作为输出。许多方案依赖于在分类任务上(ImageNet)预训练的网络,例如多种VGG和ResNet变体。预训练能够帮助模型预先设置模型权重,与只使用目标数据从头开始训练相比,减少了训练时间且常有更好的性能。然而使用预训练的模型有一个固有的限制,即已存在的预训练网络结构无法改变,这限制了新方法的设计,例如难以添加BN层或新的激活函数。
语义分割系统使用FCN架构时,常见的策略是使用池化或下采样操作降低feature的空间分辨率以获取high-level features,这么做有两个原因:
- 可以显著的增加接受野
- 让模型鲁棒性更强,能够应对小的图片变换(即内在不变性)
池化操作能够高度描述图片中物体,但是这对定位精度会造成巨大的损耗(池化丢失大量的空间信息)。许多工作想克服这个问题获得精确的分割结果。例如Deconvolution-Conv、Dilated等等
本文提出了一个新颖的网络架构,整体采用encoder-decoder架构,基本单元和残差单元类似, 不需要额外的后续处理或者预训练模型。新的架构使用两条流:
- 一条流是(池化流–>语义流):进过一连串的池化操作,用于捕捉图片中的语义信息
- 另一条流(残差流–>细节流):携带全分辨率的特征,用于提供精准的边界信息
新的架构示意图如下所示:
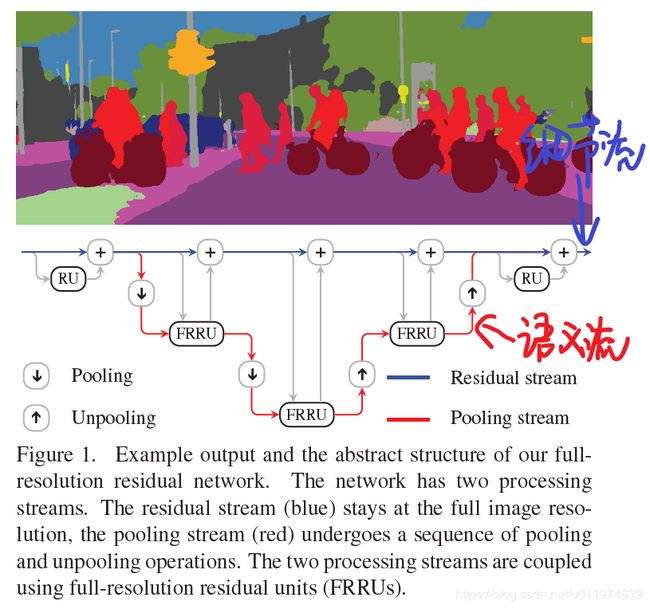
两条流通过全分辨率残差单元(FRRU)相结合,最后得到预测结果上采样到指定大小。
论文的主要贡献在于:
- 提出了一种新颖的网络架构,适用于精准的街道场景,不需要预训练的情况下在CityScapes上达到state-of-the-art水准
- 论文使用两条流结合实现了目标的识别和定位。一条流经过一连串池化操作获得语义信息,另一条流以全分辨率通过提供细节信息
- 公开了代码(Theano实现的…)
Related Work
深度网络在语义分割任务上表现不凡,对于深度网络的训练需要大量标准数据集。近期有发布了许多高质量的数据集以鼓励进一步探究新的分割系统,如Synthia、KITTI和CityScapes。论文选用的是CityScapes。考虑到深度学习对语义分割系统性能巨大提升,论文将review相关工作限定在基于深度学习的语义分割系统和深度网络架构。
Semantic Segmentation Approaches:
过去几年内,大多数先进的语义分割系统都是基于CNN。其中,较为出名的是使用end-2-end训练的FCN架构,该工作将预训练网络调整用于语义分割,获得了显著的性能提升。
在FCN中使用连续的池化操作,用于扩张feature的接受野并提升分类性能。但同时会显著降低feature空间分辨率,导致丢失空间细节。为了克服这个问题,有使用skip connection扩展feature;有使用encoder-decoder结构的,encoder提取语义,decoder恢复空间细节。与这些方案不同的是,论文通过一条单独的高分辨率数据流携带全分辨率信息传入整个网络。
也有许多方案对CNN的输出作平滑操作用于提升预测结果。常见的如DeepLab系列使用的CRF,也有将CRF化为平均场结合整个模型实现end-2-end训练。一些工作使用域变换或超分辨率平滑结果。本论文的方案能够快速的结合低分辨率和高分辨率的特征。实验证明添加额外的CRF平滑对性能没有显著的提升。
Network Architecture:
自从AlexNet在ImageNet上大放光彩,视觉领域迎来了几个里程碑性的CNN架构。VGG使用小卷积核堆叠,GoogleNet使用BN层。最近大多数网络以ResNet架构为基础,这些方法与早期的相比有巨大的性能提升,展现出模型架构的重要性。然而这些工作都是面向分类任务设计的,许多情况下都是在ImageNet上做了预训练,这对语义分割这样的像素级任务来说,会有一些设计上的选择导致非最优性能。本论文的方案是针对语义分割任务提出的,在CityScapes上达到有竞争力表现,且不需要做预训练。
Architecture
Feed-Forward Networks
大多数前馈网络(例如VGG),都是由一系列的线性层组合而成。网络中每层的计算记为 F F F,对于 n n n-th层网络输出记为 x n x_n xn:
x n = F ( x n − 1 , W m ) x_n=F(x_{n-1},W_m) xn=F(xn−1,Wm)
其中 W n W_n Wn是该层的参数,论文称这样的网络为traditional feedforward networks.
traditional feedforward networks示意图如下:
Residual Networks (ResNets)
残差网络在ResNet解读详细讲过。残差网络允许使用更深的网络训练。ResNet由一连串的残差单元(residual unit,RU)组成。对于 n n n-th层网络输出记为 x n x_n xn:
x n = x n − 1 + F ( x n − 1 , W m ) x_n=x_{n-1}+F(x_{n-1},W_m) xn=xn−1+F(xn−1,Wm)
其中 F ( x n − 1 , W m ) F(x_{n-1},W_m) F(xn−1,Wm)是残差,参数是 W n W_n Wn。残差网络不直接学习 x n x_n xn,而是学习残差 x n − 1 x_{n-1} xn−1.
从经验上看,ResNet比traditional feedforward networks具有更优越的训练优势。这可通过改善网络中的梯度流量来解释。
ResNet的示意图如下:
为了方便理解,考虑 n n n-th和 m m m-th个残差单元,其中 m > n m>n m>n(即第 m m m个残差单元更接近输出层),通过多次残差递归, m m m-th个残差单元可表示为:
x m = x n + ∑ i = n m − 1 F ( x i , W i + 1 ) x_m=x_n+\sum_{i=n}^{m-1}F(x_{i},W_{i+1}) xm=xn+i=n∑m−1F(xi,Wi+1)
进一步,如果 L L L是模型训练的loss,可使用多元偏导数链式法则,将 L L L相对于第 n n n-th个RU输出 x n x_n xn的导数为:
∂ L ∂ x n = ∂ L ∂ x m ∂ x m ∂ x n = ∂ L ∂ x m + ∂ L ∂ x m ∑ i = n m − 1 ∂ F ( x i , W i + 1 ) ∂ x n \frac{\partial L}{\partial x_n}=\frac{\partial L}{\partial x_m}\frac{\partial x_m}{\partial x_n}=\frac{\partial L}{\partial x_m}+\frac{\partial L}{\partial x_m}\sum_{i=n}^{m-1}\frac{\partial F(x_{i},W_{i+1})}{\partial x_n} ∂xn∂L=∂xm∂L∂xn∂xm=∂xm∂L+∂xm∂Li=n∑m−1∂xn∂F(xi,Wi+1)
即:
∂ L ∂ W n = ∂ L ∂ x n ∂ x n ∂ W n = ( ∂ L ∂ x m + ∂ L ∂ x m ∑ i = n m − 1 ∂ F ( x i , W i + 1 ) ∂ x n ) ∂ x n ∂ W n \frac{\partial L}{\partial W_n}=\frac{\partial L}{\partial x_n} \frac{\partial x_n}{\partial W_n}=(\frac{\partial L}{\partial x_m}+\frac{\partial L}{\partial x_m}\sum_{i=n}^{m-1}\frac{\partial F(x_{i},W_{i+1})}{\partial x_n})\frac{\partial x_n}{\partial W_n} ∂Wn∂L=∂xn∂L∂Wn∂xn=(∂xm∂L+∂xm∂Li=n∑m−1∂xn∂F(xi,Wi+1))∂Wn∂xn
可以看到权重更新梯度依赖于两个信息源: ∂ L ∂ x m , ∑ i = n m − 1 ∂ F ( x i , W i + 1 ) ∂ x n \frac{\partial L}{\partial x_m},\sum_{i=n}^{m-1}\frac{\partial F(x_{i},W_{i+1})}{\partial x_n} ∂xm∂L,∑i=nm−1∂xn∂F(xi,Wi+1),可以看到后者中包含的信息主要取决于深度 n n n,**但前者提供的信息允许与深度无关。**因此,梯度可以不受阻碍的从deeper unit流向shallower unit,这促使可以训练更深的ResNet。
Full-Resolution Residual Networks (FRRNs)
论文统一上述两种设计原则,提出了和ResNet相同的优越训练属性的网络,具有两条处理流的full-resolution residual networks(FRRNs)。一条数据流称之为残差流(residual stream),通过连续添加残差计算。另一条数据流称之为池化流(pooling stream),是在输入上应用一连串的卷积和池化操作直接得到结果。
先不考虑网络的具体设计,获取high-level需要多个池化操作:
-
池化操作减少feature的空间分辨率的同时增加了模型接受野,这也是模型应对小型平移具有鲁棒性的根本。多次使用池化操作就很难追踪low-level的feature了(例如边沿,边界等)。这就让识别和准确定位产生了矛盾。(关于池化的这个问题在Object Detction讲了很多了~)。
-
如果网络不采取任何池化操作,这在目标边界定位上效果较好,但是识别性能差。
论文的设计思想源于网络模型需要联合high-level和low-level的feature。通过同时使用两条处理流,我们可以同时计算两种feature,残差流允许low-level的信息在网络内传播,池化流得到high-level的feature.两条处理流即如下图所示:
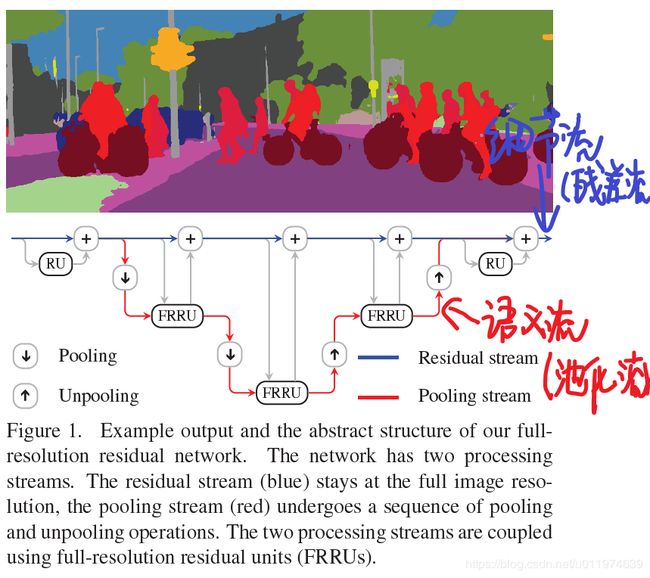
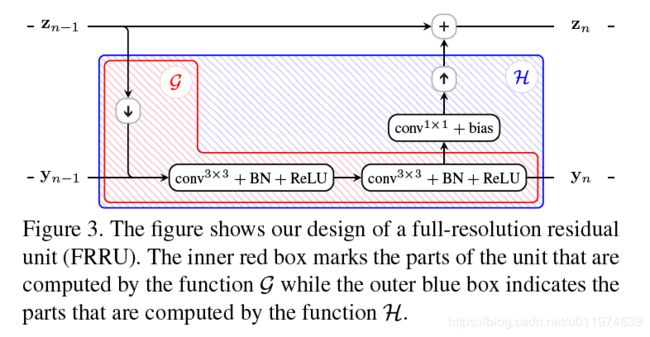
FRNN网络由一连串的full-resolution residual units(FRRUs)组成,每个FRRUs有两个输出和两个输入。如果 z n − 1 z_{n-1} zn−1为 n n n-th个FRRUs的残差输入, y n − 1 y_{n-1} yn−1为其池化输入,那么输出可计算为:
z n = z n − 1 + H ( y n − 1 , z n − 1 ; W n ) y n = G ( y n − 1 , z n − 1 ; W n ) z_n=z_{n-1}+H(y_{n-1},z_{n-1};W_n) \\ y_n=G(y_{n-1},z_{n-1};Wn) zn=zn−1+H(yn−1,zn−1;Wn)yn=G(yn−1,zn−1;Wn)
其中 W n W_n Wn是函数 G , H G,H G,H的参数。
FRRUs的示意图如下:
合理的配置函数 G , H G,H G,H才能组合两条流:
-
如果 G ≡ 0 G\equiv 0 G≡0,相当于丢弃了池化输入,那么
FRRUs就和原本的RU一个样子了。 -
如果 H ≡ 0 H\equiv 0 H≡0,没有残差结构了,那么
FRRUs就和traditional feedforward networks一个样子了。
同样论文也分析FRRNs和ResNet具有类似的训练特征,使用先前预设的递归参数,对于 m > n m>n m>n, z m z_m zm可表示为:
z m = z n + ∑ i = n m − 1 H ( y i , z i ; W i + 1 ) z_m=z_n+\sum_{i=n}^{m-1}H(y_i,z_i;W_{i+1}) zm=zn+i=n∑m−1H(yi,zi;Wi+1)
训练的loss记为 L L L,对于权重 W n W_n Wn的偏导数为:
∂ L ∂ W n = ∂ L ∂ z n ∂ z n ∂ W n + ∂ L ∂ y n ∂ y n ∂ W n = ( ∂ L ∂ z m + ∂ L ∂ z m ∑ i = n m − 1 ∂ H ( y i , z i ; W i + 1 ) ∂ z n ) ∂ z n ∂ W n + ∂ L ∂ y n ∂ y n ∂ W n \frac{\partial L}{\partial W_n}=\frac{\partial L}{\partial z_n}\frac{\partial z_n}{\partial W_n}+\frac{\partial L}{\partial y_n}\frac{\partial y_n}{\partial W_n} \\ =(\frac{\partial L}{\partial z_m}+\frac{\partial L}{\partial z_m}\sum_{i=n}^{m-1}\frac{\partial H(y_{i},z_i;W_{i+1})}{\partial z_n})\frac{\partial z_n}{\partial W_n}+\frac{\partial L}{\partial y_n}\frac{\partial y_n}{\partial W_n} ∂Wn∂L=∂zn∂L∂Wn∂zn+∂yn∂L∂Wn∂yn=(∂zm∂L+∂zm∂Li=n∑m−1∂zn∂H(yi,zi;Wi+1))∂Wn∂zn+∂yn∂L∂Wn∂yn
可以看到权重的更新依赖于三个信息源: ∂ L ∂ y n , ∂ y n ∂ W n , ∑ i = n m − 1 ∂ H ( y i , z i ; W i + 1 ) ∂ z n \frac{\partial L}{\partial y_n}, \frac{\partial y_n}{\partial W_n},\sum_{i=n}^{m-1}\frac{\partial H(y_{i},z_i;W_{i+1})}{\partial z_n} ∂yn∂L,∂Wn∂yn,∑i=nm−1∂zn∂H(yi,zi;Wi+1)。其中 ∂ L ∂ z m \frac{\partial L}{\partial z_m} ∂zm∂L是独立于深度的,这允许是用残差函数 H H H让所有参数实现了与深度无关的梯度流。
此外我们可以通过对 G G G计算的输出加权重,这样可通过 G G G的输出来计算 H H H.论文认为还有其他设计可能。
FRRUs设计如下:
- 首先使用池化层减少残差流的尺寸
- 再用concat操作将量两条流融合到一起
- 进过两个卷积单元(每个单元由 3 × 3 3×3 3×3卷积+BN层+ReLU组成)
- 这里一是直接出去下一层的池化流,另一个是输入到 H H H部分,作为计算残差的基础
蓝色部分 H H H是残差流操作:
- 池化函数 G G G输出经过 1 × 1 1×1 1×1卷积调整通道数目
- 再使用unpooling上采样(发现沿着空间维度简单的重复要比双线性插值要好)
可以看到池化函数 G G G的输出送到 H H H当输入, H H H包括了 G G G,这样的设计选择可为所有单元提供优越的梯度流动。
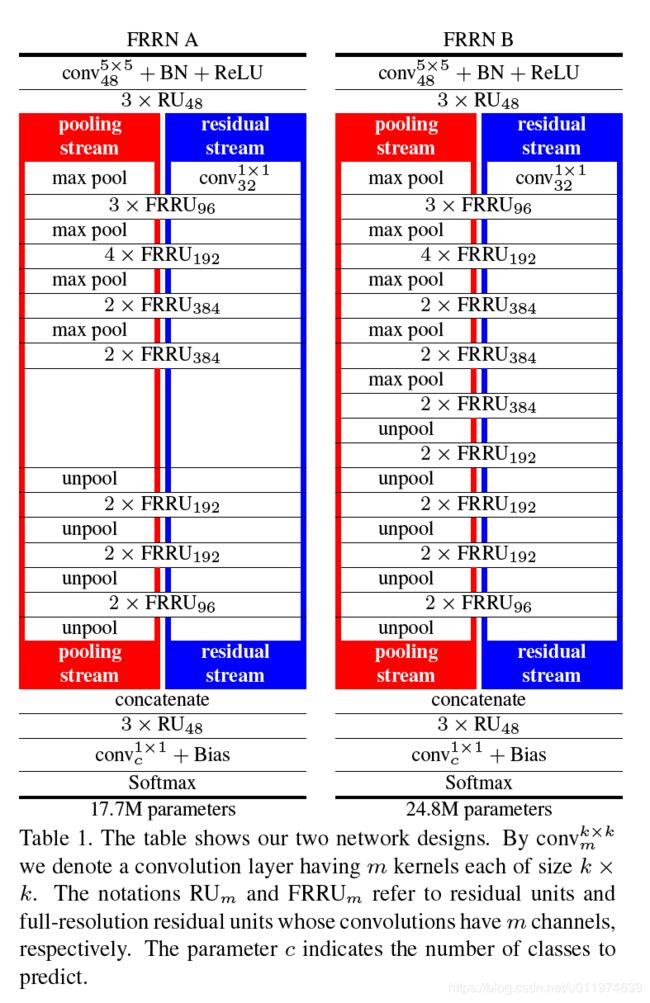
用来评估论文方案的两种网络架构:
架构使用的是encoder-decoder架构,在encoder阶段池化流使用最大池化,在decoder阶段使用双线性插值扩大feature。每次池化操作后将通道数增加一倍,不使用VGG网络的64通道,而是改成48通道合理控制训练参数。
Training Procedure
训练模型使用的是bootstrapped cross-entropy loss,记 c c c为分类类别。 y 1 , . . . , y N ∈ { 1 , . . . , c } y_1,...,y_N∈\{1,...,c\} y1,...,yN∈{1,...,c}作为像素 1 , . . , N 1,..,N 1,..,N的目标标签, p i , j p_{i,j} pi,j作为 i i i点预测种类 j j j的概率。对应 K K K个像素Loss定义为:
L = − 1 K ∑ i = 1 N 1 [ p i , y i < t K ] log p i , y i L=-\frac{1}{K} \sum_{i=1}^N1[p_{i,y_i}<t_K]\log p_{i,y_i} L=−K1i=1∑N1[pi,yi<tK]logpi,yi
其中如果 x x x为true,那么 1 [ x ] = 1 1[x]=1 1[x]=1。阈值 t K t_K tK对预测的对数概率做排序,并选择第 K + 1 K+1 K+1作为阈值.使用ADAM做优化。
可视化的情况:
因为FRRU处理了全分辨率的feature,这对内存要求非常高。为了做反正传播,需要将前向传播的值存储起来,但是这可能会超出GPU的显存。为了缓解这个问题,论文通过手动放置几个切割点将计算图分成若干个子块。独立的计算每个子块里面的导数。计算每个子块的前向传播,只存储用于方向传播的参数。这样允许我们在时间和空间上做折中。在测试期间,不要存储参数用于反向传播。
为了预防过拟合:训练时使用了两种数据增强
- 平移增强(translation augmentation),随机平移图片和对应的标注。为了填补平移后的留白,使用了反射填充和使用注释标签填充。
- γ \gamma γ增强(gamma augmentation):如下图所示
Experiment
论文测试了两种FRNNs网络:FRRN A在四分之一分辨率(256×512)的CityScapes上训练的;FRRN B在二分之一分辨率(512x1024)上训练。输出采用数双线性插值得到指定大小。虽然没有使用全分辨率,FRRN B已经表现了了具有竞争力的性能了。
Residual Network Baseline
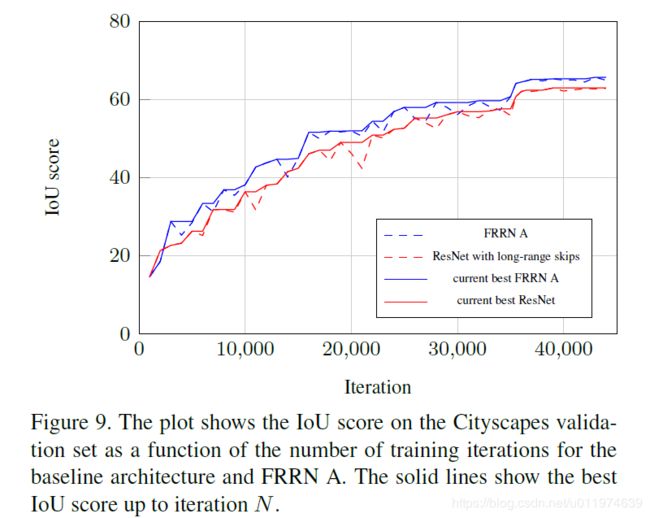
显示测试了FRRNs单元的有效性。测试了和FRRN A架构一致的网络,整体采用ResNet为基本单元且带skip-connection,正式的是FRRNs的baseline对比:
训练两个网络都使用1/4分辨率,迭代了45K,batchsize=3,前35K迭代学习率设置为 1 0 − 3 10^{-3} 10−3,后10K迭代学习率设置为 1 0 − 4 10^{-4} 10−4.正规的FRRN A相比于ResNet的性能有显著的提升。
FRRN效果要好点~
Quantitative Evaluation
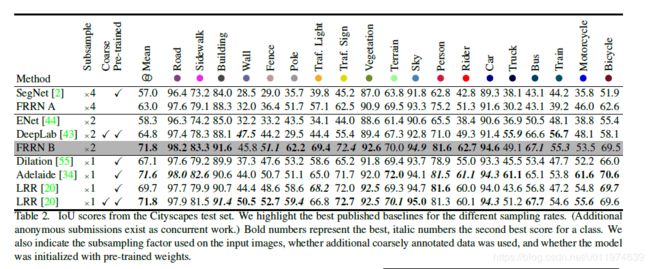
下表是在CityScapes测试榜上的对比结果:
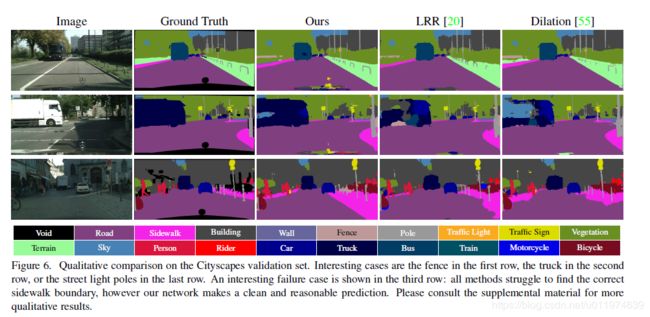
FRRN与其他模型预测结果可视化对比:
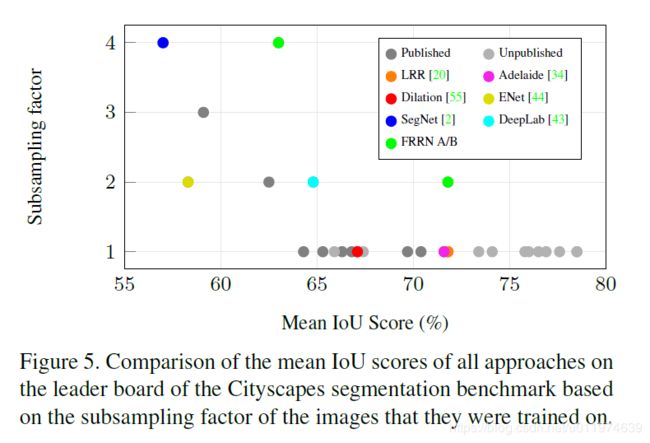
论文同时评估了上采样因子和性能之间的关系:
Boundary Adherence
对于语义分割任务,单独的去评估IoU指标不是太全面,因为池化操作会导致边界过于平滑,细节会丢失。常用的评估分割边界的方法是使用trimap evaluation.下表显示FRRN与其他先进模型对比:
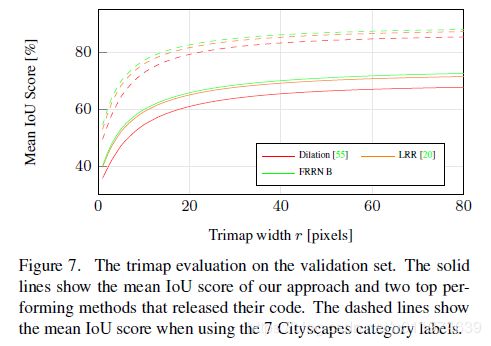
可以看到FRNN效果很棒。 同时论文了也测试CRF做后端处理,但是在性能上只有微弱的提升,鉴于CRF需要的大量计算,决定不做后端处理。
Conclusion
论文提出了一个面向城市街道场景语义分割任务的网络架构,模型不需要在其他模型上做预训练,在CityScapes上达到了state-of-the-art水准。且新的模型在边界分割上显示了强大的性能。