【论文阅读】改进的基于均值滤波的单幅图像去雾算法研究

改进的基于均值滤波的单幅图像去雾算法研究

吴延海，张婧，陈康
西安科技大学 学报, 2016

本文是在《基于单幅图像的快速去雾》基础上进行改进。主要改进有以下几点：

• 对《基于单幅图像的快速去雾》求出的L进行直方图修正。（也就是T的修正）
• 采用四叉树分裂算法求A，避免图中局部高亮雾图对A的影响。
• 对恢复的图像进行后处理。

1.投射图T

与《基于单幅图像的快速去雾》一样，求出：
$$V(x)=\min \left(\min \left(e{m}_{\mathrm{a}\mathrm{v}},0.9\right)M_{\mathrm{a}\mathrm{v}\mathrm{e}}(x),M(x)\right)$$
此处$V(x)=A(1-t(x))$。

此后对V进行修正。这里修正的原因是：

由于天空或明亮区域不满足暗原色先验规律，故造成大面积的色彩失真，均值滤波对天空区域或明亮区域的大气散射函数去雾力度过大，导致本来相差几个像素值被放大到几倍或几十倍，特别是当R，G，B三通道方向不一致时，所有的落差得到叠加，这就形成了天空或明亮区域的色彩失真。

ps：这里故事讲的有问题，其实原文基于均值滤波，并没有任何地方关系到暗通道先验，所以修正的理由有问题，问题提的有问题。

于是，作者经过大量实验（没有详细描述、证明）发现天空区域或者明亮区域的归一化直方图有以下特点：

• 天空区域的亮度值高于非天空区域，并且几乎不会交接；（天空区域亮度高，且近似空间连续）
• 天空区域在直方图右端分布较集中，表现为一个显著的尖峰。（天空区域在直方图的右端，即灰度值明显高区其他区域）

故本文提出一个天空区域的保护因子Thr（其实就是一个阈值），避免天空失真。（其实去雾中天空色彩失真的大部分原因是A值评估的不准确）。本文修正方法如下：

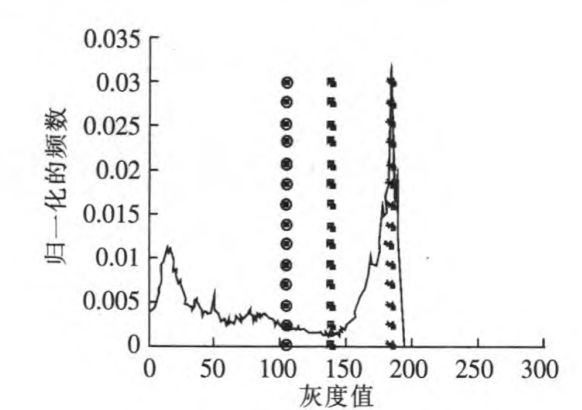
• 对V(x)做归一化直方图R(x)，取R(x)最大值点对应的灰度值为a。（如上图a=190，目测结果）。
• 利用大津法对R(x)进行阈值分割，即为b（上图b=100）。
• 在a、b之间找到直方图的最小极值点c（上图为c=140）。故Thrr=c=140.
• 实验中得出一个先验模式：$R(Thr)<0.0015$，则认为存在天空区域，此时$Thr=A-Thrr$，即直方图中尖峰宽度（[140，190]）；否则不存在天空区域，设定Thr=0.1。（感觉这里比较没有说服力，天空判断过于粗糙，难以应对复杂场景）。

至此，重新修正V得：
$$\begin{array}{c}V(x)=\min \left(\frac{abs(I-A)}{Thr},1\right)\cdot \omega \cdot \min (\min \left(e{m}_{\mathrm{a}\mathrm{v}},0.9\right)M_{\mathrm{a}\mathrm{v}\mathrm{e}}(x),M(x))\end{array}$$
其中$\omega =0.95$，表示去雾程度，与DCP论文一样。I为雾图。

2.大气光A

通常选择雾天退化图像中雾浓度最大的像素点的值作为大气光A的强度。但是实际场景往往是比较复杂，特别是存在明亮区域或白色物体时，大气光的估计会出现较大的偏差。而DCP论文采用按通道图最大的前0.1%像素点的最亮点作为A。但这种方法慢，而且途中存在白色物体时不准确。

本文采用四叉树分裂算法求A（该方法出自下文）。

Kim J H，Jang W D，Sim J Y，et a1．Optimized contrastenhancement for real-time image and video dehazing [J]．Journal of Visual Communication&Image Representation，2013，24(3)：410—425．

方法步骤：

• 首先求出图像的通道最小值
• 然后将通道最小值图像划分成4个区域，分别计算各区域平均亮度，取区域中均值最大的区域重复划分，直到该区域的大小小于给定阈值，一般设阈值为20×20。
• 最后根据所标记图像的位置计算原雾图中R，G，B通道中此块的均值作为A值。

附四叉树分裂算法matlab代码：

I = imread('img\example-02-haze.png');
% 1.注意图像size必须是2的n次方
I = imresize(I,[512 512]);
% 2.输入图像必须是单通道图像
I = rgb2gray(I);
S = qtdecomp(I,0.9);

% 在途中绘制四分结果
for dim = [512 256 128 64 32 16 8 4 2 1];   
  numblocks = length(find(S==dim));   
  if (numblocks > 0)   
    [values, r, c] = qtgetblk(I, S, dim);%读取S中所有尺寸为dim x dim的block，r和c是所有块的左上角点位置
    values(1:end,1,:)=0;%直接修改所有block的左、上边界为黑色。注意values是三维矩阵！！
    values(1,1:end,:)=0;
    I= qtsetblk(I,S,dim,values);%直接用修改后的block去替换S中的现有block
  end
end

I(end,1:end) = 0;
I(1:end,end) = 0;

figure, imshow(I,[])

3.图像色调调整（去雾结果后处理）

原因是恢复后的图相色调偏暗，所以需进行色调调整。不是重点，不再详细介绍，通常采用伽马校正也可。

4.本文的另一个有意义的地方是客观评价更为科学，采用可见边梯度法对去雾算法做客观评价。该盲评价方法出自下文

Hautiere N , Tarel J P , Aubert D , et al. Blind contrast enhancement assessment by gradient ratioing at visible edges.(Report)[J]. Image Analysis & Stereology, 2011, 27(2):87-95.

吴延海, 张烨, 马孟新. 基于NSCT变换和压缩感知的图像融合[J]. 西安科技大学学报, 2015(04):480-485.

该方法用复原后的新增可见边之比、可见边的规范化梯度均值和时间来评价图像的复原效果。
$$\begin{array}{rl}e& =\frac{n_{\mathrm{r}}-n_0}{n_0}\\ r& =\frac{{\overline{g}}_{\mathrm{r}}}{{\overline{g}}_0}\end{array}$$
$n_0$和$n_r$分别代表原图像和去雾图像中的可见边的数目，则e表示新增可见边的比例。${\overline{g}}_0$和${\overline{g}}_{\mathrm{r}}$分别表示原有图像和去雾图的平均梯度，通常e和r越大表示复原图像的质量越高。