机器学习：决策树（Decision Tree）

---

机器学习 深度学习 NLP 搜索推荐 等 索引目录

---

本博客参考邹博机器学习课件以及李航的《统计学习方法》，仅用于督促自己学习使用，如有错误，欢迎大家提出更正

---

决策树（decision tree）是一种基本的分类与回归方法。在分类问题中，它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。在学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型；在预测时，对新的数据，利用决策树模型进行分类。

1、决策树
1）决策树是一种树形结构，其中每个内部节点表示在一个属性上的测试，每个分支代表一个测试输出，每个节点代表一种类别。
2）决策树学习是以实例为基础的归纳学习，在本质上是从训练数据集中归纳出一组分类规则，其学习的策略是以损失函数（损失函数通常是正则化的极大似然函数）为目标函数的极小化。
3）决策树学习采用的是自顶向下的递归方法，其基本思想是以信息熵为度量构造一棵熵值下降最快的树，到叶子节点处的熵值为零，此时每个叶子节点中的实例都属于一类。

2、特征选择
特征选择在于选取对训练数据具有分类能力的特征，以提高决策树学习的效率。通常特征选择的准则是信息增益或信息增益比，在CART树里使用的是$Gini$指数。

2.1 信息增益（information gain）
首先来了解下熵和条件熵的定义。
**熵（entropy）**是表示随机变量不确定性的度量。设$X$是一个取有限个值的离散随机变量，其概率分布为
$$P(X=x_i)=P_i,i=1,2,...,n$$

则随机变量X的熵定义为
$$H(p)=-\sum _{i=1}^n{p}_{i}log(p_i)$$

在上式中的对数通常以2为底或以$e$为底（自然对数），这时熵的单位是比特（bit）或纳特（nat）.

条件熵（conditional entropy）
$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性。定义为$X$给定条件下随机变量$Y$的条件概率分布的熵对$X$的数学期望
$$H(Y|X)=-\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$

当熵和条件熵中的概率由数据估计（特别是极大似然估计）得到时，所对应的熵和条件熵分别成为经验熵和经验条件熵

**信息增益（information gain）**表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
定义：特征$A$对训练数据集$D$的信息增$g(D,A)$，定义集合$D$的经验熵$H(D)$与特征A给定条件下$D$的经验条件熵$H(D|A)$之差，即：

$$g(D,A)=H(D)-H(D|A)$$

一般地，熵与条件熵之差成为互信息（mutual information），决策树学习中的信息增益等价于训练数据集中类与特征的互信息。

根据信息增益准则的特征选择方法是：对训练数据集（或子集）$D$，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。

2.2 信息增益比（information gain ratio）
信息增益的大小是相对于训练数据集而言的，并没有绝对意义。在训练数据集的经验熵大的时候，信息增益值会偏大。反之，信息增益值会偏小。使用信息增益比可以对这一问题进行校正。
定义：特征$A$对训练数据集$D$的信息增益比$g_R(D,A)$定义为信息增益$g(D,A)$与训练集$D$的经验熵$H(D)$之比：
$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$

2.3 Gini指数
定义：分类问题中，假设有$K$个类，样本点属于第$k$类的概率为$p_k$，则概率分布的基尼指数定义为
$$Gini=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$

对于给定的样本集合$D$，其基尼指数为
$$Gini=1-\sum _{k=1}^K(\frac{C_k}{D}{)}^2$$
这里$C_k$是$D$中属于第$k$类的样本子集，$K$是类的个数。
基尼指数$Gini(D)$表示集合$D$的不确定性。基尼指数越大，样本集合的不确定性也就越大，这一点与熵值类似。
关于基尼指数的讨论，邹博老师也给出了如下图所示的解释：

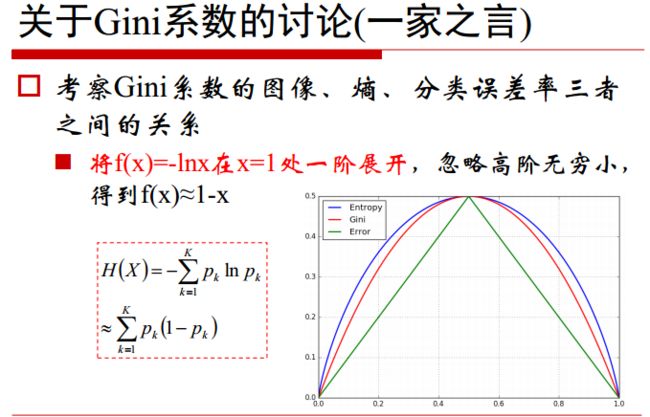
总结：一个属性的 信息增益(率)/$gini$ 指数越大，表明属性对样本的熵减少的能力更强，这个属性使得数据由不确定性变成确定性的能力越强。

3、决策树的生成
3.1 ID3算法
ID3算法的核心是在决策树各个结点上应用信息增益准则来选择特征，递归地构建决策树。ID3相当于用极大似然法进行概率模型的选择。
算法1 （ID3算法）
输入：训练数据集$D$，特征集$A$，阈值$\epsilon$；
输出：决策树$T$。
（1）若$D$中所有实例属于同一类$C_k$, 则$T$为单节点树，并将类$C_k$, 作为该节点的类标记，返回$T$；
（3）否则，计算$A$中各特征的对$D$的信息增益，选择信息增益最大的特征$A_g$；
（4）如果$A_g$的信息增益小于阈值$\epsilon$，则置$T$为单结点树，并将$D$中实例数最大的类为该节点的类标记，返回$T$；
（5）否则，对$A_g$的每一可能值$a_i$，依$A_g=a_i$将$D$分割为若干非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子节点，由结点及其子结点构成树$T$，返回$T$；
（6）对第$i$个子节点，以$D_i$为训练集，以$A-A_g$为特征集，递归地调用步（1）~步（5），得到子树$T_i$，返回$T_i$。

3.2 C4.5的生成算法
C4.5算法与ID3算法相似，C4.5是对ID3的改进，C4.5在生成的过程中，用信息增益比来选择特征，其他步骤与ID3一样。

3.3 CART算法
CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树，内部节点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征，将输入控件即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。
算法2（CART生成算法）
输入：训练数据集$D$，停止计算的条件；
输出：CART决策树。
根据训练数据集，从根节点开始，递归地对每个结点进行以下操作，构建二叉决策树：
（1）设结点的训练数据集为$D$，计算现有特征对该数据集的基尼指数，此时，对每一个特征$A$，对其可能取的每个值$a$，根据样本点对$A=a$的测试为“是”或“否”将$D$分割成$D_1$和$D_2$两部分，利用上述所给的$gini$求解公式计算$A=a$的基尼指数。
（2）在所有可能的特征$A$以及它们所有可能的切分点$a$中，选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点，从现结点生成两个子结点，将训练数据集依特征分配到两个子节点中去。
（3）对两个子节点递归地调用步骤(1)、(2)，直至满足停止条件。
（4）生成CART决策树。
算法停止的条件是节点中的样本个数小于预定的阈值，或样本集的基尼指数小于预定阈值，或者没有更多特征。

4、决策树的剪枝
决策树生成算法递归地产生决策树，直到不能继续为止，这样产生的树容易过拟合。过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树。解决这个问题的办法就是简化决策树，即剪枝。

三种决策树的剪枝过程算法相同，区别的仅是对于当前树的评价标准不同。（信息增益，信息增益率，基尼指数）

通常情况下剪枝有两种：

先剪枝——在构造过程中，当某个节点满足剪枝条件，则直接停止此分支的构造。
后剪枝——先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

剪枝的总体思路：

• 由完全树$T_0$开始，剪枝部分结点得到$T_1$，再次剪枝部分结点得到$T_2$，…，直到仅剩树根的树$T_k$;
• 在验证数据集上对这$K$个树分别评价，选择损失函数最小的树$T_{\alpha }$

决策树的剪枝往往通过极小化决策树整体的损失函数（loss function）或代价函数（cost function）来实现。设树$T$的叶结点个数为$|T|$，$t$是树$T$的叶结点，该叶节点有$N_t$个样本点，其中k类的样本点有$N_{tk}$个，$k=1,2,...,K$，$H_t(T)$为叶节点$t$上的经验熵，$\alpha \ge 0$为参数，则决策树学习的损失函数可以定义为：
$$C_{\alpha }(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$
其中经验熵为
$$H_t(T)=-\sum _k\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}$$

在上述损失函数的式中，第一项表示模型对训练数据的预测误差，$|T|$表示模型复杂度，参数$\alpha \ge 0$控制两者之间的影响，较大的$\alpha$促使选择较简单的模型（树），较小的$\alpha$促使选择较复杂的模型（树）。$\alpha =0$意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度。
剪枝，就是当$\alpha$确定时，选择损失函数最小的模型，即损失函数最小的子树。利用损失函数的极小化等价于正则化的极大似然估计进行模型选择。
剪枝系数$\alpha$的确定，如下所示：

剪枝算法：