c++实现二叉堆及堆排序

一、什么是二叉堆

       二叉堆在数据结构上是完全二叉树。完全二叉树即：除了最后两层的节点外，所有节点具有两个子节点的二叉树。最底层的数据按照从左到右依次排列。

同时，节点满足：父节点存储的值总是大于或者总是小与子节点的存储的值。

最大堆：父节点的键值总是大于或等于任何一个子节点的键值。

最小堆：父节点的键值总是小于或等于任何一个子节点的键值。

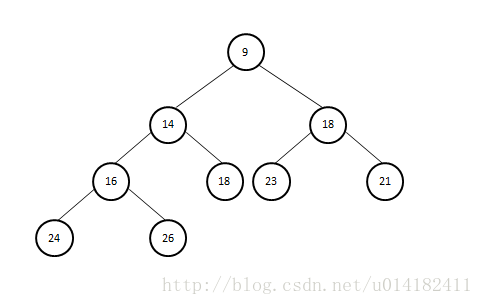
如下图所示，图a是一个二叉堆，而图b不是。

                                            图a

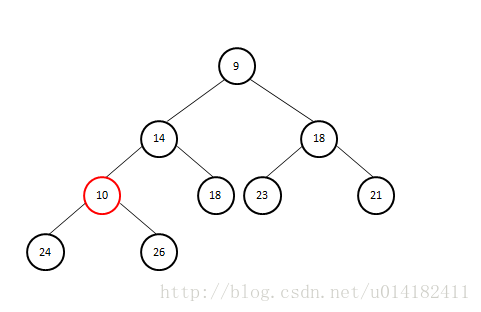
                                                 图b

二、二叉堆的特点

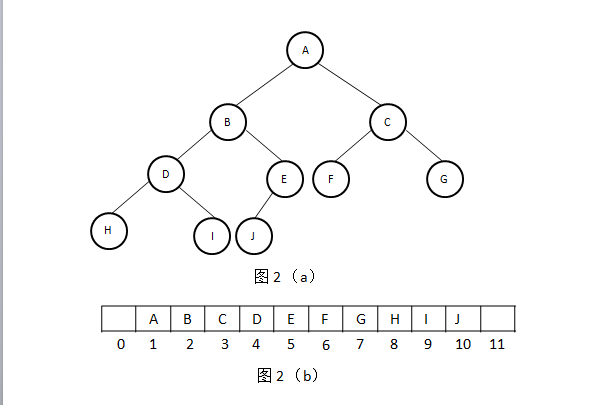
   因为完全二叉树的特殊性，可以使用数组来存储而不用链式存储。如下图2所示，图2（a）中的数组对应图（b）中的二叉堆。

从图中可以看出：数组中i元素对应的左子树在数组的2i的位置上，右子树在2i+1的位置上，其父亲在floor(i/2)的位置上。

利用该特性很容易在用数组存储的二叉堆中找出一个节点的左右子树和父亲节点。

三、c++实现二叉堆的基本操作

       二叉堆的一切操作建立与堆中父节点存储的值总是大于或者总是小与子节点的存储的值。以下我们均讨论的是父亲节点存储的值小与子节点存储的值的情况。

1、二叉堆的数据结构定义 

BinaryHeap.h文件：

#include 
using std::vector;
template < typename T>
class BinaryHeap {
public:
    BinaryHeap (int capacity = 100) ;
    BinaryHeap (vector &item) ;
    ~BinaryHeap(){}
    bool isEmpty ();
    void insert (const T & x);
    void deleteMin ();
    void deleteMin (T & minItem);
    void makeEmpty ();
    void showHeap();
private:
    int currentSize;
    vector array;
    void percolateDown (int hole);
    void buildHeap ();
};

2、二叉堆的插入

       向二叉堆中插入一个数需要保持二叉堆的特性。首先，我们将待插入的数x插入到二叉树的空位中，即数组的最后一个位置。如果x的插入没有破坏掉二叉堆的

特性，则插入完成。显然，这种情况比较特殊，大多数情况下是x的插入破坏了二叉堆的特性。这种情况下，x 的值小于了父亲节点的值，我们只需要交换x与父亲

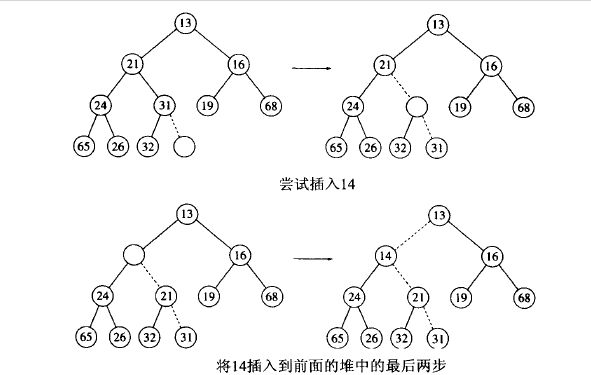
节点的值，然后再次进行上诉比较，直到x的不小于父亲节点的值或者x被放到了根节点的位置。这个过程称为上滤。上滤过程最多需要进行logN次交换，每次交换

是常数时间。所以，插入的时间复杂度是O(logN)。以下例子说明该过程（途中白圈位置是14不断推进的位置）

代码实现如下：

template<typename T>
void BinaryHeap::insert(const T &x) {
    if (currentSize == array.size() - 1) {
        array.resize(array.size() * 2);
    }
    int hole = ++currentSize;
    /*将需要插入的值与当前树中的最后一个元素的父元素做比较，若父元素大于x,则将父元素移到当前子元素的位置
     * 直到父元素小与等于x,则x插入当前子元素的位置。
    */
    for (; hole > 1 && x < array[hole / 2]; hole /= 2) {
        array[hole] = array[hole / 2];
    }
    array[hole] = x;
}

在该实现过程中，一开始我们没有插入x,而是不断将一个空的数推向x应该在的位置。最后才在这个位置插入x。这样做的好处是避免了每次向上推x的时候，需要x

与父亲节点的值进行交换，这样节省了3步交换的步骤。

3、二叉堆的删除

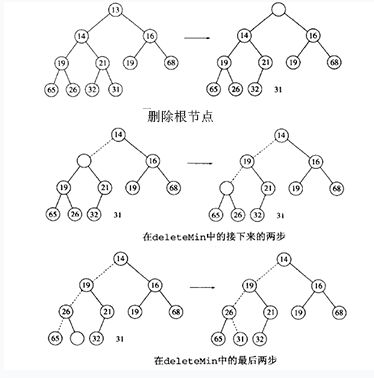
         二叉堆的删除这里值得是删除所有元素中最小的那一个。显然，最小的那一个数是根节点处的树。删除很容易，只需要常数事件。关键是删除根节点之后，如

何保证剩余数的二叉堆特性。在这里，我们采取将二叉堆中最后一个数x放到根节点处，然后采取与插入相似的操作：将x不断与其两个子节点中最小的那一个比

较。若最小的子节点小于x，则交换两个数，直到x的两个子节点均不小于x。这一过程称为下滤。同样，最多需要进行logN次交换，每次交换是常数时间。所以，

删除的时间复杂度是O(logN)。以下一个列子说明该过程。    

实现代码：

template<typename T>
void BinaryHeap::deleteMin() {
    if (isEmpty()) {
        std::cout << "The heap is empty!" << std::endl;
    }
    //将array中最后一个数赋值给第一个元素，array元素个数减一；然后开始下滤
    array[1] = array[currentSize--];
    percolateDown(1);
}

template<typename T>
void BinaryHeap::deleteMin(T &minItem) {
    if (isEmpty()) {
        std::cout << "The heap is empty!" << std::endl;
    }
    minItem = array[1];
    //将array中最后一个数赋值给第一个元素，array元素个数减一；然后开始下滤
    array[1] = array[currentSize--];
    percolateDown(1);
}

template<typename T>
void BinaryHeap::percolateDown(int hole) {
    T x = array[hole];
    int child;
    /*找出当前父元素的子元素中最小的一个child，然后和父元素比较，如果child小与父元素，
     则将child的值赋给父元素，直到父元素的值小与等于子元素的值，此时将x的值赋给这个父元素终止循环 */

    for (; hole * 2 <= currentSize; hole = child) {
        child = 2 * hole;
        if (child != currentSize && array[child + 1] < array[child])
            child++;
        if (array[child] < x)
            array[hole] = array[child];
        else
            break;
    }
    array[hole] = x;
}

我们提供两个版本的deleteMin()，其中带参数的deleteMin(T & minItem)可以通过传址的方式返回删除的最小点的值。

percolateDown()完成下滤操作。同插入操作一样，我们在最后才在应该插入x的位置插入x，从未避免中间多次交换带来的操作。

4、二叉堆的创建

用vector初始化array后，再从二叉堆中的倒数第二层中的最后一个数到根节点，进行下滤操作。最坏的操作次数是二叉堆中所有节点的层高之和（叶子节点的层高

为0）。可以通过证明得到二叉堆的创建的时间复杂度是O(N)。以下一个例子说明创建过程：

代码如下：

template<typename T>
BinaryHeap::BinaryHeap(int capacity)
        : array(capacity+10), currentSize(capacity) {
}

template<typename T>
BinaryHeap::BinaryHeap(vector &item)
        : array(item.size() + 10), currentSize(item.size())
{
    for (int i = 0; i != item.size(); i++)
        array[i+1] = item[i];
    buildHeap();
}

template<typename T>
void BinaryHeap::buildHeap() {
    for (int i = currentSize / 2; i > 0; i--)
        percolateDown(i);
}

四、基于二叉堆的堆排序

      从以上的二叉堆操作中，我们可以看出，每次删除的数是二叉堆中最小的数，利用这个性质，我们可以将需要排序的数用于创建一个二叉堆，时间复杂度是

O(N)，再N次删除二叉堆中的数，这样得到的删除的序列就是这组数按照从小到大的排序。每次的删除操作的事件复杂度是O(logN)，总共N次，时间复杂度是

O(NlogN)。总的时间复杂度就是O(N+NlogN)=O(NlogN)

测试如下：

main.cpp:

#include 
using namespace std;
#include "BinaryHeap.h"
#include "BinaryHeap.cpp"


int main() {
    vector<int> vector1 = {3,5,6,7,2,10,1,4};
    BinaryHeap<int> BHeap(vector1);
    cout << "The binary heap is:" << endl;
    BHeap.showHeap();
    int min;
    cout << "The result of ascending order:" << endl;
    for (int i = 0; i < vector1.size(); i++) {
        BHeap.deleteMin(min);
        cout << min << " ";
    }
    cout << endl;
    return 0;
}

测试结果：

The binary heap is:
1 2 3 4 5 10 6 7
The result of ascending order:
1 2 3 4 5 6 7 10

五、参考

   参考书：数据结构与算法分析第三版

   整个二叉堆的工程文件在本人github上可以查阅：

   https://github.com/yuanzoudetuzi/binaryHeap