基数估计算法(二)：Linear Counting算法

写作不易，转载请注明出处:
http://blog.csdn.net/wbin233/article/details/78752597 ，谢谢。

简介

Linear Counting是KYU-YOUNG WHANG，BRAD T. VANDER-ZANDEN和HOWARD M. TAYLOR大佬们1990年发表的论文《A linear-time probabilistic counting algorithm for database applications》中提出的基于概率的基数估计算法。

基本思想及实现

Linear Counting的实现方式非常简单。
首先定义一个hash函数：
function hash(x): -> [0,1,2,…,m-1]，假设该hash函数的hash结果服从均匀分布。

接着定义一个长度为m的bit数组，开始每一位上都初始化为0.

然后对可重复集合里的每个元素进行hash得到k，如果bitmap[k]为0则置1。

最后统计bitmap数组里为0的位数u。

设集合基数为n，则有：
n^=−mlnum ，且其为n的最大似然估计。

---

简单的伪代码如下：

---

举个例子说明下吧，如下：

集合中共有11个元素，hash函数映射到[0,7]中（m=8）且结果服从均匀分布。如图hash结果后共有2个bit为0，即u=2。代入上述公式可得估计结果为11.1(实际值为10)。
【该例子只为了说明算法的过程，实际中都是大数据中估计。】

公式证明

先说明下述中使用到的变量。

变量	含义
n	基数
q	总数
m	bit数组的长度（hash区间）
t	n/m
Un	hash后bit数组为0的位数
Vn	Un/m
p	E(Vn)

---

由于hash函数映射后的hash结果服从均匀分布，因此任意一数选中bitmap数组的某一个bit概率为 1m 。
设 Aj 为事件“经过n个不同元素哈希后，第j个桶值为0”，则：
P(Aj)=(1−1m)n ,
P(Aj∩Ak)=(1−2m)n,j≠k.

又每个bit是相互独立的，即 Aj 服从均匀分布。
则 Un 的数学期望为：
E(Un)=∑mj=1P(Aj)=m(1−1m)n=m(((1+1−m)−m)−nm)≅me−nm=me−t,当n,m→∞

【数学上证明： limx→∞(1+1x)x=e 】

所以： E(Un)=me−nm

即： n=−mlnE(Un)m

显然，bitmap里每个bit的值服从相同的0-1分布，因此 Un 服从二项分布。
由概率论与数理统计知识可知，当n很大时，可以用正态分布逼近二项分布，因此可以认为当n和m趋于无穷大时 Un 渐进服从正态分布。
由于我们观察到的空桶数 Un 是从正态分布中随机抽取的一个样本，因此它就是μ的最大似然估计（正态分布的期望的最大似然估计是样本均值）。

又由如下定理：

设f(x)是可逆函数且 x^ 是x的最大似然估计，则f( x^ )是f(x)的最大似然估计。
且 −mlnxm 是可逆函数，则 n^=−mlnUnm 是 n=−mlnE(Un)m 的最大似然估计。

Un和Vn的期望和方差

先给出结论，在 m,n→∞ 的前提下有：
E(Un)=me−nm=me−t.

Var(Un)=me−t(1−(1+t)e−t).

又有 Vn=Unm，

E(Vn)=e−t.

Var(Vn)=1me−t(1−(1+t)e−t).

---

详细推导过程如下：

通过上文，我们已经可以获得 Un 的数学期望为：
E(Un)=me−nm=me−t，asm,n→∞

则 U2n 的数学期望为：
E(U2n)
=E((∑mj=1P(Aj))2)
=E(P(A1)∗P(A1)+P(A1)∗P(A2)+...+P(A1)∗P(Am)+P(A2)∗P(A1)+...+P(Am)∗P(Am))
=E(∑mj=1A2j)+2E(∑mj=1∑j−1i=1P(Ai)∗P(Aj))
=m(1−1m)n+2(m(m−1)2)(1−2m)n，asm,n→∞

因此，可以计算 Un 的方差(variance)：
Var(Un)
=E(U2n)−E(Un)2
=m((1−1m)n+(m−1)(1−2m)n−m(1−1m)2n)
=m((1−1m)n−(1−2m)n+m((1−2m)n−(1−1m)2n))
=m(((1+1−m)−m)−nm−((1+1−m2)−m2)−2nm+m((1−2m)n−(1−1m)2n))
≅m(e−t−e−2t−te−2t)，asm,n→∞
=me−t(1−(1+t)e−t)，asm,n→∞

在上述计算过程中，我们近似了
m((1−2m)n−(1−1m)2n)≅−te−2t .

具体推导过程如下：


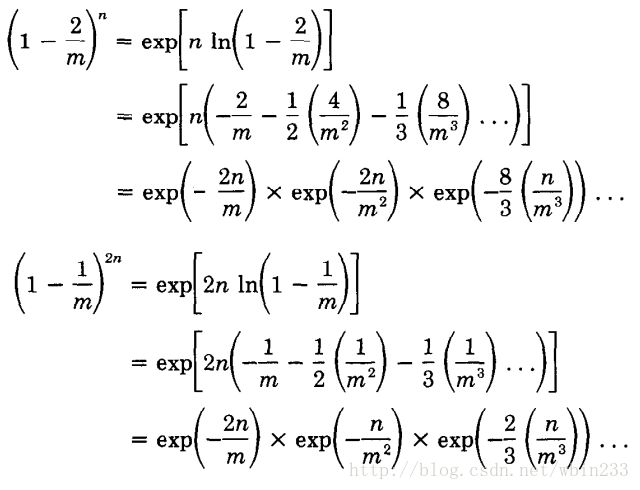
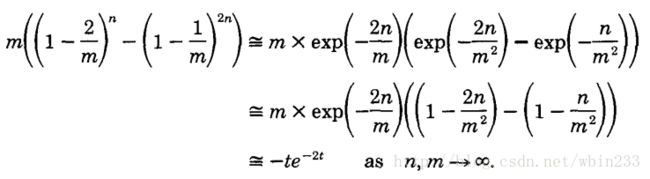
其中用到了泰勒展开：
ln(1+x)=x−x22+x33−x44+...,−1<x≤x

又 Vn=Unm ，因此可以计算 Vn 的期望和方差：

E(Vn)=1mE(Un)=e−t，asm,n→∞

Var(Vn)=1m2Var(Un)=1me−t(1−(1+t)e−t)，asm,n→∞

偏差- Bias(n^n) 的计算

同样的，先给出结论：
Bias(n^n)=E(n^n)−1=et−t−12n .

可以得到Bias,t和n之间的关系，如下图：

---

详细推导如下：
Vn=Unm，且n^=−mlnUnm 。
因此可以写成： n^=−mlnVn .

令 p=E(Vn)=e−t，f(Vn)=−ln(Vn) .

由著名的泰勒展开公式有：

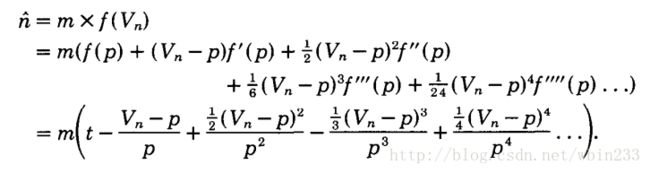
保留泰勒展开里的第一项和第三项（原因翻阅论文，有点儿复杂），得：
E(n^)=mt+m2p2E(Vn−p)2.

之前已经计算过， E(Vn−p)2=Var(Vn)=1me−t(1−(1+t)e−t) .

代入得： E(n^)=n+et−t−12 .

因此， Bias(n^n)=E(n^n)−1=et−t−12n .

标准误差- StdError(n^n)的计算

StdError(n^n)=m√(et−t−1)12n

可以得到StdError,t和n之间的关系，如下图：

---

这一次，在 n^=m∗f(Vn) 的泰勒展开式中，保留前两项，得：
n^=m(t−Vn−pp).
可得：

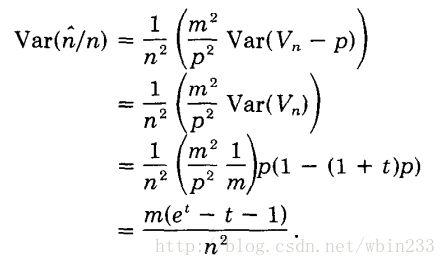
因此， n^n 的标准误差(standard error)为：
StdError(n^n)=m√(et−t−1)12n

bit数组的长度m的选取

先给出结论，m应该满足：
m>β(et−t−1)，其中β=max(a2,1(ϵt)2)

ϵ 表示用户容许的标准误差(standard error)；

a表示 Un 与0的偏差倍数。
【下文给出结论，当 a>5√即E(Un)>5√StdDev(Un) 时， P(Un=0)<0.007. 】

---

详细推导如下：

1.证明 m>et−t−1(ϵt)2.

假设用户容许的标准误差(standard error)为 ϵ ，则根据上面标准差公式可以得到：
StdError(n^n)=m√(et−t−1)12n<ϵ
转化得：

m>et−t−1(ϵt)2.
因此给定容许的误差 ϵ 以及相应的量级t，可求出满足该情况的相应m的大小。

2.证明 m>a2(et−t−1)

显然，如果m远小于n，则显然出现满桶的概率特别大，因此计算不出结果【因为 Un=0 ，代入公式结果为无穷大】。

因此m的选择除了要满足上面误差控制的需求外，还要保证满桶的概率非常小。

我们可以让空bit的位数与0有一个a倍的偏差。即：
E(Un)−a∗StdDev(Un)>0.

其中， E(Un)=me−t，StdDev(Un)=me−t(1−(1+t)et)−−−−−−−−−−−−−−−√

因此可得： me−t>ame−t(1−(1+t)et)−−−−−−−−−−−−−−−√

化简之： m>a2(et−t−1)

综上，m应该满足：

m>β(et−t−1)，其中β=max(a2,1(ϵt)2)

满桶控制

由概率论与数理统计中可知，当n非常大，p非常小时，可以用泊松分布(Poisson distribution.)近似逼近二项分布。

如果 me−nm→λasn,m→∞.
则认为 Un 服从泊松分布。

即： limn,m→∞Pr(Un=k)=λkk!e−λ.

E(Un)=me−nm=λ.

因此满桶的概率为：
Pr(Un=0)=e−λ.

当 a>5√ 时，有 E(Un)>5√StdDev(Un).

又因为泊松分布中，数学期望E(x)和方差Var(x)均等于 λ ，
所以 E(Un)=Var(Un)=λ，StdDev(Un)=λ√ 。

代入得： λ>5λ−−√ ，即 λ>5

所以： Pr(Un=0)=e−λ<e−5=0.007(0.7%).
意味着当 a>5√ 时，满桶的概率小于0.7%。

---

根据 m>β(et−t−1)，其中β=max(a2,1(ϵt)2)

利用二分法(bisection method)，给出当a= 5√ (满桶概率小于0.7%)时，不同基数数量级以及标准误差(0.01和0.1)时，m的选择表：

其中，
当 ϵ=0.01 时， 1(ϵt)2 决定 β ；

当 ϵ=0.1 并且 n≤1000 时， 1(ϵt)2 决定 β ；

当 ϵ=0.1 并且 n>1000 时， a2 决定 β ；

从表中也可以看出精度要求越高( ϵ=0.01 )，则bitmap的长度越大。
并且随着m和n的增大，m大约为n的十分之一。

所以Linear Counting的空间复杂度仍为 O(N) 。

合并

Linear Counting非常方便于合并，直接通过按位或的方式即可。

参考资料

• WHANG, K.-Y., VANDER-ZANDEN, B., AND TAYLOR, H. A linear-time probabilistic counting algorithm for database applications. ACM Transactions on Database Systems 15, 2 (1990), 208–229.
• http://blog.codinglabs.org/articles/algorithms-for-cardinality-estimation-part-ii.html