hhh还是滚去学了插头DP。。。
这玩意理解起来其实并不是听说的那么困难。(那是因为你只写了板子QAQ
我太菜了所以可能写了一堆锅,所以哪位爸爸发现了错误指出来就好。谢谢orz!
基本概念
Q:插头DP是啥?
A:基于连通性状态压缩的动态规划
Q:它可以干嘛?
A:不是说了嘛...基于连通性状态压缩的动态规划嘛分为两类,骨牌覆盖&线段覆盖
Q:啥时候用?
A:网格,数据范围极小,可以状态压缩。大部分为计算方案。
Q:插头是啥?
A:格子与格子中间的转移,可以理解为拼图的缺口和凸起。
Q:轮廓线是啥?
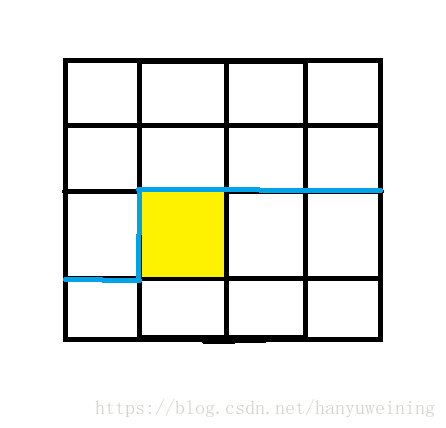
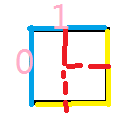
A:轮廓线就是我们状态压缩的部分。就是当前处理完的和未处理的分界线。
蓝色的就是轮廓线,黄色的使我们接下来要处理的格子。
步入正题
我们直接看陈丹琦论文里的入门题好了。BZOJ1814:Formula 1(URAL1519)
题目大意:给出一个m*n的矩阵里面有一些格子为障碍物,求经过所有非障碍格子的哈密顿回路个数。
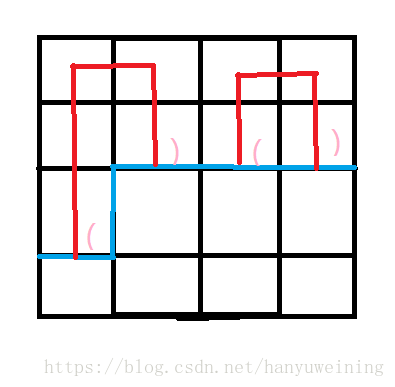
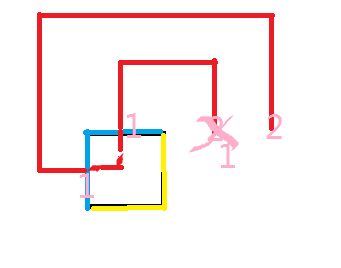
我们先介绍一下这个最小表示法。首先哈密尔顿回路不会出现两条路径交叉(可以自己YY一下),所以一条路径就可以看成左右括号,然后多条路径就是一个括号匹配。如下图
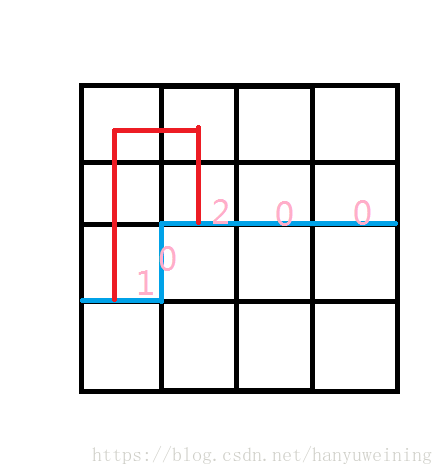
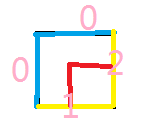
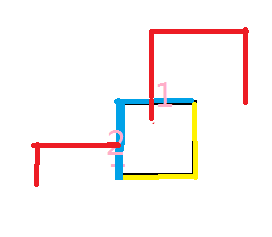
所以对于一段路径,它的左边接入点称之为1,右边接入点称之为2。以及没有接入点的地方表示为0。这样我们就可以状压表示路径的连通性啦。因为我们是从左到右,从上到下转移,所以对于一个格子它会有一个上插头,一个左插头,分别为上方接入的地方是啥以及左边的接入点是啥。
这是一个三进制状态,需要手写位运算,并不是很方便,所以我们就可以把它看成4进制,在开始的时候预处理一下每个数*2的结果,然后4^x就可以表示为2^2x啦。然后我们又发现4^x存不下啊怎么办。这时候我们可以使用哈希表,然后开两个数组f,g分别维护状态&答案。
状态解决了接下来我们就可以转移了。
前面我们提到过其实就是一个括号匹配问题。所以接下来可以同时利用括号匹配的思路方便理解。
我们先讨论这个格子没有障碍物。(轮廓线均为蓝->黄)
00 -> 12 即开始一段新路径
01->01 or 10 虚线的两种连法
同理得到
10 ->01 or 10
02 ->02 or 20
20 ->02 or 20
然后我们就有复杂一点的了
11->00 同时需要把右边的第一个2改为1 因为两个路径合并为一条路径了。
22->00同理 将左边的第一个1改为2
21->00 我们合并了两条路径
!!!!12->00!!!!
这个不可以乱来,因为我们把整条回路封闭了!!!
所以只有最右下方的一个空格子可以封闭回路。
【不画图了,最后一个你自己YY好了QwQ】
然后我们还有一个障碍格子没有处理。首先它不能被接入也不能接出所以就是00->00【障碍格子只可以有这一种转移】
然后我们就可以写代码啦!写起来有爆搜的感觉hhh
#include
#include
#include
#include
#define md 312251
#define mxn 15
using namespace std;
int mp[mxn][mxn],hs[md+2],k,n,m,nn,mm;
unsigned long long f[2][600000];long long ans,g[2][600000];
char ch[mxn];
//f:state g:sum
int tot[2],mi[mxn];
void prework()
{
for(int i=1;i<=max(n,m);i++)
mi[i]=i<<1;
}
void put(unsigned long long cur,long long val)
{
int s=cur%md;
while(hs[s])
{
if(f[k][hs[s]]==cur)
{
g[k][hs[s]]+=val;
return;
}
s++;if(s==md) s=0;
}
hs[s]=++tot[k];f[k][hs[s]]=cur;g[k][hs[s]]=val;
}
void solve()
{
tot[0]=1;g[0][1]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
k^=1;tot[k]=0;
memset(hs,0,sizeof(hs));
memset(f[k],0,sizeof(f[k]));
memset(g[k],0,sizeof(g[k]));
for(int u=1;u<=tot[k^1];u++)
{
unsigned long long state=f[k^1][u];
long long val=g[k^1][u];
int p=(state>>mi[j-1])%4,q=(state>>mi[j])%4;
if(!mp[i][j])
{
if(!p&&!q) put(state,val);
}
else
{
if(!p)
{
if(!q)
{
if(mp[i+1][j]&&mp[i][j+1])
put(state+1*(1<>mi[v])%4;
if(s==1) cur++;
if(s==2) cur--;
if(!cur)
{
s=state-p*(1<=1;v--)
{
s=(state>>mi[v])%4;
if(s==2) cur++;
if(s==1) cur--;
if(!cur)
{
s=state-p*(1< 哦对了。当我们转移完一行的时候,状态需要*4,也就是整体左移一次。这个是因为我们在计算的时候整体右移了一发。所以需要移回去。我觉得我写的十分可读QwQ
好了就到这里吧。。。下个题。。。等我想放的时候再放好了hhh【原因是我今天早晨应该学LCT的,学到一半把LCT咕了QAQ