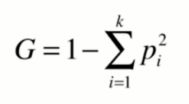机器学习----决策树学习记录、信息熵详解

什么是决策树？

决策树是广泛用于分类和回归的模型，本质上是一层层if/else问题中进行学习，并得出结论的。

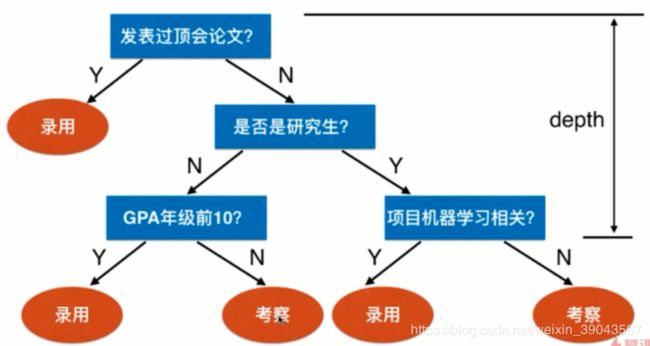
决策树的思路在生活中很常见，比如公司招聘一个机器学习工程师流程：

这一系列问题呢就可以表示一颗决策树，树的每一个叶子节点代表一个问题或者结果。即为了分类录用和考察，利用三个特征论文、研究生、GPA、项目来构建一个模型。

下面简单用鸢尾花数据实现以下：

import numpy as np
import matplotlib.pyplot as plot
from sklearn import datasets
iris = datasets.load_iris()
X=iris.data[:,2:]
y=iris.target

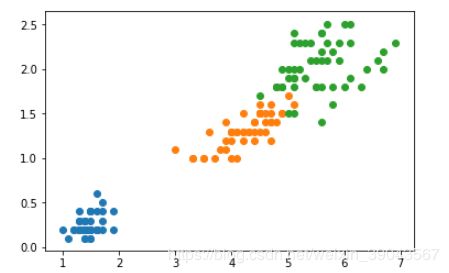
plot.scatter(X[y==0,0],X[y==0,1])#y==0时索引对应X的特征，即类别0使对应的X
plot.scatter(X[y==1,0],X[y==1,1])
plot.scatter(X[y==2,0],X[y==2,1])

from sklearn.tree import DecisionTreeClassifier
#构建函数，max_depth决策树深度，criterion使entropy（熵下面介绍）
dt = DecisionTreeClassifier(max_depth=2,criterion="entropy") 
dt.fit(X,y)

y_predict=dt.predict(X)#使用训练模型看看结果
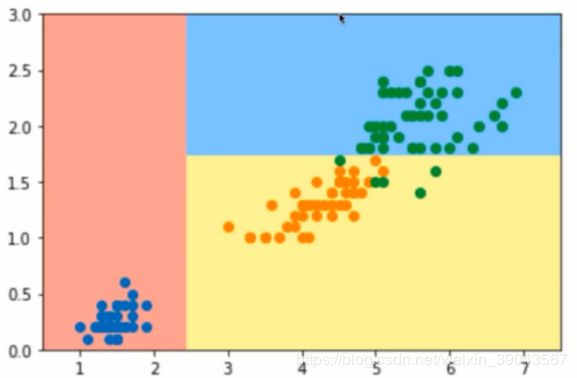
np.sum(y_predict==y)/len(y)#看看预测准确率

0.96

画出这个决策树生成的决策边界：

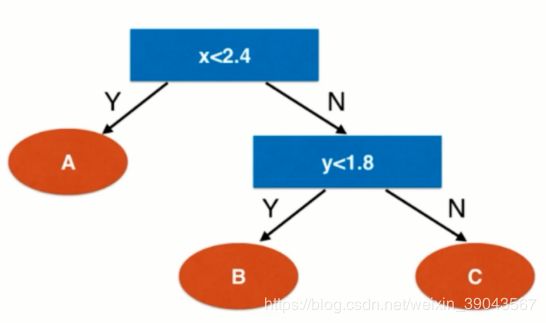
在面对属性是数值型特征时如何分类的，在每一个节点上选择某一个维度和相应的阈值（比如上面x<2.4，y<1.8），数据点到每一个节点都会进行一次分类。比如新数据点(2.5，2)  --> x<2.4?   -NO->  y<1.8?   -NO->  C类！

决策树时非参数学习算法，可解决分类、回归。回归问题预测的最终的值时最后叶子节点所有样本数据的平均值 。

可解释性好，每一步都能知道最终的分类时怎么来，依据可观察。

核心问题：每个节点在哪个维度上划分，某个维度上的哪个值进行划分？

信息熵

每个节点在哪个维度上划分，某个维度上的哪个值进行划分？计算信息熵是解决这个问题的一个方法。

熵在信息论中代表随机变量不确定度的度量，熵越大数据的不确定性越高，熵越小数据的不确定性越低。

信息熵表示的是不确定度。均匀分布时，不确定度最大，此时熵就最大。

其公式为：

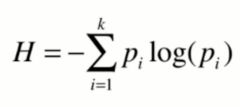其中，pi代表每个类别所占的比例，比如10个数据点，1类3/10，2类3/10，3类4/10，那么p1，p2，p3就是3/10，3/10，4/10。H=-p1log(p1)-p2log(p2)-p3log(p3) 。熵H肯定是大于0的，pi一定是小于1的数，所以前面要加上-号。

举个例子更好的理解什么是熵：

假如我们有3个类别的数据点，每个类别各占1/3，那么H=-1/3log(1/3)-1/3log(1/3)-1/3log(1/3) = 1.0986

假如每个类别占{1/10，2/10，7/10}， 那么同上算法H=0.8018

假如{1，0，0} 即都是第一类，没有其他类，此时H=-1log(1)=0

通过以上我们可以知道， 信息熵表示的是不确定度，越小不确定程度月低，即确定程度很高（毕竟某个类占的很多啊！），而三个类别均匀比例分布时，信息熵很大，说明不确定程度高，即我们很难确定哪一类。

以上我们大概就明白了什么时信息熵。

还不明白的话我们就在画个图图瞅瞅：

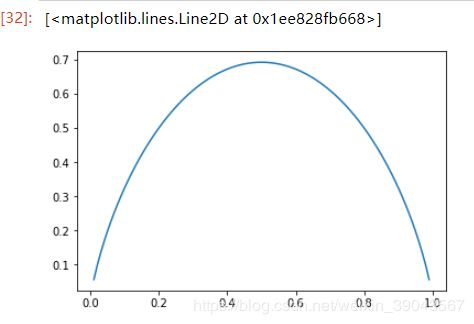
我们以2个类别为例子，则H=-xlog(x)-(1-x)log(1-x)

#定义求信息熵的函数
def entropy(p):
    return -p*np.log(p)-(1-p)*np.log(1-x)
#生成0.01-0.99的x，当作类别所占比例，
x=np.linspace(0.01,0.99,100)
plot.plot(x,entropy(x))

很显然了，p=0.5的时候时，信息熵取到最大值，即两个类别比例各占一半时，不确定度最大。一个类别很少，另外一个类别很多的时候更偏向某一类，确定性很高。

那么，每个节点在哪个维度上划分，某个维度上的哪个值进行划分？

叶子节点的信息熵为0，因为只有一类。所以我们要找每个节点熵的某个维度，在这个维度熵的一个阈值，对数据进行划分，划分后信息熵和其他维度、阈值对应的信息熵比较，取小的!!计划分后是的信息熵降低

如何划分？对所有划分的可能性搜索！

利用信息熵寻找最优划分

利用基尼系数寻找最优划分

基尼系数速度优于信息熵，sklearn默认基尼系数，二者没有明显的效果优劣。

 

 

决策树的局限性：

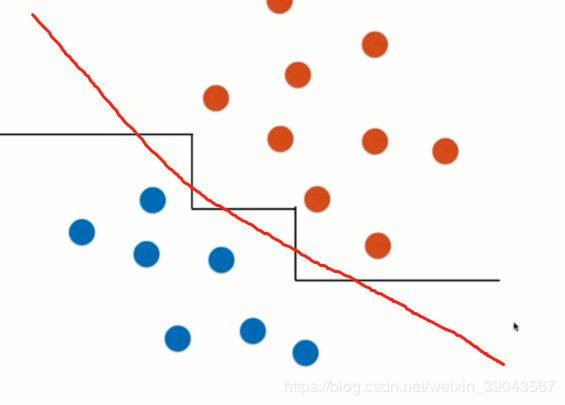
通过上边的决策树的决策边界相信你已经发现，决策边界都是横平竖直的，因为每次都是在某个维度的某个阈值分隔的，所以都是平行于x轴或者y轴。

对于这种情况，可能红色的是好的决策边界，但是决策树只能产生图中折线形式的决策边界。

对个别的数据点很敏感，高度依赖调参。随机森林能够好的发挥决策树的优点。