论文笔记:Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles
Balaji Lakshminarayanan Alexander Pritzel Charles Blundell DeepMind
{balajiln,apritzel,cblundell}@google.com
提出问题
1. 神经网络容易产生过于自信的预测,而错误预测的代价不可接受,必须要估计不确定度。
2. 让网络知道自己知道什么。在领域外预测(out-of-distribution)输出高预测不确定性。
现有办法
- 贝叶斯后验估计
最大后验估计中引入了先验概率(先验分布属于贝叶斯学派引入的,像L1,L2正则化就是对参数引入了拉普拉斯先验分布和高斯先验分布)。
- 拉普拉斯近似
由于没法直接求解 p ( w ∣ t , X ) p(w|t,X) p(w∣t,X),转而求解 g ( w ; X , t , σ 2 ) g(w;X,t,\sigma^2) g(w;X,t,σ2),拉普拉斯近似就是首先假设函数 l o g ( g ( w ; X , t , σ 2 ) ) log(g(w;X,t,\sigma^2)) log(g(w;X,t,σ2))服从高斯分布,然后通过泰勒展开公式, g ( w ; X , t , σ 2 ) ≈ g ( w ^ ; X , t , σ 2 ) − v 2 ( w − w ^ ) 2 g(w;X,t,\sigma^2) \approx g(\hat{w};X,t,\sigma^2)- \frac {v} {2}{(w-\hat{w}^)}^2 g(w;X,t,σ2)≈g(w^;X,t,σ2)−2v(w−w^)2,也就求得了后验概率 p ( w ∣ t , X ) p(w|t,X) p(w∣t,X)的分布。
- MCMC
MCMC方法是使用马尔科夫链的蒙特卡洛积分,其基木思想是:构造一条Markov链,使其平稳分布为待估参数的后验分布,通过这条马尔科夫链产生后验分布的样本,并基于马尔科夫链达到平稳分布时的样本(有效样本)进行蒙特卡洛积分。
- 变分推断
变分推断简单来说便是需要根据已有数据推断需要的分布P;当P不容易表达,不能直接求解时,可以尝试用变分推断的方法。即寻找容易表达和求解的分布Q,当Q和P的差距很小的时候,Q就可以作为P的近似分布代替P。
- 假设滤波
根据点过程理论, 随机集X 在物理空间上可等价的表示为 ∑ x ∈ X ∑x∈X ∑x∈X, δ x δx δx为中心在x的Dirac δ \delta δ函数。PHD滤波是多目标Bayes滤波的近似算法, 它在每个时间点上传播的不是多目标后验密度, 而是后验密度的一阶矩(后验强度函数), 从而降低计算复杂度。
- 期望传播
我们的每个因子都是和θ(整个潜变量和模型参数的集合)有关的,当我们假设每个因子只和θ的一些子集有关时,EP算法其实就是概率图模型(PGM)中的Loopy belief propagation算法。
- MC dropout
在训练的时候,MC dropout 表现形式和 dropout 没有什么区别,按照正常模型训练方式训练即可。MC 体现在我们需要对同一个输入进行多次前向传播过程,这样在 dropout 的加持下可以得到“不同网络结构”的输出,将这些输出进行平均和统计方差,即可得到模型的预测结果及 uncertainty。
本文贡献
-
描述了一个简单的和可扩展的方法来估计神经网络的预测不确定性估计。主张使用合适的得分规则作为训练准则来训练概率神经网络(即模型预测分布)。
-
研究了ensemble和adversarial training的修改对pipeline的影响。
-
提出了一系列评估预测不确定性估计质量的任务,在校准和推广方面的未知类的监督式学习问题。比MC dropout性能好,相比传统方法计算更简单。
整体方案
贝叶斯平均(BMA)假设
最小化NLL准则
对抗训练平滑预测不确定性
集成方法训练和预测
深度神经网络是黑盒预测器,并在诸多领域中应用。当前的贝叶斯方法通过学习权重是目前最好的办法,但训练难度大。本文提出了替代性方案来量化预测不确定性。通过提出校正的uncertainty estimates,dataset shift,不管在已知还是未知的分布上展现了良好的性能。最后讨论该方法在ImageNet的扩展性。

实验
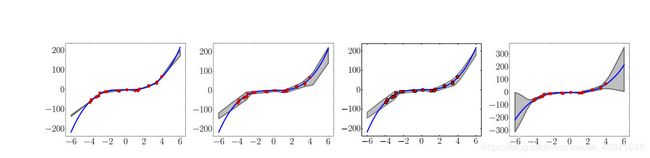
Regression on toy datasets
y = x 3 + ϵ , ϵ ∈ N ( 0 , 3 2 ) y=x^3 + \epsilon, \epsilon ∈ N(0,3^2) y=x3+ϵ,ϵ∈N(0,32)
Regression on real world datasets
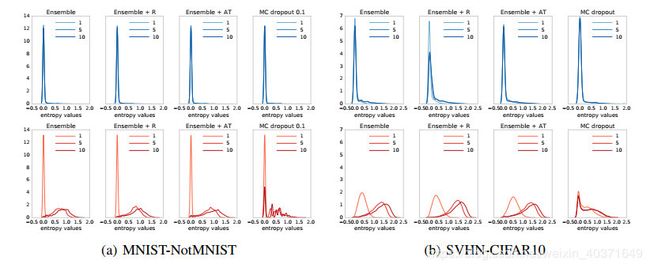
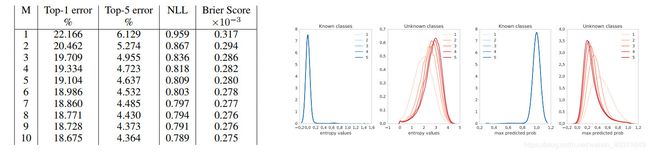
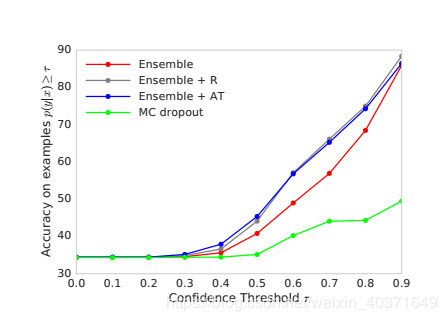
Classification on MNIST, SVHN and ImageNet
Uncertainty evaluation: test examples from known vs unknown classes
讨论
- 提供了预测不确定性的非贝叶斯方法的baseline,鼓励社区考虑非贝叶斯方法,达到与贝叶斯方法类似的效果。
- 用对抗训练处理out-of-distribution 和 Robustness只需少量超参数,可以训练大规模的数据集,非常方便地应用到MLP,CNNs,residual networks。
未来工作
-
专注于训练独立网络,可以更好地并行
-
优化权重,知识的适度混合
-
通过multiple heads,snapshot ensembles, swapout共享参数