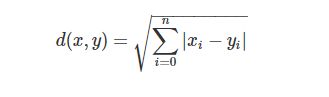KNN_Dense sift_图像识别

KNN

k邻近算法( k-nearest neighbors )，即 KNN 算法

概述

Cover 和 Hart 在 1968 年提出了最初的邻近算法，用于解决分类( classification )的问题。关于这个算法在百度百科中也有介绍:https://baike.baidu.com/item/邻近算法/1151153?fr=aladdin 。

KNN是一种基于实例学习( instance-based learning )，或者所是将所有计算推迟到分类之后的惰性学习( lazy learning)的一种算法，KNN是所有机器学习算法中最简单算法之一。

算法说明

KNN算法的思路是: 如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。通常 K 的取值比较小，不会超过 20。

算法步骤为：

• 计算未知实例到所有已知实例的距离；
• 选择参数 K；
• 根据多数表决( majority-voting )规则，将未知实例归类为样本中最多数的类别。

距离的衡量方法

关于距离的测量方式有多种，这里只介绍两种。

欧拉距离
这种测量方式就是简单的平面几何中两点之间的直线距离。

 

 

并且这种方法可以延伸至三维或更多维的情况。它的公式可以总结为:

曼哈顿距离
顾名思义，城市街区的距离就不能是点和点的直线距离，而是街区的距离。如棋盘上也会使用曼哈顿距离的计算方法：

K 值的选择

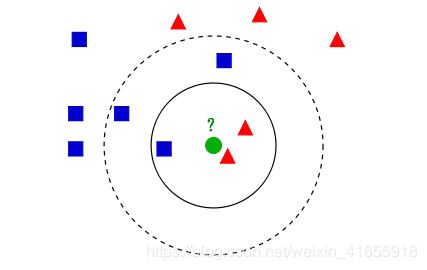
K值的选择会影响结果，有一个经典的图如下:

图中的数据集是良好的数据，即都打好了 label ，一类是蓝色的正方形，一类是红色的三角形，那个绿色的圆形是待分类的数据。

• 1. = 3 时，范围内红色三角形多，这个待分类点属于红色三角形。
• 1. = 5 时，范围内蓝色正方形多，这个待分类点属于蓝色正方形。

如何选择一个最佳的K值取决于数据。一般情况下，在分类时较大的 K 值能够减小噪声的影响，但会使类别之间的界限变得模糊。因此 K 的取值一般比较小 ( K < 20 )。

 

改进

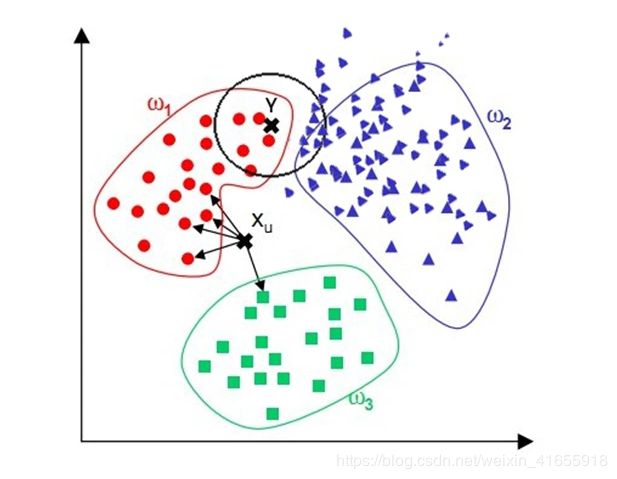
在下面一种情况中：

在点Y的预测中，改范围内三角形分类数量占优，因此将Y点归为三角形。但是从视觉上观测，应该是分为圆形分类更为合理。根据这种情况就在距离测量中加上权重，比如 1/d (d: 距离)。

KNN 的优缺点

优点：

• 简单，易于理解，无需建模与训练，易于实现；
• 适合对稀有事件进行分类；
• 适合与多分类问题，例如根据基因特征来判断其功能分类，kNN比SVM的表现要好。

缺点：

• 惰性算法，内存开销大，对测试样本分类时计算量大，性能较低；
• 可解释性差，无法给出决策树那样的规则。

 

n=10

n=200

n=2000

 

生成数据代码：

# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *

# create sample data of 2D points
n = 200
# two normal distributions
class_1 = 0.6 * randn(n,2)
class_2 = 1.2 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_normal.pkl', 'w') as f:
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
# normal distribution and ring around it
print ("save OK!")
class_1 = 0.6 * randn(n,2)
r = 0.8 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_ring.pkl', 'w') as f:
with open('points_ring_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
print ("save OK!")

进行分类 

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()



# load 2D points using Pickle
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # load test data using Pickle
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
    # test on the first point
    print (model.classify(class_1[0]))

    #define function for plotting
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # lot the classification boundary
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
show()

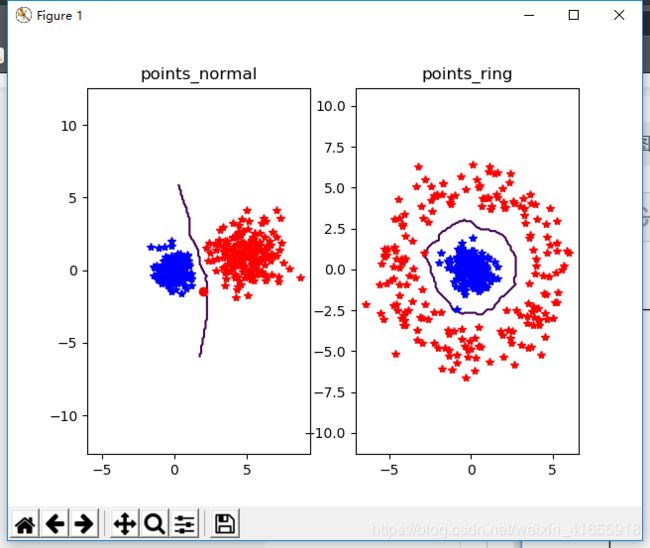
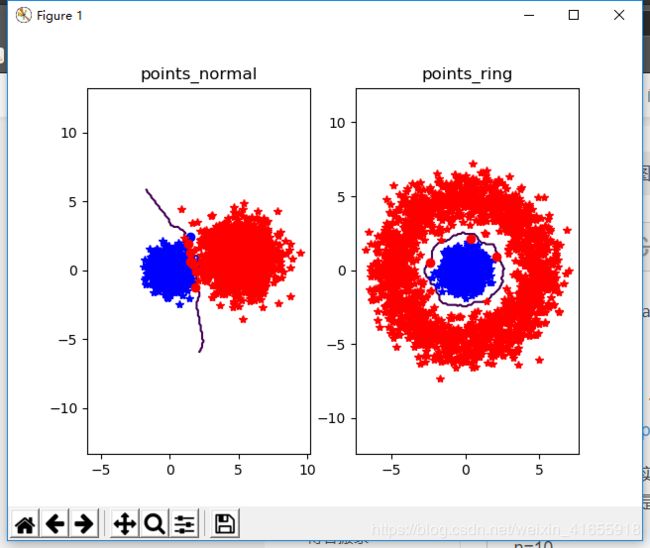
结果分析：
数据数量太少 效果不好，随着数量的增加，效果变好  但时间也变长

Dense sift

DenseSift是Sift的一种变种，其每个描述子也是一个128维的向量，表征的是关键点2邻域内16个像素点沿八个方向的梯度变化，因此维度为16*8=128。它与Sift最大的不同在于关键点的选取是稠密且同规格的，如下图所示。

实例

dsift.process_image_dsift('gesture/empire.jpg','empire.dsift',90,90,True)

 dsift.process_image_dsift('gesture/empire.jpg','empire.dsift',90,40,True)

 

 dsift.process_image_dsift('gesture/empire.jpg','empire.dsift',40,40,True)

# -*- coding: utf-8 -*-
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

dsift.process_image_dsift('gesture/empire.jpg','empire.dsift',90,40,True)
l,d = sift.read_features_from_file('empire.dsift')
im = array(Image.open('gesture/empire.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()

 

# -*- coding: utf-8 -*-
import os
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

imlist=['gesture/example/C-uniform01.ppm','gesture/example/B-uniform01.ppm',
        'gesture/example/O-uniform01.ppm','gesture/example/Five-uniform01.ppm',
        'gesture/example/Point-uniform01.ppm','gesture/example/V-uniform01.ppm']


figure()
for i, im in enumerate(imlist):
    print im
    dsift.process_image_dsift(im,im[:-3]+'dsift',10,5,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')
    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-14]
    subplot(2,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

 

 

手势识别

 

# -*- coding: utf-8 -*-
from PCV.localdescriptors import dsift
import os
from PCV.localdescriptors import sift
from pylab import *
from PCV.classifiers import knn

def get_imagelist(path):
    """    Returns a list of filenames for
        all jpg images in a directory. """

    return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.ppm')]

def read_gesture_features_labels(path):
    # create list of all files ending in .dsift
    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    # read the features
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)
    # create labels
    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # confusion matrix
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print 'Confusion matrix for'
    print classnames
    print confuse

filelist_train = get_imagelist('gesture/train')
filelist_test = get_imagelist('gesture/test')
imlist=filelist_train+filelist_test

# process images at fixed size (50,50)
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))

features,labels = read_gesture_features_labels('gesture/train/')
test_features,test_labels = read_gesture_features_labels('gesture/test/')
classnames = unique(labels)

# test kNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# accuracy
acc = sum(1.0*(res==test_labels)) / len(test_labels)
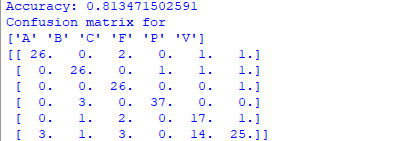
print 'Accuracy:', acc

print_confusion(res,test_labels,classnames)