卷积神经网络CNN的前向和后向传播（一）

原文 Forward And Backpropagation in Convolutional Neural Network地址： https://medium.com/@2017csm1006/forward-and-backpropagation-in-convolutional-neural-network-4dfa96d7b37e 在墙外，在这写是为了方便大家参考。

下面的文章演示了卷积运算在CNN中进行反向传播的过程。

卷积运算与相关的区别

让我们考虑卷积层中的输入和卷积核（也称之为滤波器）。简单起见，$channel$=1，输入矩阵$X$为3x3，卷积核$F$为2x2，$padding=0,stride=1$。前向传播为卷积过程。

而滤波器矩阵$F$与输入矩阵$X$的相关矩阵$O$如下图所示：

卷积核与输入图像的卷积相当于将卷积核旋转180度（先水平翻转再垂直翻转），然后与输入矩阵进行相关操作：

由此可见，卷积运算与相关运算是一样的，只不过是和旋转后的卷积核进行相关运算。

卷积运算的正向和反向传播

注意: 为了方便推导出卷积核的值和输入矩阵值的梯度方程，我们将考虑卷积运算和相关运算看作是一样的，这只是为了处理上简单的考虑。
因此，卷积操作可以用下图来表示：

注意此处为了方便，$F$没有进行180度翻转，因此这里卷积和相关是一样的。
可以用下面的图来进行可视化。

现在，我们要计算卷积核 $F$ 相对于误差 $E$ 的梯度，要解以下的方程。

$$\frac{\partial E}{F_{11}}=\frac{\partial E}{O_{11}}\cdot \frac{\partial O_{11}}{F_{11}}+\frac{\partial E}{O_{12}}\cdot \frac{\partial O_{12}}{F_{11}}+\frac{\partial E}{O_{21}}\cdot \frac{\partial O_{21}}{F_{11}}+\frac{\partial E}{O_{22}}\cdot \frac{\partial O_{22}}{F_{11}}$$

$$\frac{\partial E}{F_{12}}=\frac{\partial E}{O_{11}}\cdot \frac{\partial O_{11}}{F_{12}}+\frac{\partial E}{O_{12}}\cdot \frac{\partial O_{12}}{F_{12}}+\frac{\partial E}{O_{21}}\cdot \frac{\partial O_{21}}{F_{12}}+\frac{\partial E}{O_{22}}\cdot \frac{\partial O_{22}}{F_{12}}$$

$$\frac{\partial E}{F_{21}}=\frac{\partial E}{O_{11}}\cdot \frac{\partial O_{11}}{F_{21}}+\frac{\partial E}{O_{12}}\cdot \frac{\partial O_{12}}{F_{21}}+\frac{\partial E}{O_{21}}\cdot \frac{\partial O_{21}}{F_{21}}+\frac{\partial E}{O_{22}}\cdot \frac{\partial O_{22}}{F_{21}}$$

$$\frac{\partial E}{F_{22}}=\frac{\partial E}{O_{11}}\cdot \frac{\partial O_{11}}{F_{22}}+\frac{\partial E}{O_{12}}\cdot \frac{\partial O_{12}}{F_{22}}+\frac{\partial E}{O_{21}}\cdot \frac{\partial O_{21}}{F_{22}}+\frac{\partial E}{O_{22}}\cdot \frac{\partial O_{22}}{F_{22}}$$

这一些等式也等同于
$$\frac{\partial E}{F_{11}}=\frac{\partial E}{O_{11}}\cdot X_{11}+\frac{\partial E}{O_{12}}\cdot X_{11}+\frac{\partial E}{O_{21}}\cdot X_{11}+\frac{\partial E}{O_{22}}\cdot X_{11}$$

$$\frac{\partial E}{F_{12}}=\frac{\partial E}{O_{11}}\cdot X_{12}+\frac{\partial E}{O_{12}}\cdot X_{12}+\frac{\partial E}{O_{21}}\cdot X_{12}+\frac{\partial E}{O_{22}}\cdot X_{12}$$

$$\frac{\partial E}{F_{21}}=\frac{\partial E}{O_{11}}\cdot X_{21}+\frac{\partial E}{O_{12}}\cdot X_{21}+\frac{\partial E}{O_{21}}\cdot X_{21}+\frac{\partial E}{O_{22}}\cdot X_{21}$$

$$\frac{\partial E}{F_{22}}=\frac{\partial E}{O_{11}}\cdot X_{22}+\frac{\partial E}{O_{12}}\cdot X_{22}+\frac{\partial E}{O_{21}}\cdot X_{22}+\frac{\partial E}{O_{22}}\cdot X_{22}$$

如果我们仔细看，这个等式可以写成卷积操作的形式：

类似地，我们可以得到输入矩阵 $X$ 相对于误差 $E$ 的梯度值：

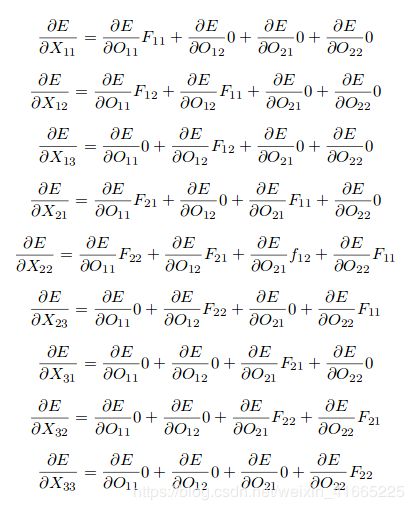
为了得到输入矩阵的梯度$\partial E/\partial X$，我们需要将卷积核旋转180度，通过输出的误差梯度$\partial E/\partial O$计算旋转卷积核 $F$ 的全卷积，如下图所示。

全卷积可以想象为执行如下图所示的过程。

因此，卷积运算就可以实现卷积层的正向传播和反向传播。

要计算池化层和Relu层的梯度，可以通过使用导数的链式法则来计算。