数组全排列问题详解

问题

给定一个集合$S$，输出集合元素的全排列，例如，当$S$=(1,2,3)时，全排列为(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), and (3,2,1).

分析与设计

全排列问题是求一个集合中所有元素不重复的排列结合，因此属于穷举法问题。但是问题的关键是如何不重复的进行列举。实际上，此问题我们可以理解为一个树的遍历问题。如下图所示，对于集合[1,2,3]，可以建立以下的树。

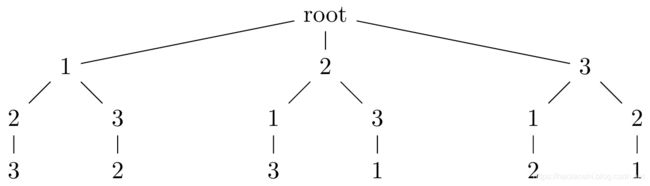
对于只有3个元素的集合，生成的全排列树的第一级有3种可能，第二级是2种，第三级是1种。所以，对于数量为 $n$ 的集合，树的总节点数是 $n!$ 。通过附录算法1，我们可以构建这样的树。

当树完成以后，再利用树的遍历进行一次完全遍历，记录路径信息，则每一个单独的路径上的值的序列即是一个不重复的排列，所有路径的集合即是数组的全排列。

我们可以用一个输入列表 inList 表示输入数据，然后对所有的可能抽取位置，每次从中取一个元素追加到另一个辅助列表 auxList 末尾。如果 inList 不为空，则继续递归计算；否则，在 auxList 中则为排列结合。抽取测试完一种情况后，再将这个元素返回。为一更好地了解整个过程，可以以树型表示，如下图所示。

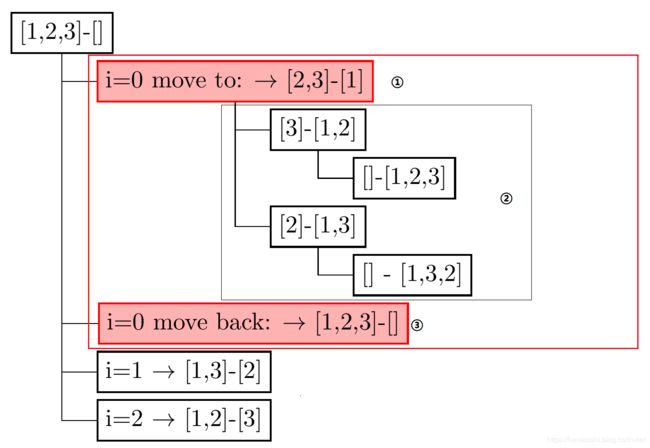
注：以上绘制代码可以在找到 Latex学习笔记 (Ex2) 使用LaTeX画规则的树形图.
在图中所示，对初始化数组 inList 和 auxList 以中括号表示，使用横杠连接。在红色方框内，为 i = 0，即对1个元素进行操作的情况。这时，有三步操作：

• ① 移动第0个元素，可以得到 [2,3] - [1]
• ② 对新的组合调用遍历，这时有两种情况分别是 [1,2,3] 和 [1,3,2] 进行输出
• ③ 将第1个元素移回，以方便下一步（即 i = 1) 的操作。
  这样通过递归遍历，即可实现对数据的全排列输出。

实现代码

/**
 * 使用递归输出 inList 中的元素的全排列，auxList为辅助数据。
 * @param inList 输入列表。
 * @param auxList 辅助列表。
 */
static void traverse(ArrayList<Integer> inList, ArrayList<Integer> auxList) {
	if (inList.size() > 0) { // inList 中有元素，元素递归没有结束，继续递归。
		for (int i = 0; i < inList.size(); i++) {
			auxList.add(inList.remove(i)); // 将 inList 中第 i 个元素添加至 auxList 末尾
			traverse(inList, auxList); // 递归调用变化后的数组情况
			inList.add(i, auxList.remove(auxList.size() - 1)); // 再将这个元素归还给 inList.
		}
	} else { // inList 中元素为空，表示已经全部排列，输出结果。
		System.out.println(Arrays.toString(auxList.toArray()));
	}
}

测试

测试代码：
traverse(new ArrayList(Arrays.asList(1, 2, 3, 4, 5)), new ArrayList());
结果：

[1, 2, 3, 4]
[1, 2, 4, 3]
[1, 3, 2, 4]
[1, 3, 4, 2]
[1, 4, 2, 3]
[1, 4, 3, 2]
[2, 1, 3, 4]
[2, 1, 4, 3]
[2, 3, 1, 4]
[2, 3, 4, 1]
[2, 4, 1, 3]
[2, 4, 3, 1]
[3, 1, 2, 4]
[3, 1, 4, 2]
[3, 2, 1, 4]
[3, 2, 4, 1]
[3, 4, 1, 2]
[3, 4, 2, 1]
[4, 1, 2, 3]
[4, 1, 3, 2]
[4, 2, 1, 3]
[4, 2, 3, 1]
[4, 3, 1, 2]
[4, 3, 2, 1]

附1：完全树的生成算法

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class Node {
	
	public static void main(String[] args) { 
		Node root = Node.createTree(new int[]{1,2,3});
		System.out.println(root);
	} 
	
	// 
	public Node parent;
	public int data;
	public List<Node> nodes = new ArrayList<Node>();
	public int[] values = new int[0]; 

	public static Node createTree(int[] array) {
		Node root = new Node();
		root.values = array;
		Stack<Node> stack = new Stack<Node>();
		stack.push(root);

		while (stack.size() > 0) {
			Node node = stack.pop();
			for (int i = 0; i < node.values.length; i++) {
				Node child = new Node();
				child.data = node.values[i];
				child.parent = node;
				child.values = new int[node.values.length - 1];
				for (int j = 0; j < child.values.length; j++)
					child.values[j] = node.values[j < i ? j : j + 1];
				node.nodes.add(child);
				stack.push(child);
			}
		}

		return root;
	}
}