学习吴恩达卷积神经网络个人笔记（1）

1.边缘检测示例(进行卷积运算convolution operation)

在数学中星号就是卷积的标准标志，但在python中常用来表示乘法或者元素乘法，所以有很多定义，它是一个重载符号。所以表示的时候要特别申明它是卷积即“*”=convolution;一般不同编程语言有不同函数来实现convolution而不是用星号来表示。（eg:python(conv_forward)/tensorflow(tf.nn.conv2d)
其实卷积运算就是一个矩阵相乘的过程。例如：

给你一张左边的6x6的图片，然后你用中间的3x3的图片与它相乘就可以得到右边4x4的图片，它是怎么乘的呢，就是从左上至右下用中间的矩阵去套，一个一个相乘再相加得到右边的图。中间的图就是一个核，或者称为过滤器，英文filter。
为什么要这么做呢，下面这张图就很好的诠释了。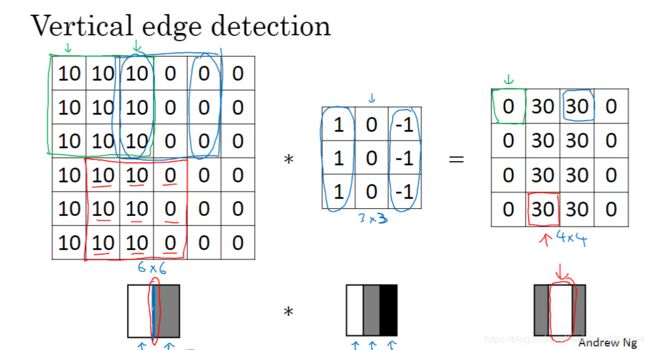
这张图中，很显然，正数为白色，0为灰色，负数为黑色。也就是一个由亮到暗的过程，这样就可以得到一个很明显的垂直边缘。当图片是从暗到亮的图片的时候，得到的效果也不同。这里得到的是由暗变亮的边缘
同样的，有垂直边缘检测自然就有水平边缘检测，如图：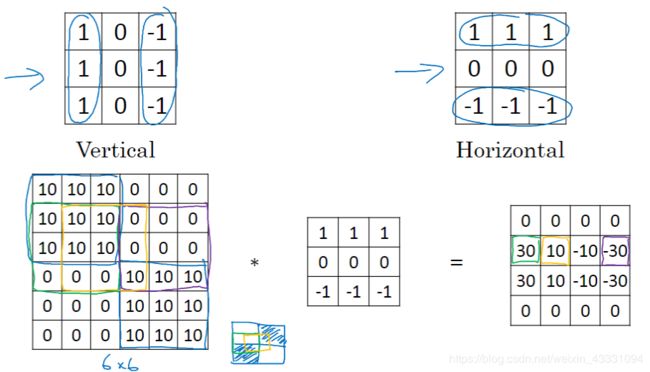
你可能会问，为什么一定是1,0，-1呢，可不可以用其他的数字组合成filter呢，这个问题很多大佬已经研究过，得到的结果就是，以下几种是比较常见的组合,分别是:filter/Sober filer/Scharr filter

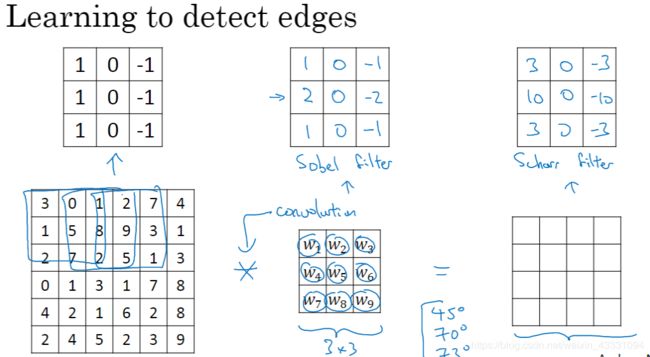
2.padding（填充）

在经过上面的卷积过程你会发现一个问题，那就是你的图片会变小，6x6的图片变成了4x4，这是因为它的计算公式是这样的:假设你的图片为n X n，然后卷积为f X f，那么得到的图片为（n-f+1)X(n-f+1),而且有一个更严重的问题，你会发现图片中间位置被filter多次乘积，但是边沿的位置缺少了很多次乘积，这就意味着边沿的位置信息少了很多。如何解决这个，那就要用到填充，在图片周围填充一层就可以得到一个8X8的图片然后再卷积来得到一个和原图一样大小的图片了。

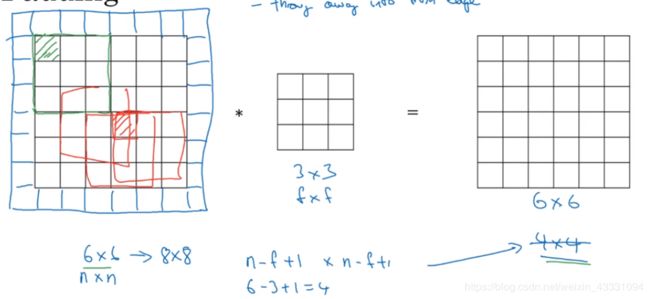
当然你也可以再填充不断增大，我们把填充的层数设为p，那么我们得到的图片大小就是（n+2p-f+1) X（n+2p-f+1)，一般我们有两种filter，一种叫Valid,顾名思义就是不填充，也就是p等于0.另外一种是Same，填充的层数为p，至于p为多大就看你怎么设置了
通常我们的卷积乘积是以步长为1进行的，有时候你可能会以2,3…等为步长进行卷积，这里我们假定步长为s那么我们的到的图片的乘积就是[(n+2p-f)/s+1]X[(n+2p-f)/s+1]在这里又产生一个问题那就是如果[(n+2p-f)/s+1]不是整数怎么办，在这里我们的解决办法就是[(n+2p-f)/s+1]向下取整：


我们在使用过程中为了编程的简洁性，有时候会将卷积核进行翻转来简化编程：

3.卷积（三维）

这里仅仅是二维图像的卷积，也就是灰度图，那么我们扩展到三维图像的卷积，也就是日常的RGB图：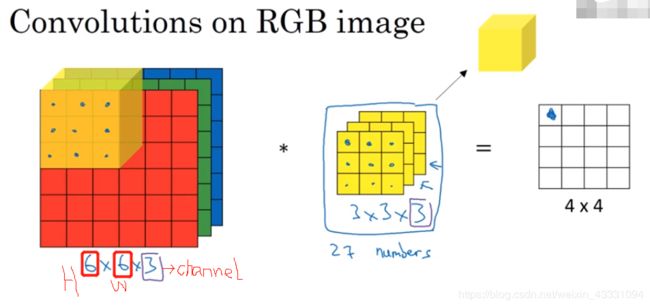
如图，这是一个6X6的3通道图，其中的6分别是高和宽，然后是通道数，这里用一个3X3X3的卷积核进行卷积，卷积方法一样都是对应的数相乘然后相加得到一个数，然后从左上依次往右下得到一个效果图，但是这里需要注意，我们最后得到的是一个4X4X1的二维图也就是单通道图。那么如果你想要只跟R有关的效果图就只需要对G、B这两个通道的卷积核的值设为0或者1即可。如果你想要得到一个RGB三通道图的话，你可以分别卷积然后最后叠加得到你想要的图：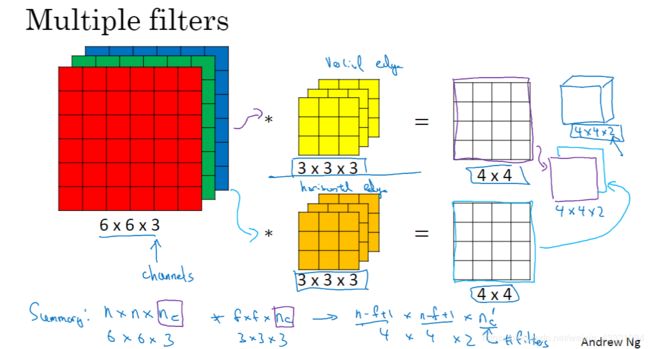

4.卷积网络

我们在得到两个不同的4X4卷积神经网络层(w[1]a[0])后，再通过python的广播机制给它的16个元素加上同一偏差b，然后应用非线性函数，因为它是一个非线性激活函数ReLU所以加上b后所得也是一个4X4的矩阵，然后同样运用叠加就可以得到一个4X4X2的矩阵，这就得到了卷积神经网络的第一层。

避免过拟合：
我们使用的两个卷积核可以由你选择设为3.4.5…等，如果我们设卷积核为10，一个卷积核的参数为27+b也就是28个，那么10个卷积核就有280个参数，这样设定的好处在于你不管图片有多大，1000.10000还是更多你都只需要设置280参数，这就是避免过拟合。

下图是常用的参数变量或者卷积标准：

看下面这张图，我们以39X39X3的矩阵做一个例子，在经过10个3X3X3的卷积核，以步长为1，填充为0得到一个37X37X10的矩阵，然后经过20个5X5X5的卷积核，以步长为2，填充为0得到一个17X17X20的矩阵，依次类推得到不同的效果。

通常称上面的做法叫Convolution也就是第一层卷积网络，但我们经常用到的还有下面的pooing(池化层)以及Fully connected(全连接层)

池化层

：使用池化层是为了缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。池化层主要是最大池化，也有比较少用的平均池化。
顾名思义，最大池化就是把一个卷积核套到矩阵中，然后选取这个卷积所套内的几个数中的最大值，然后这样就可以得到一个和卷积核一样尺寸的矩阵，这个矩阵就可以很好地显示出特征。

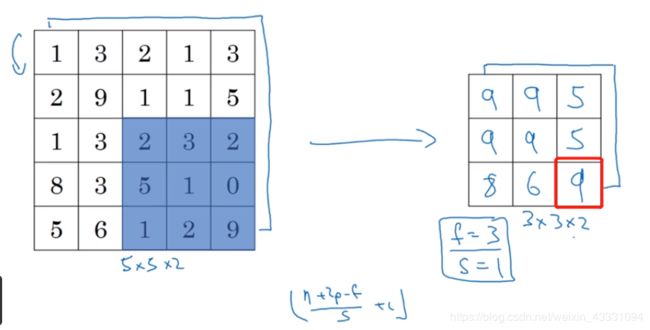
下图是平均池化，道理相同，就是把核套进去里面所有数相加然后求平均值。

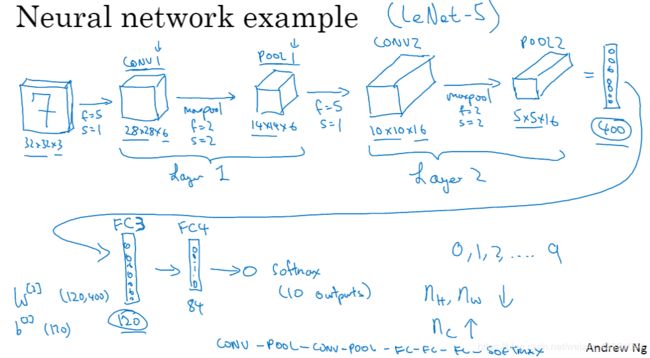
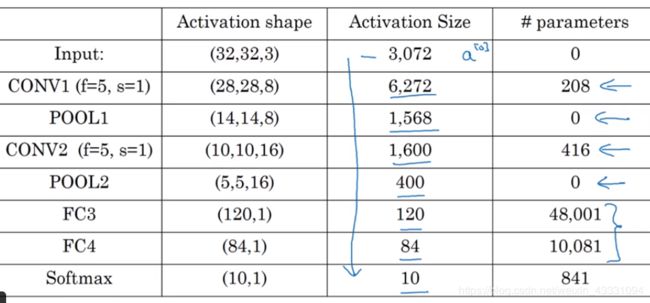
但是池化有一个问题就是核的参数是未定的，得到的也只是里面的最大值，而且卷积层和池化层均是一层的情况，那么这里可以引入Fully connected(FC)“全连接层”，其实我们可以理解为一个FC就是由一个conv加一个pool组成的，例如下图，假设我们要识别一个32X32X3的手写的数字图像，经过一个conv加一个pool后得到一个14X14X6的矩阵，再经过第二个FC(又一个conv加一个pool)后得到5X5X16的矩阵，这个矩阵共有400个元素，它是连接的。然后我们再经过第三个FC，第四个…得到一个softmax的输出然后与我们的设定的softmax进行匹配得出结论，一般我们设定的softmax不要自己设，而应该去看看别人的项目和码源。


#以上是我观看网易云课堂吴恩达卷积神经网络课后的个人笔记，本人大一小白一枚，欢迎批评指正，谢谢！!