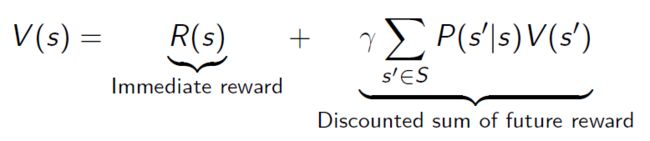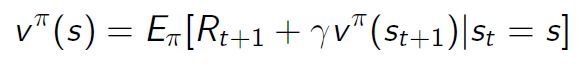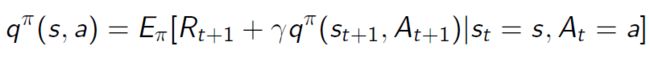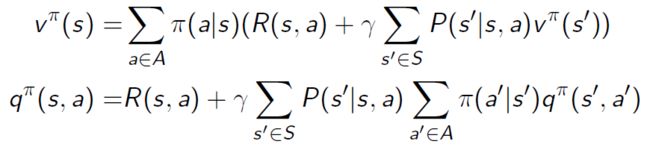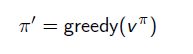2. 强化学习之——马尔科夫决策过程

目录

马尔科夫链

马尔科夫奖励过程（MRP）

马尔科夫决策过程（MDP）

马尔科夫决策过程中的策略估计/预测（policy evaluation/prediction）

马尔科夫决策过程中的预测和控制（prediction and control in MDP）

动态规划

预测（评估一个给定的策略 evaluate a given policy）

控制（寻找最优的策略 search the optimal policy）

---

本次课程核心内容

MDP：马尔科夫决策过程

policy evaluation：给定 policy 怎样去衡量它的价值

MDP 的两种控制方法：

—policy iteration

—value iteration

马尔科夫链

马尔科夫性：未来的转移到的状态跟过去是独立的，它只取决于现在状态

状态转移矩阵 P：（矩阵中每一个元素都是一个概率分布）

马尔科夫链的举例：当从状态 S3 开始时，可以对链进行采样（依据状态转移矩阵），假如说我们规定链的长度，那么就可以得到很多串轨迹（例如下面的三串轨迹），这里轨迹的获得是没有自身动作的，单纯依据上述状态转移矩阵获得（打个比方，就像小船随波逐流一样）

马尔科夫奖励过程（MRP）

马尔科夫奖励过程 = 马尔科夫链 + 奖励

奖励其实是一个期望（当你到某一个状态时预期可以获得多大的奖励）：

再加上一个折扣系数：伽马 γ（目的是避免带环的过程+对环境不确定性表示+对人贪婪行为的模拟）

与马尔科夫链类似，马尔科夫奖励过程 agent 可以看做一个随波逐流的小船，按我们规定的状态转移矩阵的内部概率进行转移

马尔科夫奖励过程举例：（因为状态是有限的，所以可以定义一个状态的奖励函数的矩阵），至于怎么计算值函数  ，在知道 horizon 之后就是进行采样然后求均值就好了呀（这种计算状态值函数的方法其实就是蒙特卡罗采样）

Horizon的定义：一个 epoch 的步数，也就是你马尔科夫链（或者马尔科夫奖励过程）每个链的长度

Reward（奖励）的定义：某一个状态所获得的收益，只针对一个状态本身

Return（回报）的定义：从 t 时刻到轨迹最后把每个状态的奖励进行 γ 次方倍折扣所得到的收益（这里的下标应该是错误的）

State Value function（状态值函数）的定义：从 s 状态开始的轨迹的总回报的期望，说白了就是 return 的期望

回到上面的，求  的问题上，除了上述提到的蒙特卡罗采样模拟的方法，还可以采用贝尔曼方程法进行解决。

贝尔曼方程核心思想就是迭代：当前状态值函数 = 当前奖励 + 下一步每个状态的值函数×转移概率累计求和之后×折扣因子γ

贝尔曼方程的矩阵表示：

回到我们的初衷：用贝尔曼方程求解状态值函数 V，怎么求呢，既然我们都矩阵表示了，那当然就是求上面的矩阵方程的解嘛！矩阵求逆就完了！但是问题来了，高维度的矩阵求逆是在是太复杂了，所以这种方法还只是适合于小型的马尔科夫奖励问题。

解决大型的马尔科夫奖励过程的方法其实也有：1. 动态规划  2. 蒙特卡洛  3. TD算法（结合1和2）

1. 蒙特卡洛采样解决动态大型马尔科夫奖励问题方法：

2. 动态规划的方法解决大型的马尔科夫奖励问题的方法（不断去迭代贝尔曼方程直至状态值函数收敛为止）：

马尔科夫决策过程（MDP）

看上图就知道MDP与上面提到的马尔科夫链和马尔科夫奖励过程的区别了，MDP 其实就是说有个动作 action 去控制它，使得它拿到更多奖励，而 MRP 纯粹就是依据一定的底层动力学规则（如状态转移矩阵）去随波逐流，瞎猫碰死耗子似的去拿奖励。

马尔科夫决策过程对比马尔科夫奖励过程又多了动作这个东西。我们回忆一下，马尔科夫奖励过程相对于马尔科夫链是多了奖励 reward，所以可以看出来这些理论和概念其实就是这么一步步发展过来的。下图标红的地方就是是 MDP 和 MRP 相区别的部分。

1. 多了 action

2. 在状态转移矩阵中，不仅要考虑上一时刻的状态，还要考虑上一时刻的动作

3. 在奖励函数中，不能仅仅考虑一个状态，要结合状态与动作考虑奖励函数

讲动作之前一定要讲这个 policy，也就是策略。什么是 policy 呢？policy 就是决定在某一个状态下应当采取的行为，其实就是一种选择策略。也就是说，给策略函数 policy function 输入一个状态，那么之后就会输出相应的各个行为对应的概率（当然也可能是确定性的动作结果），也就是说这个函数告诉 agent 在遇到某种情况时应该怎么办才能利益最大化，就像古代战争剧里的军师一样。所以说这个策略是十分十分重要的，强化学习的目的也就是想要找到这个军师。

下面我们就一步步来看看怎么找到这个军师，啊不，策略。

马尔科夫决策过程和马尔科夫奖励过程的转换（第一个公式是状态转移方程的转化，第二个公式是奖励函数的转化）

比较下图左边的马尔科夫（奖励）过程与下图右边的马尔科夫决策过程的差异：主要在于是否有那个动作的选择上面，MDP 多了动作层，也就多了动作的决策层。

那么顺着往下走，我们把马尔科夫决策过程的这个状态值函数 state-value function 给它定义下来，其实这里的 MDP 的状态值函数与前面的 MRP 的状态值函数十分类似，唯一的不同之处在于状态值函数定义中。在上面那个 MRD 过程里，是没有动作 a ，也就没有使用策略进行动作选择这一说，所以那里的状态值函数就是单单取决于环境的状态转移矩阵，就像是随波逐流的纸船。而这里MDP 中的状态值函数的定义为：从 s 状态开始的在 π 策略下获得的轨迹总回报的期望，也即有了策略 π 的参与，状态不是随意就转移了：

为了体现动作 a 的作用，在马尔科夫决策过程中，类似于 V 函数，我们又引入了 Q 函数，Q 函数是状态动作值函数 state-action value function，当然了，Q 函数必然也是基于策略 π 的：

那么 V 函数与 Q 函数之间有关系吗？当然有！！！他们两者之间是可以相互转换的。

马尔科夫决策过程中 状态值函数 VS 状态动作值函数（两者之间的转换）

贝尔曼期望方程 V 函数形式（这里 R 的下标应该是t）：

贝尔曼期望方程 Q 函数形式（同上）：

价值值函数V与状态动作值函数Q之间的两个关系：（分别代表了直接转化与贝尔曼方程转化）

上面的两个公式再相互带入就有：

马尔科夫决策过程中状态值函数 V 的 backup diagram（这里可以理解为回溯图的意思，依赖于贝尔曼方程），注意下面的例子公式里面有两层的加和，也就是一层层往上推—— 目的是构造未来 V 函数与当前 V 函数之间的关系

马尔科夫决策过程中状态动作值函数 Q 的 backup diagram——未来 Q 函数与当前 Q 函数之间的关系

马尔科夫决策过程中的策略估计/预测（policy evaluation/prediction）

其实就是给定策略 π 然后评估状态的值：也就是计算获得某一个状态的  

以上面小船的例子，怎么做策略估计？也就是说给定策略 π 怎么计算每一个状态的价值？

情况一：

情况二：

马尔科夫决策过程中的预测和控制（prediction and control in MDP）

动态规划

动态规划可以用来求解马尔科夫决策过程，因为马尔科夫决策过程中贝尔曼方程可以不断进行循环分解

预测（预测就是评估给定的策略 evaluate a given policy）

输入：给定一个马尔科夫决策过程和给定的策略 π 

输出：价值函数 （用于评估）

MDP 中的策略估计：也就是评估当前的 policy 有多大的价值（输出 ），解决方案就是不断去迭代贝尔曼期望方程，直到状态函数不断从 v1 开始直到收敛到 。具体的算法为：

举例：栅格图中评估随机策略的解决方式就是直接上来迭代就好

一个可以动手的小例子：https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_dp.html

每一次运行policy evaluation，每个状态的值就会改变（所有就会给出一个新的value），直至所有的状态的值最终全部收敛不再变化。之后就可以进行策略的更新了（也就是某个状态选择哪个动作）

控制（控制就是寻找最优的策略 search the optimal policy）

输入：只给定一个马尔科夫决策过程

输出：价值函数极大化的情况下就称作是最优价值函数 v* ，此时所采用的策略就是最优策略 π* 

MDP 被解其实就是说获得了最优的值函数 v*

怎么找最优的策略policy？

       1. 如果有Q函数，就可以采用极大化Q函数的方法找到最优policy

         2. 穷举法——太慢了！！！

其中，给定一个有限步长的MDP问题，最优的策略policy是确定的且不随时间变化，但是结果却不一定是唯一的

怎样高效地搜索最优的policy去得到最大的价值函数呢？—— 这就是MDP控制（MDP control）的东西，总共有两种方法：策略迭代和值迭代：

策略迭代（policy iteration）：

策略迭代总共有两步组成并且不断去迭代：

1. 评估策略 π（Evaluate the policy π）：给定current π，然后计算状态值函数 v

2. 策略提升：对状态值函数  采取贪心的算法来 improve policy π（improve the policy π by acting greedily with respect to ）

具体第二步是怎样去 improve policy π 呢？—— 最大化Q函数即可，也就是选择使Q函数最大的状态动作对

这样的贪心的方法一定是单调的提升policy的，其证明如下：

所以说在策略提升结束之后，就会得到一个最佳的策略，采取这个极大化的动作后，Q函数就变成V函数，之后就满足贝尔曼最优方程（只有在最优policy的条件下是满足的）：

贝尔曼最优方程：

"""策略迭代的核心代码，完整代码见文章末尾GitHub链接"""
def policy_iteration(env, gamma = 1.0):
    """ Policy-Iteration algorithm """
    policy = np.random.choice(env.env.nA, size=(env.env.nS))  # initialize a random policy
    max_iterations = 200000
    gamma = 1.0
    for i in range(max_iterations):
        old_policy_v = compute_policy_v(env, policy, gamma)
        new_policy = extract_policy(old_policy_v, gamma)
        if (np.all(policy == new_policy)):
            print ('Policy-Iteration converged at step %d.' %(i+1))
            break
        policy = new_policy
    return policy

值迭代（value iteration）：

值迭代也是基于贝尔曼最优方程推导出来的，只不过值迭代把贝尔曼最优方程转换为 update rule 来进行不断的回溯迭代，整个迭代的过程没有 policy 的参与

1. 迭代找最优值函数：先不断迭代贝尔曼最优方程（就是最大化Q函数）得到最优的 v* 

2. 最佳策略提取过程：用argmax把Q函数重构出来，然后找到那个最大值的action就是他要选择的策略

具体的算法如下： 

"""值迭代的核心代码，完整代码GitHub链接在文章末尾"""
def value_iteration(env, gamma = 1.0):
    """ Value-iteration algorithm """
    v = np.zeros(env.env.nS)  # initialize value-function
    max_iterations = 100000
    eps = 1e-20
    for i in range(max_iterations):
        prev_v = np.copy(v)
        for s in range(env.env.nS):  # 其实这里可见，没有policy的参与，只是不断最大化Q
            q_sa = [sum([p*(r + prev_v[s_]) for p, s_, r, _ in env.env.P[s][a]]) for a in range(env.env.nA)] 
            v[s] = max(q_sa)
        if (np.sum(np.fabs(prev_v - v)) <= eps):
            print ('Value-iteration converged at iteration# %d.' %(i+1))
            break
    return v

还是那个动手的小演示：https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_dp.html可以分别尝试策略迭代和值迭代（这两个最终结果是一致的）

 

 

借用周老师视频下方“鱼丸泡粗面”的评论来再次说明值迭代和策略迭代的关系：

“对于MDP的问题，我的理解是 不论是 value iteration 或者是 policy iteration，其核心都是那个 value function

1. 对于value iteration 在求解最佳 bellman 等式的时候，始终在使用 value function 进行迭代，直到得到一个收敛的最终的 全局 value function，最后从 value function 反推出在每个 state 需要采取怎样的动作才能达到这样的 value function，即policy

2. 对于 policy iteration，相当于在每次进行迭代的时候都会有一个固定的 policy，在全局的 value function 收敛之前，使用这个 policy 一直和环境交互进行迭代。之后得到一个在该policy下的全局 value function，然后用这个 value function 指导 policy，使得在每个state的时候policy向着value function变大的方向做动作。所以，所有的核心都是 value function。”

Homework：https://github.com/cuhkrlcourse/ierg6130-assignment

 

另：文章后面提到的 policy iteration & value iteration 的 python 代码：

          https://github.com/cuhkrlcourse/RLexample/tree/master/MDP

 

注：本文所有内容源自于B站周博磊老师更新完的强化学习纲要课程，听完之后获益很多，本文也是分享我的听课笔记。周老师Bilibili视频个人主页：https://space.bilibili.com/511221970?spm_id_from=333.788.b_765f7570696e666f.2

感谢周老师 :)