算法与数据结构复习 第三章 栈与队列（详解）

第三章 栈与队列

书面作业

一、判断题

1、在对不带头结点的链队列作出队操作时，不会改变头指针的值。 (F)
解析：
会改变，头指针变为相连的指针；

2、循环队列执行出队操作时会引起大量元素的移动。 (F)
解析：
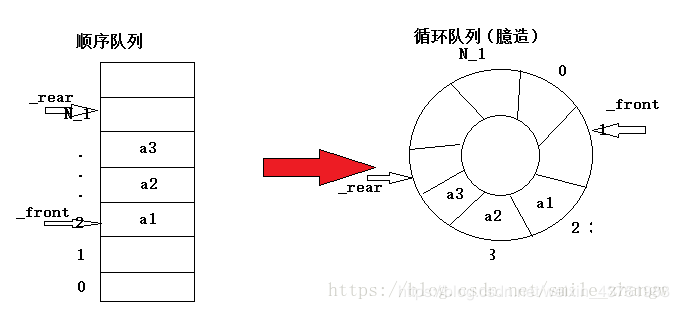循环队列详解；

3、不论是入队列操作还是入栈操作,在顺序存储结构上都需要考虑"溢出"情况。 (T)
解析：
因为存贮空间是有限的；

4、“Circular Queue” is defined to be a queue implemented by a circularly linked list or a circular array. (F)
翻译：
“循环队列”定义为由循环链表或循环数组实现的队列
解析：
循环队列是一个抽象的概念，不局限于实现方式。也就是说，可以可以用各种数据结构实现；

5、n个元素进队的顺序和出队的顺序总是一致的。 (T)
解析：

• 先进者先出，就是"队列" 我们可以想象成，排队买票，先来的先买，后来的只能在末尾，不允许插队。
• 队列的两个基本操作：
  • 入队 将一个数据放到队列尾部；
  • 出队 从队列的头部取出一个元素。
• 队列也是一种操作受限的线性表数据结构 它具有先进先出的特性，支持队尾插入元素，在队头删除元素。

队列详解

6、队列和栈都是运算受限的线性表，只允许在表的两端进行运算。 (F)
解析：
栈只允许在栈顶操作；

7、队列是一种插入和删除操作分别在表的两端进行的线性表，是一种先进后出的结构。 (F)
解析：
队形是一中先进先出的结构；

8、若用data[1…m]表示顺序栈的存储空间，则对栈的进栈、出栈操作最多只能进行m次。 (F)
解析：
可以进行无限次，只要数组没溢出；

9、在用数组表示的循环队列中，front值一定小于等于rear值。 (F)
解析：
详解请看判断题第二题；

10、循环队列也存在着空间溢出问题。 (T)
解析：
循环队列的存储空间也是有限的；

11、通过对堆栈 S 操作：Push(S,1), Push(S,2), Pop(S), Push(S,3), Pop(S), Pop(S)。输出的序列为：123。 （F）
解析：
模拟

0	1	2	3	4	5	6	7	8

Push(S,1)

0	1	2	3	4	5	6	7	8
1

Push(S,2)

0	1	2	3	4	5	6	7	8
1	2

Pop(S)

0	1	2	3	4	5	6	7	8
1

输出：2
Push(S,3)

0	1	2	3	4	5	6	7	8
1	3

Pop(S), Pop(S)
输出：31
总输出的序列为：231

12、栈是插入和删除只能在一端进行的线性表；队列是插入在一端进行，删除在另一端进行的线性表。 （T）
解析：
栈和队列详解；

13、若一个栈的输入序列为{1, 2, 3, 4, 5}，则不可能得到{3, 4, 1, 2, 5}这样的出栈序列。 （T）
解析：
1一定在2的后面；

14、栈和队列的存储方式，既可以是顺序方式，也可以是链式方式。 （T）

15、An algorithm to check for balancing symbols in an expression uses a stack to store the symbols. （T)
翻译：
检查表达式中平衡符号的算法使用堆栈来存储符号。
解析：
栈的应用之检测平衡符号;(即中缀转后缀表达式）

二、单选题

1、为解决计算机主机与打印机之间速度不匹配问题，通常设置一个打印数据缓冲区，主机将要输出的数据依次写入该缓冲区，而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是？ (B)

1. 堆栈
2. 队列
3. 树
4. 图

解析：
分析题目中的数据是具有“先进后出”还是“先进先出”特性，再判断其逻辑结构为栈或者队列。由于本题中先进入打印数据缓冲区的文件先被打印，因此打印数据缓冲区具有先进先出性，则它的逻辑结构应该是队列；

2、利用大小为n的数组（下标从0到n-1）存储一个栈时，假定栈从数组另一头开始且top==n表示栈空，则向这个栈插入一个元素时，修改top指针应当执行： (C )

1. top=0
2. top++
3. top–
4. top不变

解析：
top==n表示栈空，栈反过来；

3、Suppose that all the integer operands are stored in the stack S1, and all the operators in the other stack S2. The function F() does the following operations sequentially:

• (1) Pop two operands a and b from S1;
• (2) Pop one operator op from S2;
• (3) Calculate b op a; and
• (4) Push the result back to S1.

Now given { 5, 8, 3, 2 } in S1(where 2 is at the top), and { *, -, + } in S2 (where + is at the top). What is remained at the top of S1after F() is executed 3 times? ()

1. -15
2. 15
3. -20
4. 20

翻译：
假设所有整数操作数都存储在堆栈S1中，而所有运算符都存储在另一个堆栈S2中。函数F（）按顺序执行以下操作：

• 从S1弹出两个操作数a和b；

• 从S2弹出一个运算符op；

• 计算b op a；以及

• 将结果推回到S1。

现在给定S1中的{5，8，3，2}（其中2在顶部），以及S2中的{*，-，+}（其中+在顶部）。在执行了3次F（）之后，S1顶部还剩下什么？(B)

1. -15
2. 15
3. -20
4. 20

解析：

S1:

0	1	2	3
5	8	3	2

S2:

0	1	2	3
*	-	+

第一次执行F()函数

• S1弹出 a=2,b=3;
• S2弹出 op = +;
• 3+2=5;
• 5压入S1；

S1:

0	1	2	3
5	8	5

S2:

0	1	2	3
*	-

第二次执行F()函数

• S1弹出 a=5,b=8;
• S2弹出 op = -;
• 8-5=3;
• 3压入S1；

S1:

0	1	2	3
5	3

S2:

0	1	2	3
*

第三次执行F()函数

• S1弹出 a=3,b=5;
• S2弹出 op = *;
• 5*3=15;
• 15压入S1；

S1:

0	1	2	3
15

S2:

0	1	2	3

S1剩下15；

4、栈的插入和删除操作在（A）进行。

1. 栈顶
2. 栈底
3. 任意位置
4. 指定位置

5、若采用带头、尾指针的单向链表表示一个堆栈，那么该堆栈的栈顶指针top应该如何设置？ (A)

1. 将链表头设为top
2. 将链表尾设为top
3. 随便哪端作为top都可以
4. 链表头、尾都不适合作为top

6、若用大小为6的数组来实现循环队列，且当前front和rear的值分别为0和4。当从队列中删除两个元素，再加入两个元素后，front和rear的值分别为多少？ (A)

1. 2和0
2. 2和2
3. 2和4
4. 2和6

7、Among the following statements about stacks, the FALSE ones are: (C )

1. A stack has to be used to rewrite a recursive function iteratively.
2. Some information must be stored in a system stack when a function call is made.
3. The popping order must be uniquely determined by the order of pushing the elements into a stack.
4. Stack is a kind of restricted linear list, where operations are allowed at both of its ends.

A. 1 only
B. 1, 2 and 3
C. 1, 3 and 4
D. 2, 3 and 4
翻译：
在以下关于堆栈的语句中，错误的语句是：ACD

1. 必须使用堆栈迭代重写递归函数。
2. 函数调用时，某些信息必须存储在系统堆栈中。
3. 弹出顺序必须由将元素推入堆栈的顺序唯一确定。
4. 堆栈是一种受限的线性列表，它的两端都允许操作。

8、表达式a*(b+c)-d的后缀表达式是： (A)

1. a b c + * d -
2. a b c d * + -
3. a b c * + d -
4. - + * a b c d

解析：
步骤

• 当输入的是操作数时，直接输出a;
• 遇到操作符，如果栈为空入栈，*入栈

0	1	2	3
*

• 当输入的是开括号时，把它压栈;

0	1	2	3
*	(

• 当输入的是操作数时，直接输出b;
• 当输入的是运算符，因为栈顶是开括号，+ 压栈；

0	1	2	3
*	(	+

• 当输入的是操作数时，直接输出c;
• 当输入的是闭括号时，把栈中的元素依次弹出，直到遇到第一个开括号为止，输出+；

0	1	2	3
*

• 当输入的是运算符，栈顶运算符的优先级不低于输入的运算符的优先级，将栈顶元素弹出，把输入的运算符op 压栈；栈顶元素*的优先级大于-的优先级，输出*，- 压栈;

0	1	2	3
-

• 当输入的是操作数时，直接输出d;
• 最后，当中缀表达式中的符号序列全部读入时，若栈内仍有元素，把它们全部依次弹出；输出-；

总输出：a b c + * d -;

9、循环顺序队列中是否可以插入下一个元素（A）。

1. 与队头指针和队尾指针的值有关
2. 只与队尾指针的值有关，与队头指针的值无关
3. 只与数组大小有关，与队首指针和队尾指针的值无关
4. 与曾经进行过多少次插入操作有关

解析：
当队头指针等于队尾指针时，队列满；

10、若已知一队列用单向链表表示，该单向链表的当前状态（含3个对象）是：1->2->3，其中x->y表示x的下一节点是y。此时，如果将对象4入队，然后队列头的对象出队，则单向链表的状态是： (B)

1. 1->2->3
2. 2->3->4
3. 4->1->2
4. 答案不唯一

11、判断一个循环队列QU（最多元素为MaxSize）为空的条件是（A）。

1. QU.front == QU.rear
2. QU.front != QU.rear
3. QU.front == (QU.rear + 1) % MaxSize
4. QU.front != (QU.rear + 1) % MaxSize

解析：
QU.front = = QU.rear 或者 (QU.front +1)% MaxSize= = (QU.rear + 1) % MaxSize;

12、设栈S和队列Q的初始状态均为空，元素{1, 2, 3, 4, 5, 6, 7}依次进入栈S。若每个元素出栈后立即进入队列Q，且7个元素出队的顺序是{2, 5, 6, 4, 7, 3, 1}，则栈S的容量至少是： (D)

1. 1
2. 2
3. 3
4. 4

解析：
S:

0	1	2	3	4	5	6	7
1	2

Q:

0	1	2	3	4	5	6	7

• 第一次出栈

S:

0	1	2	3	4	5	6	7
1	3	4	5

Q:

0	1	2	3	4	5	6	7
2

• 第二次出栈（此时栈的元素最多为4）

S:

0	1	2	3	4	5	6	7
1	3	4	6

Q:

0	1	2	3	4	5	6	7
2	5

• 第三次出栈

S:

0	1	2	3	4	5	6	7
1	3	4

Q:

0	1	2	3	4	5	6	7
2	5	6

• 第四次出栈

S:

0	1	2	3	4	5	6	7
1	3	7

Q:

0	1	2	3	4	5	6	7
2	5	6	4

• 全部出栈

S:

0	1	2	3	4	5	6	7
1	3

Q:

0	1	2	3	4	5	6	7
2	5	6	4	7	3	1

13、若借助堆栈将中缀表达式a+b*c+(d*e+f)*g转换为后缀表达式，当读入f时，堆栈里的内容是什么（按堆栈自底向上顺序）？ (B)

1. +(*+
2. +(+
3. ++(+
4. abcde

解析：
步骤

• 当输入的是操作数时，直接输出a;
• 遇到操作符，如果栈为空入栈，+入栈

0	1	2	3
+

• 当输入的是操作数时，直接输出b;
• 当输入的是运算符，栈顶运算符的优先级不低于输入的运算符的优先级，将栈顶元素弹出，把输入的运算符op 压栈；栈顶元素+的优先级小于*的优先级，* 压栈;

0	1	2	3
+	*

• 当输入的是操作数时，直接输出c;
• 当输入的是运算符，栈顶元素*的优先级大于+的优先级，* 出栈;循环，栈顶元素+的优先级等于+的优先级，+ 出栈，+入栈；

0	1	2	3
+

• 当输入的是开括号时，把它压栈;

0	1	2	3
+	(

• 当输入的是操作数时，直接输出d;
• 当输入的是运算符，因为栈顶是开括号，* 压栈；

0	1	2	3
+	(	*

• 当输入的是操作数时，直接输出e;
• 当输入的是运算符，栈顶元素*的优先级大于+的优先级，* 出栈;+入栈；

0	1	2	3
+	(	+

• 当输入的是f停止，此时栈中+(+;

14、在一个不带头结点的非空链式队列中,假设f和r分别为队头和队尾指针,则插入s所指的结点运算是( B)。

1. f->next=s; f=s;
2. r->next=s; r=s;
3. s->next=s; r=s;
4. s->next=f; f=s;

15、假设有5个整数以1、2、3、4、5的顺序被压入堆栈，且出栈顺序为3、5、4、2、1，那么为了获得这样的输出，堆栈大小至少为： (C )

1. 2
2. 3
3. 4
4. 5

解析：

0	1	2	3	4
1	2	3

• 第一次出栈3：（栈元素最多为4）

0	1	2	3	4
1	2	4	5

• 全部出栈，出栈5，4，2，1：

16、设栈S和队列Q的初始状态均为空，元素a、b、c、d、e、f、g依次进入栈S。若每个元素出栈后立即进入队列Q，且7个元素出队的顺序是b、d、c、f、e、a、g，则栈S的容量至少是： (C )

1. 1
2. 2
3. 3
4. 4

解析：
S:

0	1	2	3	4	5	6	7
a	b

Q:

0	1	2	3	4	5	6	7

• 第一次出栈

S:

0	1	2	3	4	5	6	7
a	c	d

Q:

0	1	2	3	4	5	6	7
b

• 第二次出栈（此时栈的元素最多为3）

S:

0	1	2	3	4	5	6	7
a	e	f

Q:

0	1	2	3	4	5	6	7
b	d	c

• 第三次出栈

S:

0	1	2	3	4	5	6	7
g

Q:

0	1	2	3	4	5	6	7
b	d	c	f	e	a

• 全部出栈

S:

0	1	2	3	4	5	6	7

Q:

0	1	2	3	4	5	6	7
b	d	c	f	e	a	g

17、用单链表表示的链队的队头在链表的（A）位置。

1. 链头
2. 链尾
3. 链中
4. 均可以

18、设一个栈的输入序列是 1、2、3、4、5，则下列序列中，是栈的合法输出序列的是？（A）

1. 3 2 1 5 4

2. 5 1 2 3 4

3. 4 5 1 3 2

4. 4 3 1 2 5

解析：
2一定在1的后面；

19、栈和队列的共同点(C )。

1. 都是先进先出
2. 都是后进先出
3. 只允许在端点处插入和删除元素
4. 没有共同点

三、填空题

1、栈的运算遵循 (先进后出)的原则。

2、为了解决队列的假溢出现象，应采用 (循环)队列。

3、The value of reverse Polish notation(逆波兰式) (also known as postfix expression) $12345-+/\ast$is (1) 。（如计算结果不是整数，则保留一位小数）
翻译：
后缀表达式的$12345-+/\ast$的值为：（）
解析：
1*(2/(3+(4-5)))=1;

4、(队列)又称为先进先出的线性表。

5、下面程序的输出结果是 (1 2 1 3 1 2 1 4 1 2 1 3 1 2 1)。注意：每个数据后有一个空格。

#include 
void fun(int n)
{
 	if(n > 0)
 	{
 		fun(n-1);
		printf("%d ", n);
		fun(n-1);
	}
}
int main()
{
	fun(4);
 	return 0;
}

6、The value of reverse Polish notation(逆波兰式) (also known as postfix expression) 1 2 3 4 - / * 5 + is (3) 。（如计算结果不是整数，则保留一位小数。）
解析：

• 3-4=-1
• 2/-1=-2
• 1*-2=-2
• -2+5=3

四、程序填空

1、本题要求求出不带头结点的单链表中的最大值并返回。

/* 求单链表值最大的结点 */
int getMaxNode(LinkNode* head)
{
	if (head == NULL)
		return INT_MIN;
	int first = head->data;
	int m = getMaxNode(head->next);//填空
	if (m > first)return m;
	else return first;
}

2、本题要求采用递归方式求不带头结点的单链表的长度。
其中, 单链表结点类型定义如下:

typedef struct LNode {
	int data;
	struct LNode* next;
} LinkNode;
///求单链表长度
int getLength(LinkNode* L) {
	if (L == NULL)
		return 0;
	return getLength(L->next)+1;//填空
}

五、函数题

1、带头结点的链队列的基本操作

实现链队列的入队列及出队列操作。

函数接口定义：

Status QueueInsert(LinkQueue *Q,ElemType e)；

Status QueueDelete(LinkQueue *Q,ElemType *e)；

其中 Q 和 e 都是用户传入的参数。 LinkQueue 的类型定义如下：

typedef int ElemType; 
typedef struct LNode
{
    ElemType data;
	struct LNode * next;
}LNode,*LinkList;
typedef struct
 {
   LinkList front,rear; /* 队头、队尾指针 */
 }LinkQueue;

裁判测试程序样例：

#include 
#include
#define OK 1
#define ERROR 0
typedef int Status;
typedef int ElemType; 
typedef struct LNode
{
    ElemType data;
	struct LNode * next;
}LNode,*LinkList;

typedef struct
 {
   LinkList front,rear; /* 队头、队尾指针 */
 }LinkQueue;
 /* 带头结点的链队列的基本操作 */
 Status InitQueue(LinkQueue *Q)
 { /* 构造一个空队列Q */
	 LinkList p;
   p=(LNode*)malloc(sizeof(LNode)); 
   p->next=NULL;
   (*Q).rear=(*Q).front=p;
   return OK;
 }
Status List(LinkList L)
{
	LinkList p;
	if(!L) return ERROR;
	p=L->next;
	
	while(p)
	{
		printf(" %d",p->data);
		p=p->next;
	}
	printf("\n");
    return OK;
}

int QueueLenth(LinkQueue Q)
{
	int n=0;
	LinkList p;
	if(Q.rear==Q.front)
		return 0;
	p=Q.front->next;
	while(p)
	{
		n++;
		p=p->next;
	}
	return n;
}

int main()
{
	int x;
	LinkQueue Q;
	InitQueue(&Q);
	QueueInsert(&Q,1);QueueInsert(&Q,2);QueueInsert(&Q,3);
	List(Q.front );
	QueueDelete( &Q,&x);
	printf(" %d %d\n",x,QueueLenth(Q));
	QueueDelete(&Q,&x);QueueDelete(&Q,&x);
	printf(" %d %d\n",x,QueueLenth(Q));
	return 0;
}

/* 请在这里填写答案 */

输出样例：

在这里给出相应的输出。例如：

 1 2 3
 1 2
 3 0

实现代码：

Status QueueInsert(LinkQueue *Q,ElemType e){
	LinkList rear;
	rear=(struct LNode*)malloc(sizeof(struct LNode));
	rear->data=e;
	rear->next=NULL;
	Q->rear->next=rear;
	Q->rear=rear;
}

Status QueueDelete(LinkQueue *Q,ElemType *e){
	if(Q->front==Q->rear)
	 return ERROR;
	*e=Q->front->next->data; 
	Q->front=Q->front->next;
	return OK;
}

2、另类堆栈
在栈的顺序存储实现中，另有一种方法是将 Top 定义为栈顶的上一个位置。请编写程序实现这种定义下堆栈的入栈、出栈操作。如何判断堆栈为空或者满？
函数接口定义：

bool Push( Stack S, ElementType X );
ElementType Pop( Stack S );

其中 Stack 结构定义如下：

typedef int Position;
typedef struct SNode *PtrToSNode;
struct SNode {
	ElementType *Data; /* 存储元素的数组 */
 	Position Top; /* 栈顶指针 */
	int MaxSize; /* 堆栈最大容量 */
};
typedef PtrToSNode Stack;

注意：如果堆栈已满，Push 函数必须输出“Stack Full”并且返回false；如果队列是空的，则 Pop 函数必须输出“Stack Empty”，并且返回 ERROR。
裁判测试程序样例：

#include 
#include 
#define ERROR -1
typedef int ElementType;
typedef enum { push, pop, end } Operation;
typedef enum { false, true } bool;
typedef int Position;
typedef struct SNode *PtrToSNode;
struct SNode {
	ElementType *Data; /* 存储元素的数组 */
	Position Top; /* 栈顶指针 */
 	int MaxSize; /* 堆栈最大容量 */
};
typedef PtrToSNode Stack;
Stack CreateStack( int MaxSize ) {
 	Stack S = (Stack)malloc(sizeof(struct SNode));
 	S->Data = (ElementType *)malloc(MaxSize * 											      
 	sizeof(ElementType));
 	S->Top = 0;
 	S->MaxSize = MaxSize;
 	return S;
}
bool Push( Stack S, ElementType X );
ElementType Pop( Stack S );
Operation GetOp(); /* 裁判实现，细节不表 */
void PrintStack( Stack S ); /* 裁判实现，细节不表 */
int main()
{
 	ElementType X;
 	Stack S;
 	int N, done = 0;
 	scanf("%d", &N);
 	S = CreateStack(N);
 	while ( !done ) {
 		switch( GetOp() ) {
 			case push:
 				scanf("%d", &X);
 				Push(S, X);
 				break;
 			case pop:
 				X = Pop(S);
 				if ( X!=ERROR ) printf("%d is out\n", X);
 				break;
 			case end:
 				PrintStack(S);
 				done = 1;
			 	break;
 		}
 	}
 	return 0;
}
/* 你的代码将被嵌在这里 */

输入样例：

4
Pop
Push 5
Push 4
Push 3
Pop
Pop
Push 2
Push 1
Push 0
Push 10
End

输出样例：

Stack Empty
3 is out
4 is out
Stack Full
0 1 2 5

实现代码：

bool Push( Stack S, ElementType X ){
    if(S->Top==S->MaxSize){
        printf("Stack Full\n");
        return false;
    }
    else{
        S->Data[S->Top++] = X;
        return true;
    }
}
ElementType Pop( Stack S ){
    if(S->Top==0){
        printf("Stack Empty\n");
        return ERROR;
    }
    else{
        return ( S->Data[--S->Top] );
    }
}

下一节：算法与数据结构复习 第四章 字符串