数字图像处理(四)——Matlab实现图像几何变换
实验内容
已知3×3的图像如图所示:
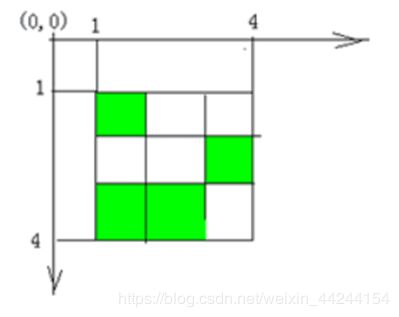
A、将此图以图形中心为轴顺时针旋转30度。
B、将此图放大二倍。
C、对此图作水平镜像。
D、对此图作垂直方向的错切。
1.1使用matlab制作出题目所要求的图形。
定义一个a=zeros(300,300,3)的三维矩阵,用for循环对该矩阵中的每个像素点进行赋值运算,给出不同的值作为该图像每个像素点的灰度级,生成的图像如图所示:

1.2将此图以图形中心为轴顺时针旋转30度。
首先定义旋转角度为pi/6,即三十度,其次算出旋转后图像的矩阵大小,得到旋转后图像的长和宽,然后利用两个for循环遍历旋转后图像中的每个像素点,先将旋转中心移至原点,然后利用逆矩阵得到旋转后图像的坐标x和y在原图像中的坐标点x0、y0,由于在原图像中的坐标可能出现小数,因此利用最邻近插值算法对x0、y0进行四舍五入取整运算,然后再将旋转中心移至左上角,得到旋转后的图像如图所示:

过观察可发现旋转后的图像在边界处出现了不同程度的凹凸不平的噪声点,这是由于在处理旋转后图像坐标映射到原图坐标时太过于粗糙所导致的,此时采用双线性插值算法,让处理更为精细,处理后的图像如图所示:

1.3将此图放大二倍。
图像放大与图像旋转类似,都是遍历变换后的图像每个像素点,然后在原图中找出对应的像素点坐标,同样用最邻近插值放大后的图像如图所示:

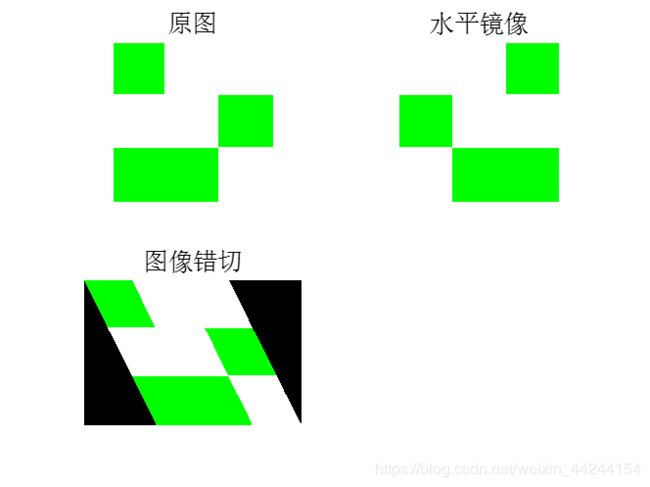
1.4对此图作水平镜像与垂直方向的错切
水平镜像即将y方向的坐标作对称变换即可,垂直方向的错切则是对y方向的坐标点进行变换,变换后的图像如图所示:
实验代码附录如下:
clc
close all
a=zeros(300,300,3);
%%
%生成图像
for i=1:100
for j=1:100
a(i,j,2)=50;
a(i,j,1)=0;
a(i,j,3)=0;
end
end
for i=100:200
for j=200:300
a(i,j,2)=50;
a(i,j,1)=0;
a(i,j,3)=0;
end
end
for i=200:300
for j=1:200
a(i,j,2)=50;
a(i,j,1)=0;
a(i,j,3)=0;
end
end
for i=1:100
for j=100:300
a(i,j,1)=255;
a(i,j,2)=255;
a(i,j,3)=255;
end
end
for i=100:200
for j=1:200
a(i,j,1)=255;
a(i,j,2)=255;
a(i,j,3)=255;
end
end
for i=200:300
for j=200:300
a(i,j,1)=255;
a(i,j,2)=255;
a(i,j,3)=255;
end
end
figure;
imshow(a);
%%
%图像旋转
row=300;
col=300;
dushu= pi/6; %旋转角度
row1 = round(abs(row*cos(dushu)) + abs(col*sin(dushu))); %旋转后大小
col1 = round(abs(col*cos(dushu)) + abs(row*sin(dushu)));
I1 = zeros(row1, col1,3);
for i = 1:row1
for j = 1:col1
c = i - row1/2; %将旋转中心移至原点
d = j - col1/2;
x = c*cos(dushu) - d*sin(dushu); %旋转
y = d*cos(dushu) + c*sin(dushu);
x = round(x + row/2); %将所需图像移至坐标系正值部分
y = round(y + col/2);
if x > 0 && x <= row && y <= col && y > 0
I1(i,j,1) = a(x,y,1);
I1(i,j,2) = a(x,y,2);
I1(i,j,3) = a(x,y,3);
end
end
end
figure;
imshow(I1);
%%
%使用双线性插值处理
row=300;
col=300;
dushu= pi/6; %旋转角度
row1 = round(abs(row*cos(dushu)) + abs(col*sin(dushu))); %旋转后大小
col1 = round(abs(col*cos(dushu)) + abs(row*sin(dushu)));
I2 = zeros(row1, col1,3);
for i = 1:row1
for j = 1:col1
c = i - row1/2; %将旋转中心移至原点
d = j - col1/2;
x = c*cos(dushu) - d*sin(dushu); %旋转
y = d*cos(dushu) + c*sin(dushu);
x = x + row/2; %将所需图像移至坐标系正值部分
y = y + col/2;
if x > 0 && x <= row && y <= col && y > 0
if x < 1 %边界处理
x = 1;
end
if y < 1
y = 1;
end
p=x-floor(x);
q=y-floor(y);
I2(i,j,1)=(1-q)*(1-p)*a(floor(x),floor(y),1)+(1-q)*p*a(ceil(x),floor(y),1)+q*(1-p)*a(floor(x),ceil(y),1)+q*p*a(ceil(x),ceil(y),1);
I2(i,j,2)=(1-q)*(1-p)*a(floor(x),floor(y),2)+(1-q)*p*a(ceil(x),floor(y),2)+q*(1-p)*a(floor(x),ceil(y),2)+q*p*a(ceil(x),ceil(y),2);
I2(i,j,3)=(1-q)*(1-p)*a(floor(x),floor(y),3)+(1-q)*p*a(ceil(x),floor(y),3)+q*(1-p)*a(floor(x),ceil(y),3)+q*p*a(ceil(x),ceil(y),3);
end
end
end
figure;
imshow(I2);
%%
%图像水平镜像
b=a;
for i=1:300
for j=1:300
x1=i;
y1=300-j+1;
b(x1,y1,1)=a(i,j,1);
b(x1,y1,2)=a(i,j,2);
b(x1,y1,3)=a(i,j,3);
end
end
%%
%图像放大两倍
%最邻近插值
c=a;
row1=2*row;
col1=2*col;
for i=1:600
for j=1:600
x=round(i/2);
y=round(j/2);
c(i,j,1)=a(x,y,1);
c(i,j,2)=a(x,y,2);
c(i,j,3)=a(x,y,3);
end
end
figure;
imshow(c);
%%
%双线性插值
c1=a;
for i=1:600
for j=1:600
x=i/2;
y=j/2;
if x < 1 %边界处理
x = 1;
end
if y < 1
y = 1;
end
p=x-floor(x);
q=y-floor(y);
c1(i,j,1)=(1-q)*(1-p)*a(floor(x),floor(y),1)+(1-q)*p*a(ceil(x),floor(y),1)+q*(1-p)*a(floor(x),ceil(y),1)+q*p*a(ceil(x),ceil(y),1);
c1(i,j,2)=(1-q)*(1-p)*a(floor(x),floor(y),2)+(1-q)*p*a(ceil(x),floor(y),2)+q*(1-p)*a(floor(x),ceil(y),2)+q*p*a(ceil(x),ceil(y),2);
c1(i,j,3)=(1-q)*(1-p)*a(floor(x),floor(y),3)+(1-q)*p*a(ceil(x),floor(y),3)+q*(1-p)*a(floor(x),ceil(y),3)+q*p*a(ceil(x),ceil(y),3);
end
end
figure;
imshow(c1);
%%
%图像错切
d=zeros(300,300,3);
dx=0.5;
for i=1:300
for j=1:300
x=i;
y=round(j+dx*i);
d(x,y,1)=a(i,j,1);
d(x,y,2)=a(i,j,2);
d(x,y,3)=a(i,j,3);
end
end
figure;
subplot(2,2,1),imshow(a),title('原图','fontsize',16);
subplot(2,2,2),imshow(b),title('水平镜像','fontsize',16);
subplot(2,2,3),imshow(d),title('图像错切','fontsize',16);
