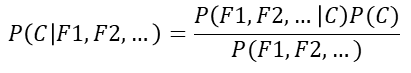朴素贝叶斯算法
1. 概念
朴素贝叶斯算法(Naive Bayesian algorithm)是基于贝叶斯定理与特征条件独立假设的分类方法, 朴素贝叶斯模型发源于古典数学理论,是应用最为广泛的分类算法之一。
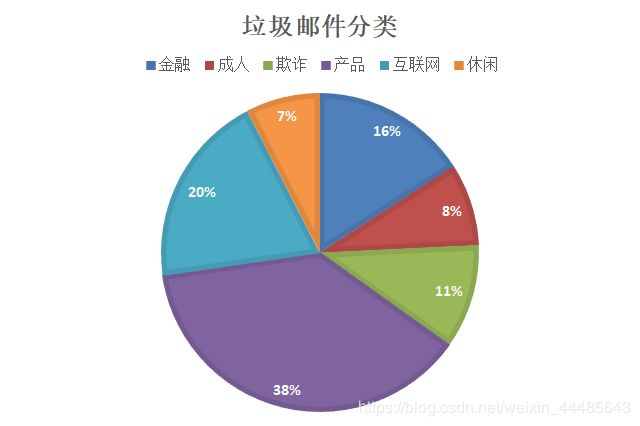
如上图,在收到的中,判断出邮件为产品的概率最大为38%,于是可以将这封邮件判断为垃圾邮件
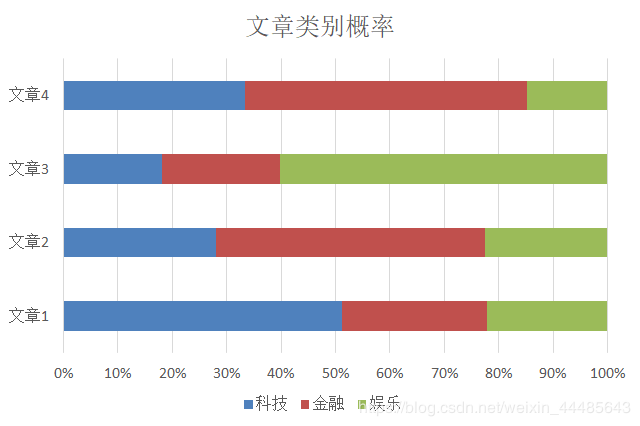
如上图,文章1 为科技类的可最大,文章2为金融的概率最大等,这都是有朴素贝叶斯实现的。
2. 概率基础
谈到朴素贝叶斯就不得不谈到概率统计。
1) 联合概率,条件概率,相互独立
- 联合概率:包含多个条件,且所有条件同时成立的概率 P(A,B)。
- 条件概率:事件A在事件B已经发生条件下发生的概率 P(A|B)。
- 相互独立:P(A,B) = P(A)*P(B) 则事件A与事件B相互独立。
我们结合案例来详细说明以上概念:
Example:
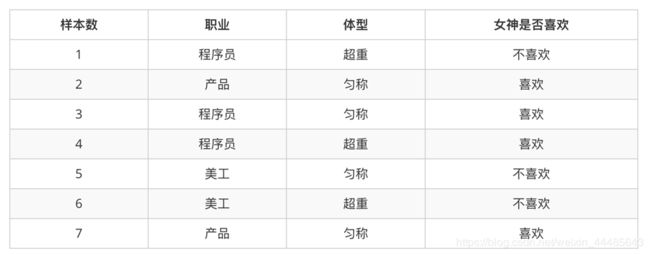
<1> 女神喜欢的概率:
共有样本7个其中喜欢有4个,故女神喜欢的概率为:
P(喜欢) = 4/7
<2> 职业是程序员并且体型匀称的概率:
P(程序员,匀称) = 1/7,这是典型的联合概率
<3> 女神喜欢的条件下,职业是程序员的概率:
因为是在喜欢的条件下,所以样本的数量发生变化,不在是7个,而是4个。
故在当前样本下,职业是程序员的概率为:
P(程序员|喜欢) = 2/4 = 1/2 ,这是典型的条件概率
- problem
回顾问题二,
P(程序员,匀称) = 1/7 ,
P(程序员)*P(匀称) = 3/7 *4/7 = 12/49 ,
很明显 这两者不想等,根据相互独立的概念,这能说明职业和体型有关系吗?
结果是否定的,职业和体型并没有什么关系,之所以出现这样的结果,是因为我们的样本量很少,这也侧面反映了数据量的多少对结果的影响程度。
3. 贝叶斯与朴素贝叶斯
如上例,若小明职业是产品,体型超重,那么他是否会被女神喜欢呢?
这是一个典型的 多个条件下求一个结果的概率问题,并不符合条件概率一个条件下,多个结果的概率
要预测这个问题,就必须引入贝叶斯公式:
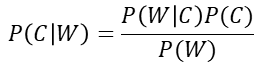
注: W为给定文档的特征值,C为文档类别
公式分为三个部分:
- P( C):某个文档类别的概率。(某文档类别数 / 总文档数)
- P(F1|C):给定类别下特征(被预测文档中出现的词)的概率。
P(F1|C) = Ni / N,P(F1|C) = Ni+α / N+αm 引入拉普拉斯平滑系数,后面会介绍。
Ni 为该词F1在C类别所有文档中出现的次数。
N 为所属文档类别C下的文案中所有词出现的次数和。
α : 拉普拉斯平滑系数,一般取1.0。
m : 训练文档中统计出的特征词个数。 - P(F1,F2,…) 预测文档中每个词的概率。
运用贝叶斯
故:P(喜欢|产品,超重) = [P(产品,超重|喜欢)P(喜欢)] / P(产品,超重)
分子:
P(产品,超重|喜欢) = 0 ,P(喜欢) = 4/7
分母:
P(产品,超重) = 0
很明显这里存在很大的问题:
P(产品,超重|喜欢) = 0 和 P(产品,超重) = 0
难道职业是产品经历,体型超重的人就不配拥有爱情?
答案是否定的,还是因为样本太少导致的结果
此时,贝叶斯公式就解决不了问题
运用朴素贝叶斯
1)朴素:
假设特征与特征之间是相互独立
2)朴素贝叶斯:
朴素 + 贝叶斯
在朴素的条件下:
P(产品,超重) = P(产品)*P(超重) = 2/7 * 3/7 = 6/49
P(产品,超重|喜欢) = P(产品|喜欢)*P(超重|喜欢) = 1/2 * 1/4 = 1/8
故可求出:
P(喜欢|产品,超重) = [P(产品,超重|喜欢)*P(喜欢)] / P(产品,超重) = (1/8 * 4/7) / (6/49)= 7/12
职业是产品,体型超重 被女神喜欢的概率为 7/12 那么这个结果符合实际吗?→_→
答案是否定的,7/12都超过一半的可能了,造成这么不准确的原因一方面是因为样本数不足,另一方面我们假设了特征之间相互独立,所以结果不准确。
在现实使用中,我们的样本量将会是非常巨大的,这样结果就会相对准确。
4. 应用场景
- 文本分类
- 情感分析
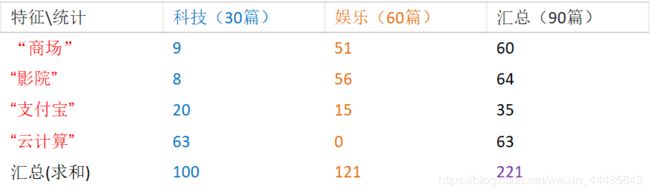
5. 文章分类统计
模型解读:如科技类型文章中,“商场” 出现9次,“影院”出现8次,“支付宝”出现20次,“云计算”出现63次。
现有一篇文章出现了影院,支付宝,云计算等词,计算其属于科技和娱乐类别的概率?
使用朴素贝叶斯,则其概率分别为:
P(科技|影院,支付宝,云计算)
两个概率分母相同,故在这里可不管。
= P(影院,支付宝,云计算|科技) * P(科技)/ P(影院,支付宝,云计算)
= P(影院|科技) * P(支付宝|科技) * P(云计算|科技) * P(科技)
= (8/100) * (20/100) * (63/100) * (30/90)
= 0.00456109
P(娱乐|影院,支付宝,云计算)
= P(影院,支付宝,云计算|娱乐) * P(娱乐)/ P(影院,支付宝,云计算)
= P(影院|娱乐) * P(支付宝|娱乐) * P(云计算|娱乐) * P(娱乐)
= (56/121) * (15/121) *(0/121)* (60/90)
= 0
在这里我们先不考虑 P(娱乐|影院,支付宝,云计算) 概率为0是否合理,根据计算结果,属于科技的概率大于属于娱乐的概率,应该将这篇文章分类为科技类型。这就是朴素贝叶斯对文章进行分类的原理。
- problem
在预测过程中,预测出为某个类别的概率为0合适吗?
答案是否定的,如上例中,计算结果为0的原因是在我们给定的训练模型中,娱乐文章中 “云计算” 这个词出现了0次,才导致的。
所以说这个训练好的模型并不是很完善,模型的好坏直接影响了预测结果的合理与准确性。
而拿去训练的数据集的质量与数量又影响者模型好坏,给定的模型中,仅仅使用了90篇文章去训练,这是远远不够的,若没有个几万~几千万的样本去训练模型,最终预测准确的概率不会令人满意,所以,至此出现的所有问题都是因为数据集,样本的数量不足,由此看出,机器学习对海量数据与计算量的依赖,这也是为什么,从1980年机器学习称为一个独立的方向开始算起,到现在也已经过去了近40年,才繁荣起来。
- solution
上述问题的解决办法一般有两种:
- 既然样本不足,那就收集足够的样本后去训练出更好的模型。
ps:废话 - 在计算中引入 拉普拉斯平滑系数。
背景:为什么要做平滑处理?
零概率问题,就是在计算实例的概率时,如果某个量x,在观察样本库(训练集)中没有出现过,会导致整个实例的概率结果是0。在文本分类的问题中,当一个词语没有在训练样本中出现,该词语调概率为0,使用连乘计算文本出现概率时也为0。这是不合理的,不能因为一个事件没有观察到就武断的认为该事件的概率是0。
拉普拉斯的理论支撑
为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑。
假定训练样本很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。
引入拉普拉斯后的朴素贝叶斯,则其概率分别为:
P(科技|影院,支付宝,云计算)
= P(影院,支付宝,云计算|科技) * P(科技)/ P(影院,支付宝,云计算)
= P(影院|科技) * P(支付宝|科技) * P(云计算|科技) * P(科技)
= (8+1/100+14) * (20+1/100+14) * (63+1/100+14) * (30+1/90+14)
≠0
P(娱乐|影院,支付宝,云计算)
= P(影院,支付宝,云计算|娱乐) * P(娱乐)/ P(影院,支付宝,云计算)
= P(影院|娱乐) * P(支付宝|娱乐) * P(云计算|娱乐) * P(娱乐)
= (56+1/121+14) * (15+1/121+14) * (0+1/121+1*4) * (60/90)
≠0
经过拉普拉斯平滑处理后,就不会出现概率为0 的问题了。注意的是不能只对原来概率为0的进行平滑处理,而是对所有的概率都进行处理。
6. 总结
- 优点:
1. 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2. 对缺少数据不太敏感(一篇文章中缺少几个词不会影响其分类),算法比较简单,常用于文本分析。
3. 分类准确度高,速度块。 - 缺点:
由于假定特征之间相互独立,所以如果特征属性有关联时,效果不好。
比如:我爱北京天安门。
在这个文本中‘北京’ 和 ‘天安门’是有关联的。如果使用朴素贝叶斯去进行分类,效果还 是不太好。