信息论与编码-python实现三种编码(香农编码,费诺编码,赫夫曼编码)

香农编码，费诺编码，赫夫曼编码（python实现）

开始参考了网上其他人的代码，但后来都发现要么代码有错误，要么输出结果不符合自己的预期，于是就重新实现了一下，代码仍存在一些小问题，但是能够满足作业要求，重要的是看懂思路，然后按照自己的想法去实现

代码存在的问题：

1. 香农编码和费诺编码起始的符号及其概率都已给出并且做了初步处理，有想法的可以改成用户自定义输入
2. 费诺编码的实现借助了字典和递归，但是如果初始输入的概率集中存在相同的key(也就是概率集中存在相同概率)，那么字典update()方法的覆盖特性会使两个相同概率对应的码字合并(因为事情比较多，就没有改代码，有带佬知道怎么解决的话求帮助)
3. 赫夫曼编码借鉴了别人的代码，初始数据是用户自定义输入的

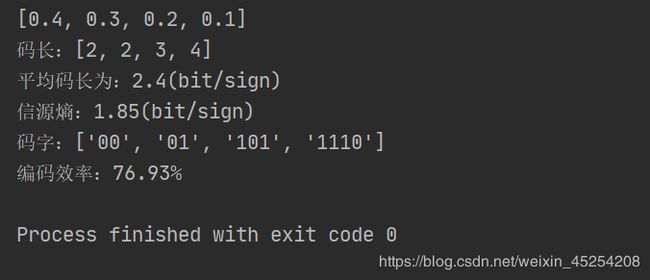
香农编码

Code:

import math

p = [0.4, 0.3, 0.2, 0.1]        # 信源符号概率递减排列
p_next = [0, 0.4, 0.7, 0.9]     # 概率累加和
k = []          # 对应码长
length_k = 0    # 平均码长
H = 0           # 信源熵

def code_length():
    for i in range(len(p)):
        k.append(int(math.log(p[i], 2) * (-1) + 0.99))
    print('码长：{}'.format(k))

def average_length():
    global  length_k
    for i in range(len(p)):
        length_k += k[i] * p[i]
    # print(round(length_k, 1))
    print("平均码长为：{:.3}(bit/sign)".format(length_k))


# 将十进制小数转为二进制小数
def int_to_bin(px):
    b = []
    while True:
        px *= 2
        b.append(1 if px>=1 else 0)
        px -= int(px)
        if px == 0:
            for i in range(len(p)):
                if len(b) != k[i]:
                    b.append('0'*(k[i]-len(b)))
            break
    return b

def codeword():
    code = []  # 对应码字
    for i in range(len(p)):
        e = ''
        for j in range(k[i]):
            e += str(int_to_bin(p_next[i])[j])
        code.append(e)
    print('码字：{}'.format(code))

def Hx():
    global H
    for i in range(len(p)):
        H += p[i] * math.log(p[i], 2) * (-1)
    # print(round(H, 2))
    print('信源熵：{:.3}(bit/sign)'.format(H))

def efficiency():
    print('编码效率：{:.2%}'.format(H/length_k))

if __name__ == '__main__':
    print(p)
    code_length()       # 求对应码长
    average_length()    # 求平均码长
    Hx()                # 求信源熵
    codeword()          # 求码字
    efficiency()        # 求编码效率

Result:

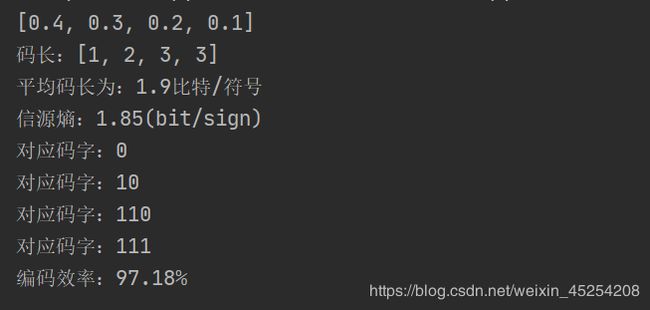
费诺编码

Code:

import math

p = [0.4, 0.3, 0.2, 0.1]      # 信源符号概率递减排列
k = []          # 码长
length_k = 0    # 平均码长
code = {}       # 符号及其对应的码字集合
list_code = []
H = 0           # 信源熵
# 编码空间
encode_dictionary = {}

def code_length():
    for p in list_code:
        k.append(len(code[p]))
    print('码长：{}'.format(k))

def average_length():
    global length_k

    for p in list_code:
        length_k += len(code[p]) * p
    print("平均码长为：{:.3}比特/符号".format(length_k))

def codeword(px, encode_dictionary):
    if len(px) == 1:
        return 1

    # 最佳分组位置
    flag = 1
    find_position = 1

    for i in range(len(px)):
        sum1 = 0
        sum2 = 0
        for j in range(i+1):
            sum1 += px[i]
        for j in range(i+1,len(px)):
            sum2 += px[j]
        difference = abs(sum1 - sum2)
        if difference < flag:
            flag = difference
            find_position = i+1

    # 编码
    for i in range(len(px)):
        if i < find_position:
            element = {px[i] : encode_dictionary[px[i]] + '0'}
            encode_dictionary.update(element)
        else:
            element = {px[i] : encode_dictionary[px[i]] + '1'}
            encode_dictionary.update(element)

    # 编码分组
    leftgroup = []
    rightgroup = []
    for i in range(find_position):
        leftgroup.append(px[i])
    for i in range(find_position, len(px)):
        rightgroup.append((px[i]))

    # 递归编码
    codeword(leftgroup, encode_dictionary)
    codeword(rightgroup, encode_dictionary)
    # 返回编码空间
    return encode_dictionary

def Hx():
    global H
    for i in range(len(p)):
        H += p[i] * math.log(p[i], 2) * (-1)
    # print(round(H, 2))
    print('信源熵：{:.3}(bit/sign)'.format(H))


def efficiency():
    print('编码效率：{:.2%}'.format(H/length_k))

if __name__ == '__main__':
    # 初始化编码空间
    for i in range(len(p)):
        element = {p[i]: ""}
        encode_dictionary.update(element)

    print(p)

    # 求码字
    code = codeword(p, encode_dictionary)
    list_code = list(code)
    code_length()  # 求码长
    average_length()  # 平均码长
    Hx()  # 求信源熵
    for p in list_code:
        print('对应码字：{}'.format(code[p]))

    efficiency()        # 求编码效率

Result:

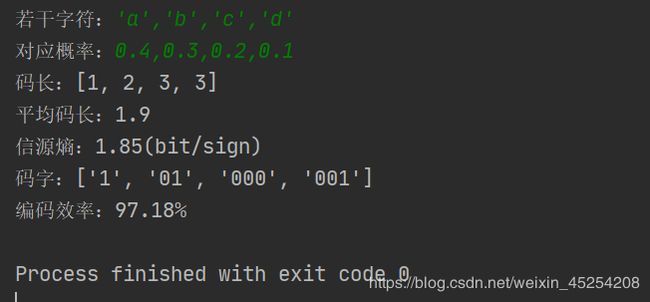
赫夫曼编码

Code:

import math

# 码长
def code_length():
    list_code = list(code)
    for i in range(len(list_code)):
        k.append(len(code[s[i]]))
    print('码长：{}'.format(k))

def Hx():
    global H
    for i in range(len(s)):
        H += w[i] * math.log(w[i], 2) * (-1)
    # print(round(H, 2))
    print('信源熵：{:.3}(bit/sign)'.format(H))

# 平均码长
def huffmanCode(root, tree, rootCode='', codeDict={}, depth=1, res=0):
    # 对左子树进行处理：如果是叶子节点，就打印编码；否则递归
    if len(root['left'][0]) == 1:
        codeDict[root['left'][0]] = '0' + rootCode
        res += (len(rootCode) + 1) * root['left'][1]  # 计算平均位数
    else:
        codeDict, res = huffmanCode(tree[root['left'][0]], tree, '0' + rootCode, codeDict, depth + 1, res)

    # 对右子树进行处理：如果是叶子节点，就打印编码；否则递归
    if len(root['right'][0]) == 1:
        codeDict[root['right'][0]] = '1' + rootCode
        res += (len(rootCode) + 1) * root['right'][1]  # 计算平均位数
    else:
        codeDict, res = huffmanCode(tree[root['right'][0]], tree, '1' + rootCode, codeDict, depth + 1, res)

    return codeDict, res


s = eval(input('若干字符：'))
w = eval(input('对应概率：'))

# 合并成一个字典
arr = [[s[i], w[i]] for i in range(len(s))]

tree = {}
while len(arr) > 1:
    # 1 根据权重排序
    arr.sort(key=lambda x: x[1])

    # 2 选出最小的两个节点，分别作为左子树，右子树
    l = arr[0]  # 较小的作为左子树
    r = arr[1]  # 较大者作为右子树

    if len(arr) > 2:
        tree[l[0] + r[0]] = {'left': l, 'right': r}

        # 3 用新节点置换这两个节点
        arr = arr[2:]
        arr.append([l[0] + r[0], l[1] + r[1]])
    else:
        tree['root'] = {'left': l, 'right': r}
        break

code, res = huffmanCode(tree['root'], tree)
# 码长k
k = []
H = 0
code_length()
print('平均码长：{:.3}'.format(res/sum(w)))
Hx()
# 码字m
m = []
for i in range(len(s)):
    x = str(code[s[i]].replace('1','2'))
    y = x.replace('0','1')
    z = y.replace('2','0')
    n = list(z)
    n.reverse()
    m.append(''.join(n))
print('码字：{}'.format(m))
print('编码效率：{:.2%}'.format(H / round(res/sum(w),3)))

# 'a','b','c','d'
# 0.4,0.3,0.2,0.1

Result:

总结

由上可得，相同的数据，使用不同的编码，效率也不相同
编码效率：赫夫曼编码 >= 费诺编码 > 香农编码

上面费诺编码和赫夫曼编码的编码效率不都是97.18%吗？
为什么赫夫曼编码的编码效率不是应该等于费诺编码的编码效率吗？
我觉得这个应该是特殊情况