无监督学习 | PCA 主成分分析之客户分类

相关文章：

机器学习 | 目录

机器学习 | 聚类评估指标

无监督学习 | KMeans 之Sklearn实现：电影评分聚类

无监督学习 | PCA 主成分分析原理及Sklearn实现

1. 开始

在这个项目中，我们将分析一个数据集的内在结构，这个数据集包含很多客户真对不同类型产品的年度采购额（用金额表示）。这个项目的任务之一是如何最好地描述一个批发商不同种类顾客之间的差异。这样做将能够使得批发商能够更好的组织他们的物流服务以满足每个客户的需求。

这个项目的数据集能够在UCI机器学习信息库中找到.因为这个项目的目的，分析将不会包括 ‘Channel’ 和 ‘Region’ 这两个特征——重点集中在6个记录的客户购买的产品类别上。

# 引入这个项目需要的库
import numpy as np
import pandas as pd
import visuals as vs   # 子集
from IPython.display import display # 使得我们可以对DataFrame使用display()函数

# 设置以内联的形式显示matplotlib绘制的图片（在notebook中显示更美观）
%matplotlib inline
# 高分辨率显示
%config InlineBackend.figure_format='retina'

# 载入整个客户数据集
try:
    data = pd.read_csv("customers.csv")
    data.drop(['Region', 'Channel'], axis = 1, inplace = True)
    print("Wholesale customers dataset has {} samples with {} features each.".format(*data.shape))
except:
    print("Dataset could not be loaded. Is the dataset missing?")

Wholesale customers dataset has 440 samples with 6 features each.

data.head()

	Fresh	Milk	Grocery	Frozen	Detergents_Paper	Delicatessen
0	12669	9656	7561	214	2674	1338
1	7057	9810	9568	1762	3293	1776
2	6353	8808	7684	2405	3516	7844
3	13265	1196	4221	6404	507	1788
4	22615	5410	7198	3915	1777	5185

2. 数据探索

在这部分，我们将开始分析数据，通过可视化和代码来理解每一个特征和其他特征的联系。我们会看到关于数据集的统计描述，考虑每一个属性的相关性，然后从数据集中选择若干个样本数据点，我们将在整个项目中一直跟踪研究这几个数据点。

运行下面的代码单元给出数据集的一个统计描述。注意这个数据集包含了6个重要的产品类型：‘Fresh’, ‘Milk’, ‘Grocery’, ‘Frozen’, **‘Detergents_Paper’**和 ‘Delicatessen’。想一下这里每一个类型代表你会购买什么样的产品。

# 显示数据集的一个描述
display(data.describe())

	Fresh	Milk	Grocery	Frozen	Detergents_Paper	Delicatessen
count	440.000000	440.000000	440.000000	440.000000	440.000000	440.000000
mean	12000.297727	5796.265909	7951.277273	3071.931818	2881.493182	1524.870455
std	12647.328865	7380.377175	9503.162829	4854.673333	4767.854448	2820.105937
min	3.000000	55.000000	3.000000	25.000000	3.000000	3.000000
25%	3127.750000	1533.000000	2153.000000	742.250000	256.750000	408.250000
50%	8504.000000	3627.000000	4755.500000	1526.000000	816.500000	965.500000
75%	16933.750000	7190.250000	10655.750000	3554.250000	3922.000000	1820.250000
max	112151.000000	73498.000000	92780.000000	60869.000000	40827.000000	47943.000000

2.2 特征相关性

一个有趣的想法是，考虑这六个类别中的一个（或者多个）产品类别，是否对于理解客户的购买行为具有实际的相关性。也就是说，当用户购买了一定数量的某一类产品，我们是否能够确定他们必然会成比例地购买另一种类的产品。

有一个简单的方法可以检测相关性：我们用移除了某一个特征之后的数据集来构建一个监督学习（回归）模型，然后用这个模型去预测那个被移除的特征，再对这个预测结果进行评分，看看预测结果如何。

在下面的代码单元中将实现以下的功能：

• 使用 DataFrame.drop 函数移除数据集中选择的不需要的特征，并将移除后的结果赋值给 new_data 。

• 使用 sklearn.model_selection.train_test_split 将数据集分割成训练集和测试集。

• 导入一个 DecisionTreeRegressor （决策树回归器），然后用训练集训练它。

• 使用回归器的 score 函数输出模型在测试集上的预测得分。

# 为DataFrame创建一个副本，用'drop'函数丢弃特征‘Milk’
new_data = data.drop('Milk',axis=1)

# 使用给定的特征作为目标，将数据分割成训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(new_data, data['Milk'],test_size=0.25,random_state=20)

# 创建一个DecisionTreeRegressor（决策树回归器）并在训练集上训练它
from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(random_state=20)
regressor.fit(X_train,y_train)

# 输出在测试集上的预测得分
from sklearn.metrics import r2_score
score = r2_score(regressor.predict(X_test),y_test)
score

0.6051738800058682

可以看到决定系数为 0.6052，并不是很高，因此这个特征对与区分用户的消费习惯来说不是特别的重要。

2.3 可视化特征分布

为了能够对这个数据集有一个更好的理解，我们可以对数据集中的每一个产品特征构建一个散布矩阵（scatter matrix）。如果在一个特征对于区分一个特定的用户来说是必须的，那么这个特征和其它的特征可能不会在下面的散射矩阵中显示任何关系。相反的，如果这个特征对于识别一个特定的客户是没有作用的，那么通过散布矩阵可以看出在这个数据特征和其它特征中有关联性。下面创建一个散布矩阵。

# 对于数据中的每一对特征构造一个散布矩阵
pd.plotting.scatter_matrix(data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');

由散步矩阵的对角图像可以看出，数据并不是正态，而是右偏的。

再看看相关系数矩阵以及热力图：

data.corr()

	Fresh	Milk	Grocery	Frozen	Detergents_Paper	Delicatessen
Fresh	1.000000	0.100510	-0.011854	0.345881	-0.101953	0.244690
Milk	0.100510	1.000000	0.728335	0.123994	0.661816	0.406368
Grocery	-0.011854	0.728335	1.000000	-0.040193	0.924641	0.205497
Frozen	0.345881	0.123994	-0.040193	1.000000	-0.131525	0.390947
Detergents_Paper	-0.101953	0.661816	0.924641	-0.131525	1.000000	0.069291
Delicatessen	0.244690	0.406368	0.205497	0.390947	0.069291	1.000000

import seaborn
seaborn.heatmap(data.corr())

Grocery 与 Detergents_Paper 相关系数为0.924641，可以看出存在着明显的相关关系。

3. 数据预处理

在这个部分，我们将通过在数据上做一个合适的缩放，并检测异常点，将数据预处理成一个更好的代表客户的形式。预处理数据是保证你在分析中能够得到显著且有意义的结果的重要环节。

3.1 特征缩放

如果数据不是正态分布的，尤其是数据的平均数和中位数相差很大的时候（表示数据非常歪斜）。这时候通常用一个非线性的缩放是很合适的，（英文原文） ，尤其是对于金融数据。一种实现这个缩放的方法是使用 Box-Cox 变换，这个方法能够计算出能够最佳减小数据倾斜的指数变换方法。一个比较简单的并且在大多数情况下都适用的方法是使用自然对数。

在下面的代码单元中，我们将实现以下功能：

• 使用 np.log 函数在数据 data 上做一个对数缩放，然后将它的副本（不改变原始data的值）赋值给 log_data。

# 使用自然对数缩放数据
log_data = np.log(data)

# 为每一对新产生的特征制作一个散射矩阵
pd.plotting.scatter_matrix(log_data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');

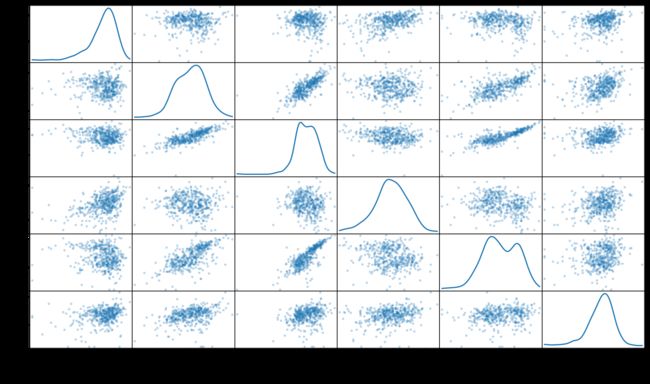
在使用了一个自然对数的缩放之后，数据的各个特征会显得更加的正态分布。

3.2 异常值检测

对于任何的分析，在数据预处理的过程中检测数据中的异常值都是非常重要的一步。异常值的出现会使得把这些值考虑进去后结果出现倾斜。这里有很多关于怎样定义什么是数据集中的异常值的经验法则。这里我们将使用 Tukey 的定义异常值的方法：一个异常阶（outlier step）被定义成1.5倍的四分位距（interquartile range，IQR）。一个数据点如果某个特征包含在该特征的 IQR 之外的特征，那么该数据点被认定为异常点。

在下面的代码单元中，我们完成下面的功能：

• 将指定特征的 25th 分位点的值分配给 Q1 。使用 np.percentile 来完成这个功能。
• 将指定特征的 75th 分位点的值分配给 Q3 。同样的，使用 np.percentile 来完成这个功能。
• 将指定特征的异常阶的计算结果赋值给 step。
• 选择性地通过将索引添加到 outliers 列表中，以移除异常值。
• 对于出现两次及以上的异常的数据点，我们将其移除，因为在一个 feature 中被认为是异常点的点，可能在其他 feature 中有着很重要的作用，甚至可能反映新的一种类型

outlier = {}
# 对于每一个特征，找到值异常高或者是异常低的数据点
for feature in log_data.keys():
    
    # 计算给定特征的Q1（数据的25th分位点）
    Q1 = np.percentile(log_data[feature],25)
    
    # 计算给定特征的Q3（数据的75th分位点）
    Q3 = np.percentile(log_data[feature],75)
    
    # 使用四分位范围计算异常阶（1.5倍的四分位距）
    step = np.percentile(log_data[feature], 75) - np.percentile(log_data[feature], 25)

    outlier.update({feature:log_data[~((log_data[feature] >= Q1 - step) & (log_data[feature] <= Q3 + step))].index.values})

#     # 显示异常点
#     print("Data points considered outliers for the feature '{}':".format(feature))
#     display(log_data[~((log_data[feature] >= Q1 - step) & (log_data[feature] <= Q3 + step))])    
    
# 查找在至少在两个特征中出现的异常点
outlier_2 = pd.Series(np.zeros(len(log_data)))
for i in range(0,len(log_data)):
    for key in outlier.keys():
        for j in outlier[key]:
            if i == j:
                outlier_2[i] = outlier_2[i]+1
                
print('至少在两个特征中出现的异常点索引：{}'.format(outlier_2[outlier_2>1].index.values))
outliers  = [outlier_2[outlier_2>1].index.values]

# 移除outliers中索引的数据点, 并储存在good_data中
good_data = log_data.drop(log_data.index[outliers]).reset_index(drop = True)

至少在两个特征中出现的异常点索引：[ 23  47  61  65  66  75  85  96  97  98 122 128 154 161 181 183 184 191 289 333 338 356 357 412 439]

4. 数据转换

在这个部分中我们将使用主成分分析（PCA）来分析批发商客户数据的内在结构。由于使用PCA在一个数据集上会计算出最大化方差的维度，我们将找出哪一个特征组合能够最好的描绘客户。

4.1 主成分分析（PCA）

既然数据被缩放到一个更加正态分布的范围中并且我们也移除了需要移除的异常点，我们现在就能够在 good_data 上使用 PCA 算法以发现数据的哪一个维度能够最大化特征的方差。除了找到这些维度，PCA 也将报告每一个维度的解释方差比（explained variance ratio）–这个数据有多少方差能够用这个单独的维度来解释。

注意 PCA 的一个组成部分（维度）能够被看做这个空间中的一个新的“特征”，但是它是原来数据中的特征构成的。

在下面的代码单元中，我们将要实现下面的功能：

• 导入 sklearn.decomposition.PCA 并且将 good_data 用 PCA 并且使用6个维度进行拟合后的结果保存到 pca 中。

import sklearn
from sklearn.decomposition import PCA

# 通过在good data上进行PCA，将其转换成6个维度
pca = PCA(n_components=6)
pca.fit(good_data)

# 生成PCA的结果图
pca_results = vs.pca_results(good_data, pca)

可以看见，在第一个主成分上主要体现的是‘Milk’、‘Grocery’和‘Detergents_Paper’的作用；而第二个主成分上主要体现了其余三个属性的作用；前两个主成分共解释了数据 68.32% 的变化，前四个主成分总共解释了数据 99.39% 的变化。

4.2 降维

当使用主成分分析的时候，一个主要的目的是减少数据的维度，这实际上降低了问题的复杂度。当然降维也是需要一定代价的：更少的维度能够表示的数据中的总方差更少。因为这个，**累计解释方差比（cumulative explained variance ratio）**对于我们确定这个问题需要多少维度非常重要。另外，如果大部分的方差都能够通过两个或者是三个维度进行表示的话，降维之后的数据能够被可视化。

在下面的代码单元中，我们将实现下面的功能：

• 将 good_data 用两个维度的PCA进行拟合，并将结果存储到 pca 中去。
• 使用 pca.transform 将 good_data 进行转换，并将结果存储在 reduced_data 中。

# 通过在good data上进行PCA，将其转换成两个维度
pca = PCA(n_components=2)
pca.fit(good_data)

# 使用上面训练的PCA将good data进行转换
reduced_data = pca.transform(good_data)

# 为降维后的数据创建一个DataFrame
reduced_data = pd.DataFrame(reduced_data, columns = ['Dimension 1', 'Dimension 2'])

4.3 双标图（Biplot）可视化

双标图是一个散点图，每个数据点的位置由它所在主成分的分数确定。坐标系是主成分（这里是 Dimension 1 和 Dimension 2）。此外，双标图还展示出初始特征在主成分上的投影。一个双标图可以帮助我们理解降维后的数据，发现主成分和初始特征之间的关系。

运行下面的代码来创建一个降维后数据的双标图。

# 可视化双标图
vs.biplot(good_data, reduced_data, pca)

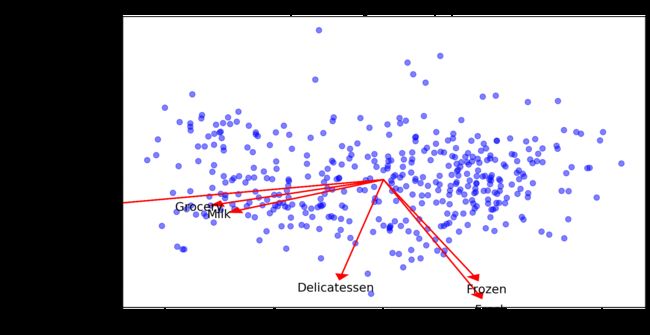
一旦我们有了原始特征的投影（红色箭头），就能更加容易的理解散点图每个数据点的相对位置。

在这个双标图中，可以看出 ‘Milk’、‘Grocery’和‘Detergents_Paper’与第一个主成分有强关联，其余初始特征与第二个主成分相关联，之前得到的 pca_results 图相符。

5. 聚类

在这个部分，我们将使用 K-Means 聚类算法以发现数据中隐藏的客户分类。然后，将从簇中恢复一些特定的关键数据点，通过将它们转换回原始的维度和规模，从而理解他们的含义。

5.1 创建聚类

针对不同情况，有些问题需要的聚类数目可能是已知的。但是在聚类数目不作为一个先验知道的情况下，我们并不能够保证某个聚类的数目对这个数据是最优的，因为我们对于数据的结构（如果存在的话）是不清楚的。但是，我们可以通过计算每一个簇中点的轮廓系数来衡量聚类的质量。数据点的轮廓系数衡量了它与分配给他的簇的相似度，这个值范围在-1（不相似）到1（相似）。平均轮廓系数为我们提供了一种简单地度量聚类质量的方法。

在接下来的代码单元中，将实现下列功能：

• 在 reduced_data 上使用一个聚类算法，并将结果赋值到 clusterer，需要设置 random_state 使得结果可以复现。
• 使用 clusterer.predict 预测 reduced_data 中的每一个点的簇，并将结果赋值到 preds。
• 使用算法的某个属性值找到聚类中心，并将它们赋值到 centers。
• 导入 sklearn.metrics.silhouette_score 包并计算 reduced_data 相对于 preds 的轮廓系数。
  • 将轮廓系数赋值给 score 并输出结果。

# 在降维后的数据上使用你选择的聚类算法
from sklearn.cluster import KMeans
clusterer = KMeans(n_clusters=2)

# 预测每一个点的簇
preds = clusterer.fit_predict(reduced_data)

# 找到聚类中心
centers = clusterer.cluster_centers_

# 计算选择的类别的平均轮廓系数（mean silhouette coefficient）
from sklearn.metrics import silhouette_score
score = silhouette_score(reduced_data, preds)
score

0.44302706341643633

5.2 聚类可视化

可视化聚类结果和聚类中心：

vs.cluster_results(reduced_data, preds, centers)

6. 数据恢复

上面的可视化图像中提供的每一个聚类都有一个中心点。这些中心（或者叫平均点）并不是数据中真实存在的点，但是是所有预测在这个簇中的数据点的平均。对于创建客户分类的问题，一个簇的中心对应于那个分类的平均用户。因为这个数据现在进行了降维并缩放到一定的范围，我们可以通过施加一个反向的转换恢复这个点所代表的用户的花费。

在下面的代码单元中，将实现下列的功能：

• 使用 pca.inverse_transform 将 centers 反向转换，并将结果存储在 log_centers 中。
• 使用 np.log 的反函数 np.exp 反向转换 log_centers 并将结果存储到 true_centers 中。

# 反向转换中心点
log_centers = pca.inverse_transform(centers)

# 对中心点做指数转换
true_centers = np.exp(log_centers)

# 显示真实的中心点
segments = ['Segment {}'.format(i) for i in range(0,len(centers))]
true_centers = pd.DataFrame(np.round(true_centers), columns = data.keys())
true_centers.index = segments
display(true_centers)

	Fresh	Milk	Grocery	Frozen	Detergents_Paper	Delicatessen
Segment 0	9564.0	2051.0	2609.0	2172.0	325.0	717.0
Segment 1	3854.0	7662.0	11498.0	914.0	4448.0	1021.0

将恢复结果与开始的特征均值可以看出：

Cluster 0 可能代表零售商用户，因为各项支出都低于平均值，符合零售店的特征；

Cluster 1 可能代表咖啡厅类客户，因为Milk、Grocery、Detergents Paper这三项支出远高于平均值，符合咖啡店的特征。

7. 利用聚类结果进行预测

对选取的样本进行类别预测：

indices = [20,200,400]

# 为选择的样本建立一个DataFrame
samples = pd.DataFrame(data.loc[indices], columns = data.keys()).reset_index(drop = True)
print("Chosen samples of wholesale customers dataset:")
display(samples)

log_samples = np.log(samples)
pca_samples = pca.transform(log_samples)
sample_preds = clusterer.predict(pca_samples)

for i, pred in enumerate(sample_preds):
    print("Sample point", i, "predicted to be in Cluster", pred)

Chosen samples of wholesale customers dataset:

	Fresh	Milk	Grocery	Frozen	Detergents_Paper	Delicatessen
0	17546	4519	4602	1066	2259	2124
1	3067	13240	23127	3941	9959	731
2	4446	906	1238	3576	153	1014

Sample point 0 predicted to be in Cluster 1
Sample point 1 predicted to be in Cluster 1
Sample point 2 predicted to be in Cluster 0