AlphaGo Zero详解

AlphaGo Zero

思考再三，决定研究一下 AlphaGo Zero，并把 AlphaGo Zero 的思想运用到五子棋 中，毕设就决定做这个。

后文：

1. 蒙特卡洛树搜索（MCTS）代码详解【python】
2. AlphaZero五子棋网络模型【python】

AlphaGo Zero 最大的亮点是：完全没有利用人类知识，就能够获得比之前版本更强大的棋力。主要的做法是:

• 利用蒙特卡洛树搜索建立一个模型提升器
• 在自我对弈过程中，利用提升器指导模型提升，模型提升又进一步提高了提升器的能力。

蒙特卡洛树搜索

要了解 AlphaGo Zero，必须先了解蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS），在次之前还要了解一些博弈论（Game theory）的基础。

博弈论

博弈论是二人或多人在平等的对局中各自利用对方的策略变换自己的对抗策略，达到取胜的目的。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。

用中国的古话说，就是要 知己知彼 方能百战不殆。

在博弈论中有一些基础概率，信息对称，零和，纳什均衡，等等。

• 信息对称（Perfect information / Fully information）是指游戏的所有信息和状态都是所有玩家都可以观察到的，因此双方的游戏策略只需要关注共同的状态即可，而信息不对称（Imperfect information / Partial information）就是玩家拥有只有自己可以观察到的状态，这样游戏决策时也需要考虑更多的因素。

• 零和（zero-sum），就是所有玩家的收益之和为零，如果我赢就是你输，没有双赢或者双输，因此游戏决策时不需要考虑合作等因素。

• 纳什平衡（Nash equilibrium）又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略，那么这个组合就被定义为纳什平衡。

而五子棋和围棋都是信息对称的，零和的游戏，在某些状态也会出现纳什均衡的情况。

极大极小值算法和阿尔法贝塔剪枝搜索算法

极小极大算法常用于零和博弈游戏中。基本思想就是假设 自己足够聪明，并且对手同样聪明 ，现在我面前有2个选择 A 和 B ，我不知道哪个选择对我更好，所以一开始我只能去猜：如果我选A对手会怎么选？如果我选了A，之后对手选了C或D，那么对我是优势还是劣势？ ……如果我选B对手会怎么选？……就这样建立一颗搜索树来遍历其中的各种情况，找到最利于自己的方案。

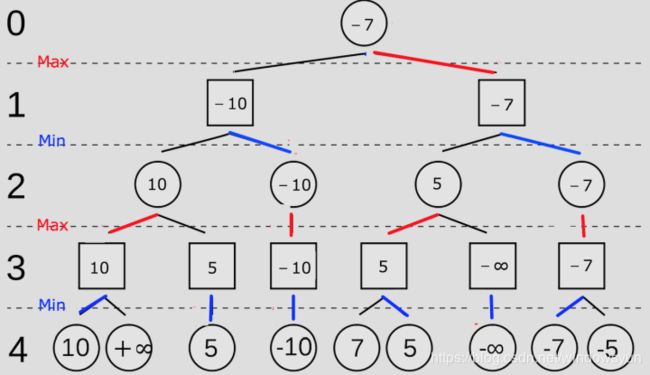
我的位置是0层，我在1层有两个选择，我要比较这两个选择哪个对我更有利，也就是选择值更大的那个。但是我要怎么知道这两个值谁大？那就再往下一层看。假设我选了1层左边的方框 ，我的对手会怎么选。现在我的对手在1层左边的方框，他要在2层的两个选择中选一个，毫无疑问他会选择评分为-10的圆，因为他会选值较小的那一个，使我的收益降低。那么对于我来说，1层左边的方框的值是 -10 而不是 10，同理右边的方框的值是-7。在这两个中我要选值最大的一个，就是-7的那一个。

关于alpha-beta剪枝：

如果当前层为取最小，如果取最小后比上一层当前最大值还小，则不需要往下搜索，因为上一层根本不会选择当前节点往下搜，还有更好的选择。

同理，如果当前层为取最大，如果取最大后比上一层当前最小值还大，则不需要往下搜索，因为上一层根本不会选择当前节点往下搜。以2层第1个圆为例，它的两个方框的值（10，5）都比旁边的圆的值（-10）要大，可以直接剪掉。

极大极小值算法在诸如象棋，黑白棋等传统游戏中取得了巨大的成功，主要原因有两个：

1. 游戏本身的探索空间相对较小（比如象棋大概是10^50），配合剪枝，开局和杀棋棋谱，非平衡树探索等优化技术，加上并行计算和Iterative Deepening，使得探索到树的深层甚至底层成为可能。
2. 搜素的最终目的就是找出对自己最有利的一步，而判断是不是有利自然需要一定的评判标准。一般我们用一个评价函数来作为标准。象棋等游戏的子有不同的强弱，并且有明确的目的性（诸如杀死对方的王），容易人工设计出或者通过机器学习得出一个良好的评价函数来正确评估一步落子所引发的后续局面。

但是围棋为什么一直搞不定？主要原因也还是那两个，

1. 围棋的棋盘是19x19，除去不能下在眼里，围棋第N步的可能下法有362-N种，探索空间要大很多(大概是10^171)。传统方法往下算几层基本就算不动了，难以正确找到最有利的下法。
2. 难以找到一个合适的评价函数。和象棋的子有强弱不同，围棋中的每个子很难给予一个明确的价值，所以对整个局面也难以做出一个正确的判断。

所以传统方法一直无法攻克围棋的难关。既然以前的路是死路一条，那么只能另辟蹊径，这条蹊径就是蒙特卡洛树探索。

蒙特卡罗方法

蒙特卡罗方法就是利用随机采样的样本值来估计真实值，理论基础是中心极限定理，样本数量越多，其平均就越趋近于真实值。

基本思想：
当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。

对于围棋，我们可以简单的用随机比赛的方式来评价某一步落子。从需要评价的那一步开始，双方随机落子，直到一局比赛结束。为了保证结果的准确性，这样的随机对局通常需要进行上万盘，记录下每一盘的结果（比如接下来的落子是黑子，那就根据中国规则记录黑子胜了或输了多少子），最后取这些结果的平均，就能得到某一步棋的评价。最后要做的就是取评价最高的一步落子作为接下来的落子。也就是说为了决定一步落子就需要程序自己进行上万局的随机对局，这对随机对局的速度也提出了一定的要求。和使用了大量围棋知识的传统方法相比，这种方法的好处显而易见，就是几乎不需要围棋的专业知识，只需通过大量的随机对局就能估计出一步棋的价值。再加上诸如All-Moves-As-First等优化方法，基于纯蒙特卡洛方法的围棋程序已经能够匹敌最强的传统围棋程序。

蒙特卡洛树探索

蒙特卡洛树探索（MCTS）也就是将以上想法融入到树搜索中，利用树结构来更加高效的进行节点值的更新和选择。

MCTS 搜索的流程一共分为四个步骤：

1. 选择：
   从根节点 R 开始，递归选择某个子节点直到达到叶子节点 L。当在一个节点s，怎么选择子节点 s∗ 呢？Tree Policy就是选择节点（落子）的策略，它的好坏直接影响搜索的好坏，所以是MCTS的一个研究重点。比如上面说的选择平均赢子数最多的走法就是一种Tree Policy。而目前广泛采用的策略有UCT。

2. 扩展：
   如果 L 节点上围棋对弈没有结束，那么创建一个子节点 C。

3. 模拟：
   根据Default Policy从扩展的位置模拟下棋到终局，计算节点 C 的质量度。完全随机落子就是一种最简单的Default Policy。当然完全随机自然是比较弱的，通过加上一些先验知识等方法改进这一部分能够更加准确的估计落子的价值，增加程序的棋力。
   Default Policy可以使用深度学习网络，比如AlphaGo Zero。

4. 反向传播：
   根据 C 的质量度，沿着传递路径反向传递，更新它爸爸爷爷祖先的质量度。

UCT & UCB

什么是UCT？什么又是UCB。
UCT的全称是UCB for Trees，UCB指的是Upper Confidence Bounds。
要解释它们，又得涉及到著名的 探索-利用困境(Explore-Exploit dilemma(EE dilemma))

多臂老虎机是一个有多个拉杆的赌博机，每一个拉杆的中奖几率是不一样的，问题是：如何在有限次数内，选择拉不同的拉杆，获得最多的收益。
假设这个老虎机有3个拉杆，最笨的方法就是每个拉杆都试几次，找到中奖概率最大的那个拉杆，然后把之后有限的游戏机会都用在这个拉杆上。
然而这个方法并不是可靠的，因为每个拉杆试1000次显然比试10次所获得的中奖概率（预估概率）更加准确。比如你试了10次，其中那个本来中奖概率不高的拉杆，有可能因为你运气好，会给你一个高概率中奖的假象。
在有限次数下，你到底是坚持在你认为中奖概率高的拉杆上投入更多的次数呢(Exploit)，还是去试试别的拉杆(Explore)呢？如何分配Explore和Exploit的次数？

针对这个问题有很多研究方法：比如ε贪婪方法(ε -Greedy method)，预估回报方法(Estimating Bandit Rewards)

ε贪婪方法就是设定一个ε值, 用来指导到底是Explore 还是 Exploit。比如将ε设定为0.1，以保证将10%的次数投入在探索（Explore）,90%的次数用于利用(Exploit)，这个方法在强化学习中非常常见。

ε贪婪方法最难的就是如何科学地选择ε，而预估回报方从另一个角度，抛弃了ε，只保留其"利用"(Exploit)的部分，用预设中奖概率"天花板"的方法来解决Explore-Exploit dilemma。首先, 将老虎机每个拉杆都设置一个比较高的预估中奖概率（比如都是100%），然后每拉一次选中的拉杆, 这个拉杆的的预估概率就会改变。比如，我第一次选择拉第一个拉杆，发现没有中奖，那这个拉杆的预估中奖概率就从100%变成了50%了。下一次Exploite选择拉杆的时候，第一个拉杆的预估概率就不是最高了，我们就去找这个时候预估概率最高的拉杆来拉，每拉一次更新一下这个拉杆的预估中奖概率。理论上来说真实概率高的拉杆其预估概率下降的速度会比真实概率低的拉杆慢，所以多试几次之后就能找到真实概率最高的那个拉杆。

我们发现上面两个方法中，某个拉杆预估的中奖概率是随着这个拉杆被拉动的次数而变化的。我们是通过预估概率作为评判标准，来决定去拉哪一个拉杆。
如果一个拉杆没有被拉到，那么这个拉杆的预估中奖概率就不会改变。然而通过直觉就可以理解，一个拉杆的预估概率的准确度是跟你总共拉了多少次拉杆（所有的拉杆被拉的次数）相关的，拉得越多预估概率就越准确。这个时候我们引入UCB概率，而不是预估概率来作为选择拉杆的评判标准。

这里涉及到的理论知识叫做Chernoff-Hoeffding bound理论。大意就是，真实概率与预估概率的差距是随着实验（拉杆）的次数成指数型下降的。
根据这个理论就可以引入UCB概率，公式如下：

其中XUCB-j是第j个拉杆的的UCB概率，Xj是这个拉杆的预估概率，N是总共实验的次数，Nj第j个拉杆被拉到的次数。

同样的这个算法只有"利用"(Exploit)的部分，将判断Exploit的标准从预估中奖概率改成UCB概率即可。

UCB的思想并不仅限运用于老虎机，在围棋中，从多种可能落子中选择一步最好的同样是类似的问题，也需要掌握好收获与探索的平衡（但是也并不完全相同 1.老虎机问题的目的是要尽量小的累积regret，而围棋只要能找到最好的那一步就够了，并不在乎探索途中的regret。2. 期望是会变动的。所以UCT对UCB进行了一定的变动，实际使用的是

也就是给偏移部分加上了一个正常数项）。而UCT就是将上述的UCB的思想运用到了树搜索中，在选择的阶段， 总是选择UCB值最大的节点，直至叶子节点L。

MCTS的出现让围棋AI的棋力得到了进步，最强的围棋程序们也都统统采用了MCTS，但是它们的棋力离顶尖棋手依然有很远的距离。

AlphaGo Zero中的MCTS

AlphaGo也是基于MCTS算法，但做了很多优化。

在AlphaGo中，使用的Tree Policy可以算是变形的UCT

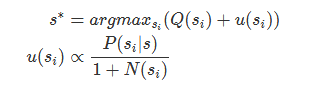
这里的s指的是一个state。从一个state做一个action，就会迁移到另一个state。Q是累积平均胜率，u则是对于Q的偏移，也就是选择让Q+u最大的一步棋。其中P(si|s)是策略网络的输出，探索刚开始时，策略网络的影响比较大，而随着探索的进行，策略网络的影响慢慢降低，偏移慢慢变小，而真正在模拟中取得更好胜率的落子会更容易被选中。N(si)是所有的模拟中(s,a)所指向节点的访问次数。

Q（s）的定义如下：

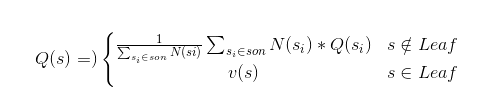这个公式的意思是：1）对于非叶子节点，质量度等于该节点所有树中已有子节点的质量度均值。2）对于叶子节点，质量度和深度学习网络估计的获胜概率 vθ(sL) 有关。

Vθ(sL)=(1−λ)vθ(sL)+λzL

vθ(sL) 是一次模拟后，那个叶的胜率（也就是反向传递回去的结果），但是这里的胜率并不简单是模拟的结果(zL)，而是综合了估值网络所给出的胜率(vθ(sL))，λ是权重系数。

有了 MCTS 的结构，就可以继续说明 MCTS 怎么做搜索的。当对手落了一子，AlphaGo 迅速读入当前盘面，将之当作搜索的根节点，展开搜索。

AlphaGo Zero 的网络结构

回顾一下AlphaGo Zero的整个流程：

它的主体是MCTS，在训练过程中，将会重复这一过程上万次。

1. 选择：
   假设当前棋面状态为xt，以xt作为数据起点，得到距今最近的本方历史7步棋面状态和对方历史8步棋面状态，分别记作xt−1，xt−2，···，xt−7和yt，yt−1，···，yt−7。并记本方执棋颜色为c，拼接在一起，记输入元st为{xt，yt，xt−1，yt−1，···，c}。并以此开始进行评估。

2. 扩展：
   使用基于深度神经网络的蒙特卡罗树搜索展开策略评估过程，经过1600次蒙特卡罗树搜索，得到当前局面xt的策略πt和参数θ下深度神经网络fθ(st)输出的策略函数pt和估值vt。

3. 模拟：
   由蒙特卡罗树搜索得到的策略πt，结合模拟退火算法，在对弈前期，增加落子位置多样性，丰富围棋数据样本。一直持续这步操作，直至棋局终了，得到最终胜负结果z。

4. 反向传播：
   根据上一阶段所得的胜负结果z与价值vt使用均方和误差，策略函数pt和蒙特卡罗树搜索的策略πt使用交叉信息熵误差，两者一起构成损失函数。同时并行反向传播至神经网络的每步输出，使深度神经网络fθ的权值得到进一步优化。

可以看到，AlphaGo Zero 的构造还是比较简单的，接下来开始研究它的一些细节。

策略价值网络具体是什么样子？如何更新？

所谓的策略价值网络，就是在给定当前局面 state 的情况下，返回当前局面下每一个可行 action 的概率以及当前局面评分的模型。通过 self-play 收集到的数据用来训练策略价值网络，而训练更新的策略价值网络也会马上被应用到MCTS中进行后面的 self-play，以生成更优质的 self-play 数据。两者相互嵌套，相互促进，就构成了整个训练的循环。

在AlphaGo Zero中，输入局面首先通过了20或40个基于卷积的残差网络模块，然后再分别接上2层或3层网络得到策略和价值输出，整个网络的层数有40多或80多层，更新非常缓慢。

策略价值网络的输入与输出

AlphaGo Zero一共使用了17个 19*19 的二值特征平面来描述当前局面，其中前16个平面描述了最近8步对应的双方player的棋子位置，最后一个平面描述当前player对应的棋子颜色，也就是先后手。他将这17个二值特征平面作为神经网络的输入，而输出有两个 policy 和 value 。在policy这一端，使用softmax非线性函数直接输出棋盘上每个位置的落子概率；在value这一端，使用tanh非线性函数直接输出 [-1,1] 之间的局面评分。

策略价值网络的训练目标

策略价值网络的输入是当前的局面描述 s ，输出是当前局面下每一个可行action的概率P 以及当前局面的评分 v ，而用来训练策略价值网络的是我们在self-play过程中收集的一系列的 (s, $\pi$, z) 数据。

我们训练的目标是让策略价值网络输出的action概率 P 更加接近MCTS输出的概率 pi ,让策略价值网络输出的局面评分 v 能更准确的预测真实的对局结果 z 。从优化的角度来说，我们是在self-play数据集上不断的最小化损失函数：

$\ell$=(z-v)²-$\pi$^TlogP + c|| $\theta$ ||² ,

第三项是用于防止过拟合的正则项。正常的话，损失函数会慢慢减小。

在训练过程中，除了观察到损失函数在慢慢减小，一般还会关注策略价值网络输出的策略（输出的落子概率分布）的entropy的变化情况。正常来讲，最开始的时候，策略网络基本上是均匀的随机输出落子的概率，所以entropy会比较大。随着训练过程的慢慢推进，策略网络会慢慢学会在不同的局面下哪些位置应该有更大的落子概率，也就是说落子概率的分布不再均匀，会有比较强的偏向，这样entropy就会变小。也正是由于策略网络输出概率的偏向，才能帮助MCTS在搜索过程中能够在更有潜力的位置进行更多的模拟，从而在比较少的模拟次数下达到比较好的性能。

self-play数据的生成和扩充

完全基于self-play来学习进化是AlphaZero的最大卖点，也是整个训练过程中最关键也是最耗时的环节。

在AlphaGo Zero版本中，需要同时保存当前最新的模型和通过评估得到的历史最优的模型，self-play数据始终由最优模型生成，用于不断训练更新当前最新的模型，然后每隔一段时间评估当前最新模型和最优模型的优劣，决定是否更新历史最优模型。而到了AlphaZero版本中，这一过程得到简化，只保存当前最新模型，self-play数据直接由当前最新模型生成，并用于训练更新自身。

一个有效的策略价值模型，需要在各种局面下都能比较准确的评估当前局面的优劣以及当前局面下各个action的相对优劣，要训练出这样的策略价值模型，就需要在self-play的过程中尽可能的覆盖到各种各样的局面。前面提到，不断使用最新的模型来生成self-play数据可能在一定程度上有助于覆盖到更多的局面，但仅靠这么一点模型的差异是不够的，所以在强化学习算法中，一般都会有特意设计的exploration的手段，这是至关重要的。

AlphaGo Zero采用的是优化的UCT算法，前面已有具体介绍。

在AlphaGo Zero论文中，每一个self-play对局的前30步，action是根据正比于MCTS根节点处每个分支的访问次数的概率采样得到的（也就是上面Self-play示意图中的 $a_t\sim {\pi }_{\mathbf{t}}$ ，有点类似于随机策略梯度方法中的探索方式），而之后的exploration则是通过直接加上Dirichlet noise的方式实现的$（P(s,a)=(1-\epsilon )P_a+\epsilon {\eta }_a$ , 有点类似于确定性策略梯度方法中的探索方式）。

围棋具有旋转和镜像翻转等价的性质，其实五子棋也具有同样的性质。在AlphaGo Zero中，这一性质被充分的利用来扩充self-play数据，以及在MCTS评估叶子节点的时候提高局面评估的可靠性。但是在AlphaZero中，因为要同时考虑国际象棋和将棋这两种不满足旋转等价性质的棋类，所以对于围棋也没有利用这个性质。而在我们的实现中，因为生成self-play数据本身就是计算的瓶颈，为了能够在算力非常弱的情况下尽快的收集数据训练模型，每一局self-play结束后，把这一局的数据进行旋转和镜像翻转，将8种等价情况的数据全部存入self-play 的 data buffer 中。这种旋转和翻转的数据扩充在一定程度上也能提高 self-play 数据的多样性和均衡性。

AlphaGo Zero的应用

AGZ算法本质上是一个最优化搜索算法，对于所有开放信息的离散的最优化问题，只要我们可以写出完美的模拟器，就可以应用AGZ算法。所谓开放信息，就像围棋象棋，斗地主不是开放信息，德扑虽然不是开放信息，但本身主要是概率问题，也可以应用。所谓离散问题，下法是一步一步的，变量是一格一格，可以有限枚举的，比如围棋361个点是可以枚举的，而股票、无人驾驶、星际争霸，则不是这类问题。Deepmind要攻克的下一个目标是星际争霸，因为它是不完全信息，连续性操作，没有完美模拟器（随机性），目前在这方面AI还是被人类完虐

所以看到AG打败人类，AGZ打败AG，就认为人工智能要打败人类了，这种观点在未来可能成立，但目前还有点危言耸听。距离真正打败人类，AGZ还差得很远。

参考资料
[1] https://zhuanlan.zhihu.com/p/32089487
[2] https://www.cnblogs.com/yifdu25/p/8303462.html
[3] http://www.algorithmdog.com/alphago-zero-notes
[4] https://blog.csdn.net/natsu1211/article/details/50986810
[5] https://www.jianshu.com/p/eecbfe8b1acb