LK光流算法及其opencv的自定义实现

折腾了一天LK光流算法，从原理、公式到代码，为了自己回顾方便以及其他读者参考，花了一些时间把今天所做的工作整理并分享出来

光流原理：

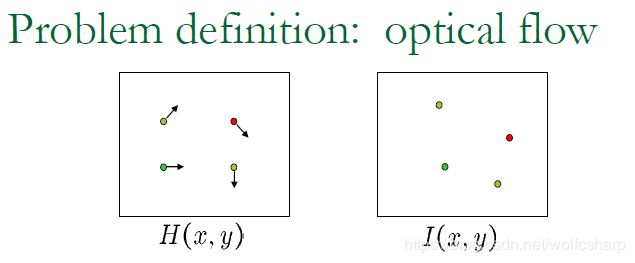
由于摄像机系统将三维场景转换为二维图像丢失了很多信息，因此要在二维图像中估计物体的运动情况就需要引入额外的信息。光流算法就是通过引入前后两帧图像的差异，从而将现实世界的运动场转换成成二维图像中的光流场。
前一帧图片表示为H(x,y)，后一帧图片表示为I(x,y)

两帧图片在x方向有u个像素的位移，在y方向有v个像素的位移

光流问题推导三大假设：

(1)brightness constancy
H(x,y)中的点与I(x,y)中目标对应的点（注意不是像素对应的点）灰度值相等
可以列出方程:
H（x，y）= I（x+u，y+v）
(2)spatial coherence
认为相邻像素运动场近似相同，运动场是空间相关的
(3)small motion
微小的运动，这是光流算法work的基础

公式推导
因为假设(3),u、v都足够小，因此可以对I(x+u,y+v)进行泰勒级数展开，并且忽略高阶项：

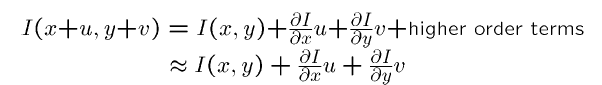
由假设1，H（x，y）= I（x+u，y+v），所以

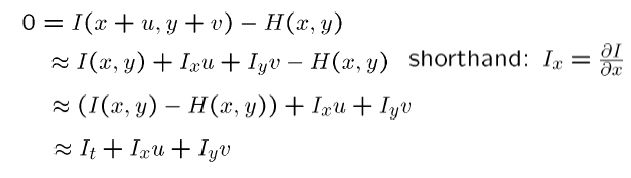
用矩阵表示即

以上方程是光流问题的基本求解方程。

Lucas-Kanade（LK）光流：

LK解法是光流基本方程解法中的一种，目前popular for稀疏光流的求解

因为假设（2），光流场是spatial coherence的，因此取一个k by k的window，这里假设k=5，于是用最小二乘法有

公式

中的求和号是对k by k的window中的所有元素进行求和

下面的问题就是矩阵求逆的解法：
这里采用伴随矩阵求逆的方法，假设矩阵A，那么矩阵A的逆为

其中|A|是矩阵的秩，A*是矩阵A的伴随矩阵
百度的伴随矩阵求法：

所以，我们的问题求解为

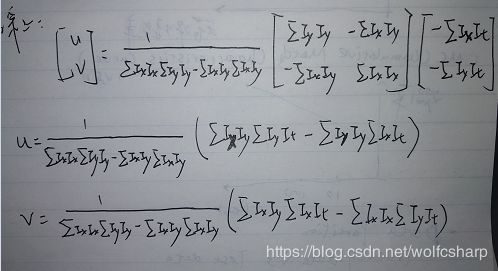
公式推导完毕，下面是算法代码，代码已经添加注释，运行环境VS2013+opencv3.4.1
测试图片包，可以点击这里下载，里面包含多个场景的多帧图片

代码：

#include 
#include "opencv2/imgproc/imgproc.hpp"
#include 
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
#include 

#define ATD at

using namespace cv;
using namespace std;

//用两帧图片获得Ix
Mat get_Ix(Mat &src1, Mat &src2)
{
	Mat Ix;
	Mat kernal = Mat::ones(2, 2, CV_64FC1);
	kernal.ATD(0, 0) = -1.0;
	kernal.ATD(1, 0) = -1.0;

	Mat dst1, dst2;
	filter2D(src1, dst1, -1, kernal);
	filter2D(src2, dst2, -1, kernal);

	Ix = dst1 + dst2;
	return Ix;
}
//用两帧图片获得Iy
Mat get_Iy(Mat &src1, Mat &src2)
{
	Mat Iy;
	Mat kernal = Mat::ones(2, 2, CV_64FC1);
	kernal.ATD(0, 0) = -1.0;
	kernal.ATD(0, 1) = -1.0;

	Mat dst1, dst2;
	filter2D(src1, dst1, -1, kernal);
	filter2D(src2, dst2, -1, kernal);

	Iy = dst1 + dst2;
	return Iy;
}
//用两帧图片获得It
Mat get_It(Mat &src1, Mat &src2)
{
	Mat It;
	Mat kernal = Mat::ones(2, 2, CV_64FC1);
	kernal = kernal.mul(-1);

	Mat dst1, dst2;
	filter2D(src1, dst1, -1, kernal);
	kernal = kernal.mul(-1);
	filter2D(src2, dst2, -1, kernal);

	It = dst1 + dst2;
	return It;
}

//取3*3的窗口，做9个值的和
Mat get_sum9(Mat &m)
{
	Mat sum9;
	Mat kernal = Mat::ones(3, 3, CV_64FC1);

	filter2D(m, sum9, -1, kernal);
	return sum9;
}

//LK算法实现
//输入:两帧图片 img1和img2
//输出:计算结果 u（x方向光流）和v（y方向光流）
void getLucasKanadeOpticalFlow(Mat &img1, Mat &img2, Mat &u, Mat &v)
{
	Mat Ix = get_Ix(img1, img2);
	Mat Iy = get_Iy(img1, img2);
	Mat It = get_It(img1, img2);
	Mat Ix2 = Ix.mul(Ix);
	Mat Iy2 = Iy.mul(Iy);
	Mat IxIy = Ix.mul(Iy);
	Mat IxIt = Ix.mul(It);
	Mat IyIt = Iy.mul(It);
	Mat Ix2_sum9 = get_sum9(Ix2);
	Mat Iy2_sum9 = get_sum9(Iy2);
	Mat IxIy_sum9 = get_sum9(IxIy);
	Mat IxIt_sum9 = get_sum9(IxIt);
	Mat IyIt_sum9 = get_sum9(IyIt);
	Mat det = (Ix2_sum9.mul(Iy2_sum9) - IxIy_sum9.mul(IxIy_sum9))*10;//A的行列式计算（二阶），这里*10是为了光流限幅
	u = IxIy_sum9.mul(IyIt_sum9) - Iy2_sum9.mul(IxIt_sum9);//算出u*det
	v = IxIy_sum9.mul(IxIt_sum9) - Ix2_sum9.mul(IyIt_sum9);//算出v*det
	divide(u, det, u);//算出u
	divide(v, det, v);//算出v
}

//在一张图片img上根据u和v画出光流场
void draw_optical_flow(Mat &img, Mat &u, Mat &v)
{
	int width = img.cols;//y
	int height = img.rows;//x

	int newi, newj;//加入光流后的新坐标
	for (int i = 0; i < height; i++)//遍历x
	{
		for (int j = 0; j < width; j++)//遍历y
		{
			newi = i + int(u.ATD(i, j));//加入光流之后的新x坐标
			newj = j + int(v.ATD(i, j));//加入光流之后的新y坐标

			if (newi >= 0 && newi = 0 && newj < width)//对边界进行限制，防止内存溢出
			{
				if ((u.ATD(i, j) + v.ATD(i, j)>2) && (u.ATD(i, j) + v.ATD(i,j)<40))//光流滤波，参数2-40
				{
					circle(img, Point(newj, newi), 1, Scalar(0, 0, 255));//在新坐标点画圆，半径为1，颜色红色
					line(img, Point(j, i), Point(newj, newi), Scalar(0, 0,255));//两个点之间画线，颜色红色
				}
			}

		}
	}
}
void main()
{
	//用前后两帧图片做测试
	Mat img1 = imread("frame08.png", 0);//参数：图片名称，0以灰度方式读入
	Mat img2 = imread("frame09.png", 0);

	img1.convertTo(img1, CV_64FC1, 1.0/255, 0);//如果用imshow()的话，需要写成1.0/255
	img2.convertTo(img2, CV_64FC1, 1.0/255, 0);//如果用imwrite()的话，需要写成1， 并不影响实际光流计算结果

	Mat u = Mat::zeros(img1.rows, img1.cols, CV_64FC1);
	Mat v = Mat::zeros(img1.rows, img1.cols, CV_64FC1);
	getLucasKanadeOpticalFlow(img1, img2, u, v);
	imshow("u", u);
	imshow("v", v);

	Mat img = imread("frame08.png");//重新读入彩色图片
	draw_optical_flow(img, u, v);//在这张图片上画出光流结果
	imshow("optical_flowflow", img);
	imwrite("optical_flow.jpg",img);
	waitKey(0);
}

注意，为了减少计算量，这里取用的窗口是3*3的，实际速度还可以
LK光流运行结果：