人工神经网络(ANN)模型简介

ANN简介

作为深度学习的基础，神经网络模型发挥着很重要的作用。

我们来看一下ANN的定义：

神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界物体所作出交互反应。

我们知道，生物神经网络的简单单元由生物神经元组成，那么在ANN模型中，简单单元由什么组成呢？

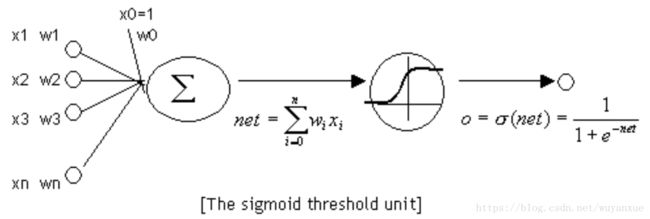
在经典ANN模型中，简单单元，即M-P神经元模型。我们知道感知机和Logistic回归都是线性分类模型，它们的不同点在于分类函数的选取是不一样的。
我们令 z=wTx z = w T x 。感知机的分类决策函数： f(x)=g(z)=sign(z) f ( x ) = g ( z ) = s i g n ( z )
其中 sign(⋅) s i g n ( ⋅ ) 为阶跃函数： sign(z)=1 ifz≥0 else 1 s i g n ( z ) = 1   i f z ≥ 0   e l s e   1
Logistic回归的分类决策函数则是Sigmoid函数： f(x)=g(z)=11+e−z f ( x ) = g ( z ) = 1 1 + e − z ，它表示的是将样本分类成正例和负例的几率比。也是一个阶跃函数的替代函数。

具体地请参考我的博客
https://blog.csdn.net/wuyanxue/article/details/80205582

典型的M-P神经元模型的输入与输出和Logistic回归一样，不过在这里Sigmoid是作为激活函数而存在的。也就是说，Sigmoid表示的只是一个神经元的输出，不代表整个ANN的输出。一张图形象地表示该MP神经元：

ANN是什么？

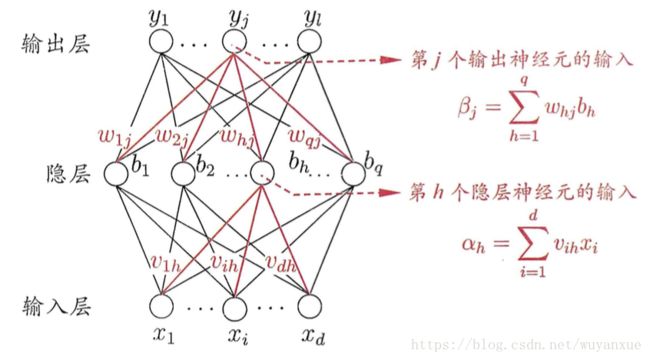
我们知道生物神经网络是由非常多的生物神经元连接而成。类似地，ANN也是由多个神经元模型按照一定的规则连接构成。下图展示了一个全连接（Full Connected）神经网络（FNN）：

我们可以发现FNN具有以下特点：
1. 神经元按照层来布局。如上图，最左边称为输入层（Input layer），中间称为隐藏层（Hidden layer），最右边称为输出层（Output layer）
2. 同一层的神经元没有连接。
3. 第N层的每个神经元都第N-1层的所有神经元连接（这就是Full connected的含义），第N-1层神经元的输出就是第N层神经元的输入。
4. 每个神经元的连接都具有一个权值。注意到，这里的 X=(x1,x2,x3) X = ( x 1 , x 2 , x 3 ) 表示的是一个输入向量， Y=(y1,y2) Y = ( y 1 , y 2 ) 表示的是输出向量。
5. 另外，隐藏层可以是多层。

不失一般性，假设一个训练样本为 x=(x1,…,xd)∈Rd x = ( x 1 , … , x d ) ∈ R d , 对应的输出向量为 y=(y1,…,yl) y = ( y 1 , … , y l ) ， l l 为类别个数，即输出向量是类别的独热编码。隐藏层第h个节点的输入权重为 v1h,⋯,vdh v 1 h , ⋯ , v d h ，对应的偏移量为 γh γ h 。第j个输出层节点的输入权重为 w1j,…,wqj w 1 j , … , w q j ，对应的偏移量为 θj θ j 。 q q 为隐藏层节点个数。

令 f(z)=11+e−z f ( z ) = 1 1 + e − z 为sigmoid函数

如图所示，第j个输出神经元的输入是
βj=∑qh=1whjbh β j = ∑ h = 1 q w h j b h
第j个输出神经元的输出是
yj=f(βj+θj) y j = f ( β j + θ j )
第h个隐层神经元的输入是
αh=∑di=1vihxi α h = ∑ i = 1 d v i h x i
第h个隐层神经元的输出是
bh=f(αh+γh) b h = f ( α h + γ h )

现在，我们知道了在FNN中的每个神经元输入输出的计算方法。那么如何来训练呢？

FNN的训练算法-误差逆传播（Back Propagation, BP）算法

再来看这个图，这里的输出对应的有三个分量，这里假设的是一个三类别分类问题。所以在训练的时候，类别属性要进行one hot coding。

对一个训练样本 (x,y)∈Rd×Rl ( x , y ) ∈ R d × R l , l l 为类别个数，假设神经网络的输出为 ŷ =(ŷ 1,…,ŷ l) y ^ = ( y ^ 1 , … , y ^ l ) 。
即 ŷ j=f(βj+θj) y ^ j = f ( β j + θ j )
那么网络在输出节点上的均方误差为
E=12∑lj=1(yj−ŷ j)2 E = 1 2 ∑ j = 1 l ( y j − y ^ j ) 2
BP算法的本质就是梯度下降，在训练神经网络的时候，任意参数的迭代更新公式为：
v←v+Δv v ← v + Δ v
1. 隐藏层到输出层的权值 whj w h j 的更新过程如下:
Δwhj=−η∂∂whjE Δ w h j = − η ∂ ∂ w h j E
我们知道， whj w h j 构成了 βj β j , βj β j 影响了 ŷ j y ^ j , 最终 ŷ j y ^ j 影响了 E E
因此由链式法则可知：
Δwhj=−η∂βj∂whj∂ŷ j∂βj∂E∂ŷ j Δ w h j = − η ∂ β j ∂ w h j ∂ y ^ j ∂ β j ∂ E ∂ y ^ j
∂βj∂whj=bh ∂ β j ∂ w h j = b h
∂ŷ j∂βj=ŷ j(1−ŷ j) ∂ y ^ j ∂ β j = y ^ j ( 1 − y ^ j )
∂E∂ŷ j=(ŷ j−yj) ∂ E ∂ y ^ j = ( y ^ j − y j )
因此 Δwhj=ηŷ j(1−ŷ j)(yj−ŷ j)bh Δ w h j = η y ^ j ( 1 − y ^ j ) ( y j − y ^ j ) b h
2. 输出层的阈值 θj θ j 更新如下：
Δθj=−η∂∂θjE=−η∂ŷ j∂θj∂E∂ŷ j Δ θ j = − η ∂ ∂ θ j E = − η ∂ y ^ j ∂ θ j ∂ E ∂ y ^ j
∂ŷ j∂θj=ŷ j(1−ŷ j) ∂ y ^ j ∂ θ j = y ^ j ( 1 − y ^ j )
Δθj=ηŷ j(1−ŷ j)(yj−ŷ j) Δ θ j = η y ^ j ( 1 − y ^ j ) ( y j − y ^ j )

这时，误差被逆向传播到隐藏层。同理可以计算， Δvih Δ v i h 和 γh γ h 。

总结一下，标准BP算法的伪代码如下：

我们看到，上述算法是针对每一个样本都会进行一次参数更新，类似的可以推导出累积BP算法，即对所有训练集的累积误差极小化。这两种方法类似于随机梯度下降和标准梯度下降的区别。而读取训练集一遍往往被称为一轮学习(one epoch)。