群论基本概念学习
1.群的定义是很容易理解的,这里就不赘述了。关键点是封闭性,结合律,单位元,逆元。
2.群元素的数目叫做群的阶
3.理解群的最基本的出发点的是群的乘法表
写群乘法表的关键是重排定理,即乘法表每一行每一列所有元素都要出现且只出现一次。有了这个定理,就可以很快确定乘法表
根据重排定理,可以唯一写出二阶群和三阶群的乘法表
群元的阶是指群元素自乘n次等于单位元,称为群元的阶是n
生成元:由群中最小的群元素通过乘法可以生成整个群。则称为生成元。
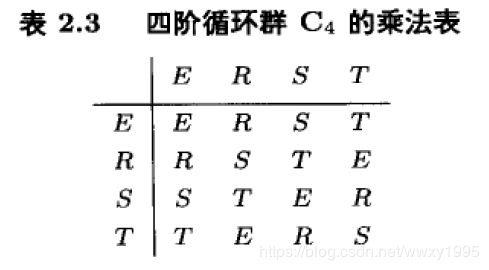
有了生成元的概念,就能很方便的研究四阶群,考虑四阶群中,如果群元素的阶为4,那么就是四阶循环群,令R=A,S=A^2,T=A^3,那么可以很快给出群表
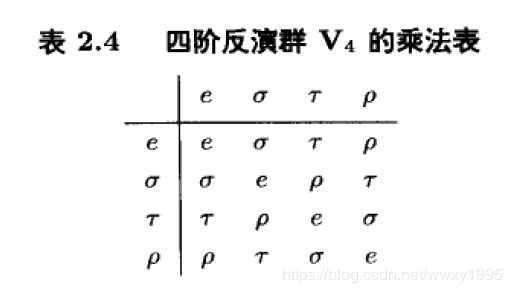
实际上4阶段群并不是只有C4,注意4阶群不可能有阶为3的元素,因为这样与重排定理相矛盾,所以所有元素的阶都为2
这样,对角线上的元素都是e,那么在用重排定理就能给出群表
从几何意义可以分析出,正三角形对称群D3由E,D,F三个C3群元素,和A,B,C三个二阶群元构成。这个乘法表写起来稍微有一点复杂
4.子群是一个很好理解的概念
D3群由子群{E,A},{E,B},{E,C}, {E,D,F}
关于子群的阶有一个很强的定理,就是子群的阶数g必然是群的阶数G的因子。
D3群的子群只可能是1,2,3阶群。
5.陪集略难理解
取一个子群,然后用群内任意一元素,左乘和右乘这个子群,得到左陪集或右陪集
以D3群为例子{E,D,F}的陪集可以算出是{A,B,C}
{E,A}关于B的是左培是{B,D},右培集是{B,F}
陪集有一个很强的定理,是陪集SX和SY要么完全相同,要么完全不同,S为子群,X为任意群元。
6.共轭元与类
B=XAX^(-1),这里A,B,X都为G的群元素,且X是某一个群元
可以证明共轭是相互的,所有共轭的元素组成一类
类有以下性质
(1)E自成一类
(2)类相互独立,没有公共元素
(3)除E外,类都不是群,因为都没有E。看前两个性质
(4)矩阵群同类元具有相同的迹,因为是相似变换。
例子,将D3群分类,首先E是一类。可以验证,D,F成一类,A,B,C成一类,这个用群表示的相似矩阵是很容易理解的,D,F都是转动60°,A,B,C都是轴对称反演,其群表示的矩阵应该相似。